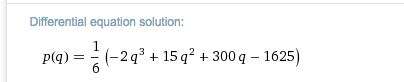Recall that the fundamental theorem of calculus states that if \(F(x)\) is a function with its derivative equal to \(f(x)\) on the region \(a \leq x \leq b\text{,}\) then \(\int_a^b f(x)\,dx=F(b)-F(a)\text{.}\) We say \(\int_a^b f(x)\,dx\) is the definite integral of \(f(x)\) from \(a\) to \(b\text{.}\) If \(f(x)\) is a derivative of \(F(x)\text{,}\) then \(F(x)\) is an anti-derivative of \(f(x)\text{,}\) and any anti-derivative of \(f(x)\) has the form \(F(x) + c\text{,}\) for some constant \(c\text{.}\) We use the symbol \(\int f(x)\,dx\text{,}\) without limits of integration, for the indefinite integral.
In
Section 7.1 we looked at approximating definite integrals with a Riemann sum that added up the area of a bunch of rectangles. In
Section 7.2 we saw that the fundamental theorem of calculus lets us use an antiderivative or indefinite integral to evaluate a definite integral. In
Section 7.3–7.4 we saw how to compute indefinite integrals by hand for a limited number of functions. In this section, we will look at how to use computer software at a web site to find antiderivatives.
We start with Wolfram|Alpha, available at
http://www.wolframalpha.com. We can give Wolfram|Alpha the question we want solved in plain English. In our case we would like to find the antiderivative of
\(x^n\) with respect to
\(x\text{.}\)
The Alpha provides an answer.
Note that the response tells us the question the Wolfram|Alpha is answering. That helps us check that we have been properly understood. We may find it useful to give a formula without the extra words.
The interface is fairly robust. It understands the convention that the variable for math problems is typically \(x\text{,}\) so it will generally guess that \(x\) is our variable if we don’t specify the variable with respect to which we are integrating.
It is worth noting that Wolfram|Alpha is connected with Mathematica, so it will understand questions in Mathematica syntax. On the right side to the screen there is a link for related links. In particular, there will be a link for the related command in Mathematica.
Following that link gives more information on the syntax of the Mathematica command. We generally don’t need to know the syntax, but it is useful if we want to use specific options.
We should note that Wolfram|Alpha will easily find antiderivatives that we would find very hard to do or beyond the scope of this class.
The output also has a link for showing steps on complicated problems.
In
Chapter 4, we found a derivative calculator. Similarly we can find an integral calculator (
http://www.integral-calculator.com/) that will show steps. For problems of at the level of difficulty we have been doing, Wolfram|Alpha also produces plots of the integral.
Subsection 7.5.1 Definite integrals
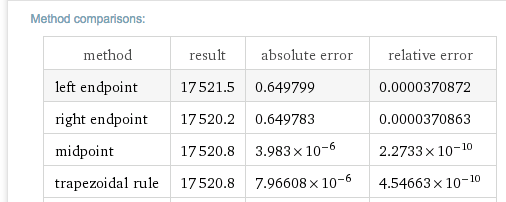
One of the reasons we wanted to find antiderivatives was to be able to use them to evaluate definite integrals. We can ask Wolfram|Alpha for the definite integral directly. In that case, Wolfram|Alpha will give the numeric answer and will also produce the relevant graph. (Symbolab will also do definite integrals.)
This is particularly useful when finding the antiderivative is beyond the scope of this course. Consider for example if we want to find the area under a portion of a curve that has the shape of a normal curve.
Another example when we can easily set up integrals we cannot solve by hand occurs when we are trying to find the current value of a revenue stream. A value, \(V\text{,}\) that we get \(t\) years in the future, has a present value of \(V \exp(-r t)\) where \(r\) is an investment return rate. Thus the current value of a revenue stream, \(V(t)\text{,}\) from time \(a\) to time \(b\text{,}\) is \(\int_a^b V(t)*e^{(-r*t)} dt\text{.}\) However we only have a rule for finding the antiderivative when \(V(t)\) is either a constant or exponential function. With a CAS program it is straightforward to compute such integrals for a broad range of value stream functions.
If you are going to use Wolfram|Alpha in doing work, you should realize that the terms of use of the site require you to appropriately cite Wolfram|Alpha. (This is standard academic procedure.) Your citation should include that date that you got your answer from the site. The results above were obtained on Feb 29, 2012.
In business situations, we are rarely asked to simply find an integral. Instead, finding an integral is generally part of a larger problem. Thus we often use CAS for part of a problem.
Subsection 7.5.2 Initial value problems
We often want to choose a particular antiderivative of a function. We typically do this when we have the value of the antiderivative for some value. We simply plug that value into the general antiderivative and solve for \(C\text{.}\)
Example 7.5.1. Finding the antiderivative, then the constant.
The rate of change profit with respect to quantity is given by \(P'(q)=-q^2+5q+50\) and the break-even point occurs when \(q=5\text{.}\) Find the formula for profit as a function of \(q\text{.}\) Find the maximum profit.
Solution.
We can do this by putting together things we have already done. First we use Wolfram|Alpha to find an antiderivative.
Thus we know \(P(q)=\frac{1q^3}{3}+\frac{5q^2}{2}+50q+C\) for some constant \(C\text{.}\) We also know \(P(5)=0\text{.}\)
Thus, \(0=P(5)=\frac{5^3}{3}+\frac{5*5^2}{2}+50*5+C\text{,}\) or \(--C=\frac{5^3}{3}+\frac{5*5^2}{2}+50*5\text{.}\)
Using Excel, we now plug the function, without the \(C\text{,}\) into Excel and evaluate at \(q=5\text{.}\)
We make \(C\) the negative of our answer and modify our function accordingly. We now use solver to maximize the function.
Thus the maximum profit is $145.83, and it occurs when \(q=10\text{.}\)
Example 7.5.2. The previous example in one step.
The rate of change profit with respect to quantity is given by \(P' (q)=-q^2+5q+50\) and the break-even point occurs when \(q=5\text{.}\) Find the formula for profit as a function of \(q\text{.}\) Find the maximum profit.
Solution.
We can also do this with Wolfram|Alpha bysetting up the boundary value problem. We give the alpha bot the derivative we want integrated and the fixed value of the original function. (Notice that the answer does not include a \(+C\text{,}\) since we have computed a particular constant.)
We then ask Alpha to maximize the function.
This gives the same answer of $145.83.
This first example could easily have been done by hand. We can repeat the process with an example that could not be easily been by hand.
Example 7.5.3. A more complicated initial value problem.
The rate of change of profit with respect to quantity is given by \(P' (q)=q^2 \exp(-q/10)-q/10\) and a break-even point occurs when \(q = 5\text{.}\) Find the formula for profit as a function of \(q\text{.}\) Find the maximum profit.
Solution.
In structure, this example is very similar to the first example. However, where in the first example, the function would have been easy to do by hand, in this case, the problem is very hard to do by hand. We use Wolfram/Alpha to find the antiderivative.
\begin{equation*}
P(q) = \exp(-q/10)*(-10*q^2-200*q-2000)-q^2/20+C\text{.}
\end{equation*}
We then use Excel to find \(C\text{,}\) noting that if we use \(P(q)\) without the \(C\text{,}\) then \(C\) is the value of \(-P(5) = 1972.474\text{.}\)
We plug in 5 and note \(P(5) = 0 = C-1972.474\text{,}\) thus \(C = 1972.474\text{.}\) We use solver to maximize and find the maximum profit of $1675.17 occurs at \(q=64.72775\text{.}\)