9 Tabular Data

9.1 Test of proportions

Many times, we are interested in estimating and inference on the proportion \(p\) in a Bernoulli trial. For example, we may be interested in the true proportion of times that a die shows a 6 when rolled, or the proportion of voters in a population who favor a particular candidate. In order to do this, we will run \(n\) trials of the experiment and count the number of times that the event in question occurs, which we denote by \(x\). For example, we could toss the die \(n = 100\) times and count the number of times that a 6 occurs, or sample \(n = 500\) voters (from a large population) and ask them whether they prefer a particular candidate. Note that in the second case, this is not formally a Bernoulli trial unless you allow the possibility of asking the same person twice; however, if the population is large, then it is approximately repeated Bernoulli trials.

The natural estimator for the true proportion \(p\) is given by \[ \hat p = \frac xn \] However, we would like to be able to form confidence intervals and to do hypothesis testing with regards to \(p\). Here, we present the theory associated with performing exact binomial hypothesis tests using binom.test, as well as prop.test, which uses the normal approximation.

9.1.1 Hypothesis Testing

Suppose that you have null hypothesis \(H_0: p = p_0\) and alternative \(H_a: p \not= p_0\). You run \(n\) trials and obtain \(x\) successes, so your estimate for \(p\) is given by \(\hat p = x/n\). Presumably, \(\hat p\) is not exactly equal to \(p_0\), and you wish to determine the probability of obtaining an estimate that far away from \(p_0\) or further. Formally, we are going to add the probabilities of all outcomes that are no more likely than the outcome that was obtained, since if we are going to reject when we obtain \(x\) successes, we would also reject if we obtain a number of successes that was even less likely to occur.

Example (Using binom.test) Suppose you wish to test \(H_0: p = 0.4\) versus \(H_a: p \not= 0.4\). You do 100 trials and obtain 50 successes.The probability of getting exactly 50 successes is dbinom(50, 100, 0.4), or 0.01034. Anything more than 50 successes is less likely under the null hypothesis, so we would add all of those to get part of our \(p\)-value. To determine which values we add for successes less than 40, we look for all outcomes that have probability of occurring (under the null hypothesis) less than 0.01034. Namely, those are the outcomes between 0 and 30, since dbinom(30, 100, 0.4) is 0.01001, while dbinom(31, 100, .04) is .015. See also the following figure, where the dashed red line indicates the likelihood of observing exactly 50 successes. We sum all of the probabilities that are below the dashed red line. (Note that the x-axis has been truncated.)

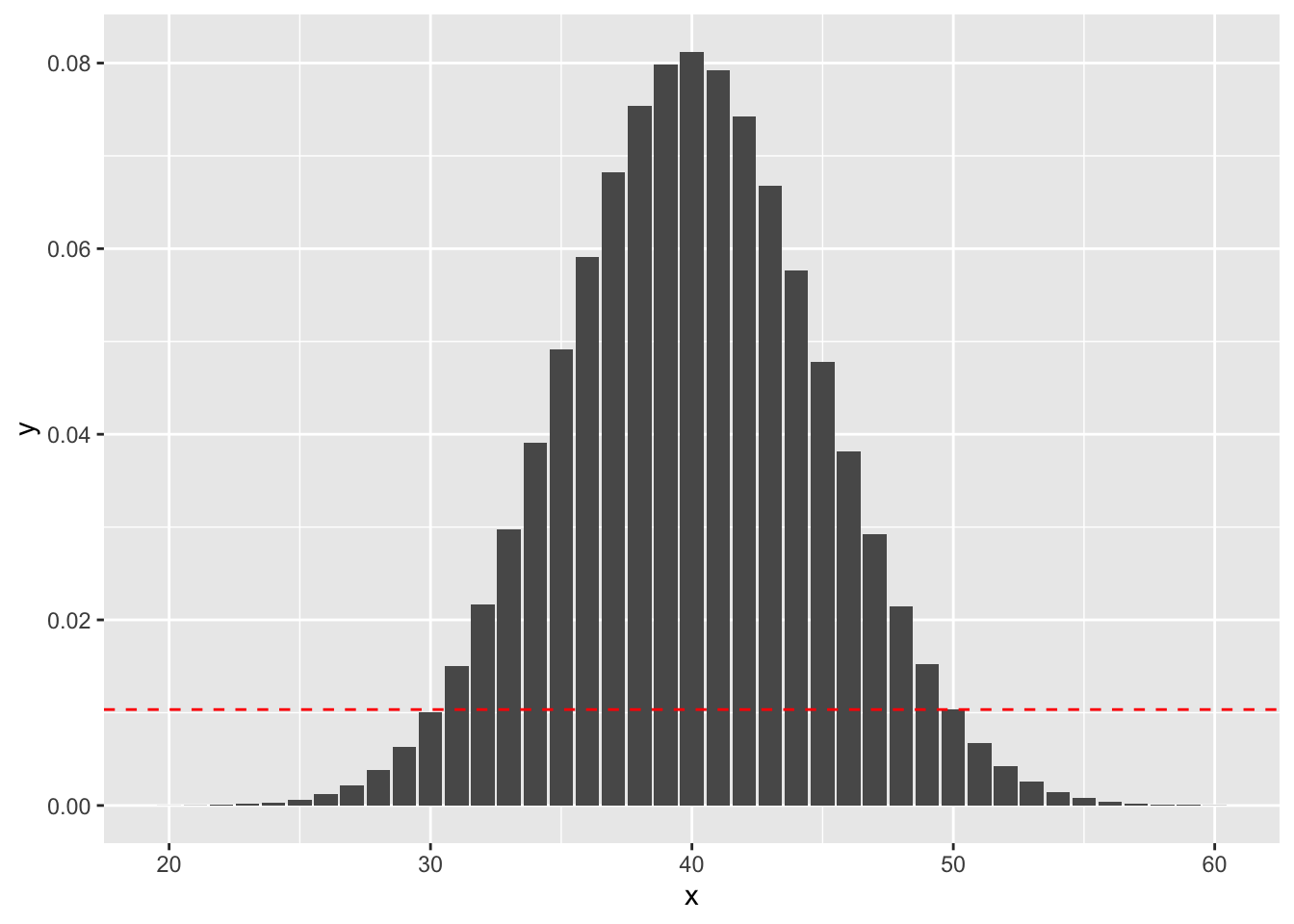
So, the \(p\)-value would be \[ P(X \le 30) + P(X \ge 50) \] where \(X\sim\) Binomial(n = 100, p = 0.4).

sum(dbinom(x = 50:100, size = 100, prob = .4)) + 
  sum(dbinom(x = 0:30, size = 100, prob = .4))

## [1] 0.05188202

On the other hand, if we obtained 30 successes, the \(p\)-value would sum the probabilities that are less than observing exactly 30 successes, as indicated by this plot:

ggplot(plotData, aes(x, y)) + geom_bar(stat = "identity") +
  geom_abline(slope = 0, intercept = dbinom(30, 100, 0.4), linetype = "dashed", color = "red")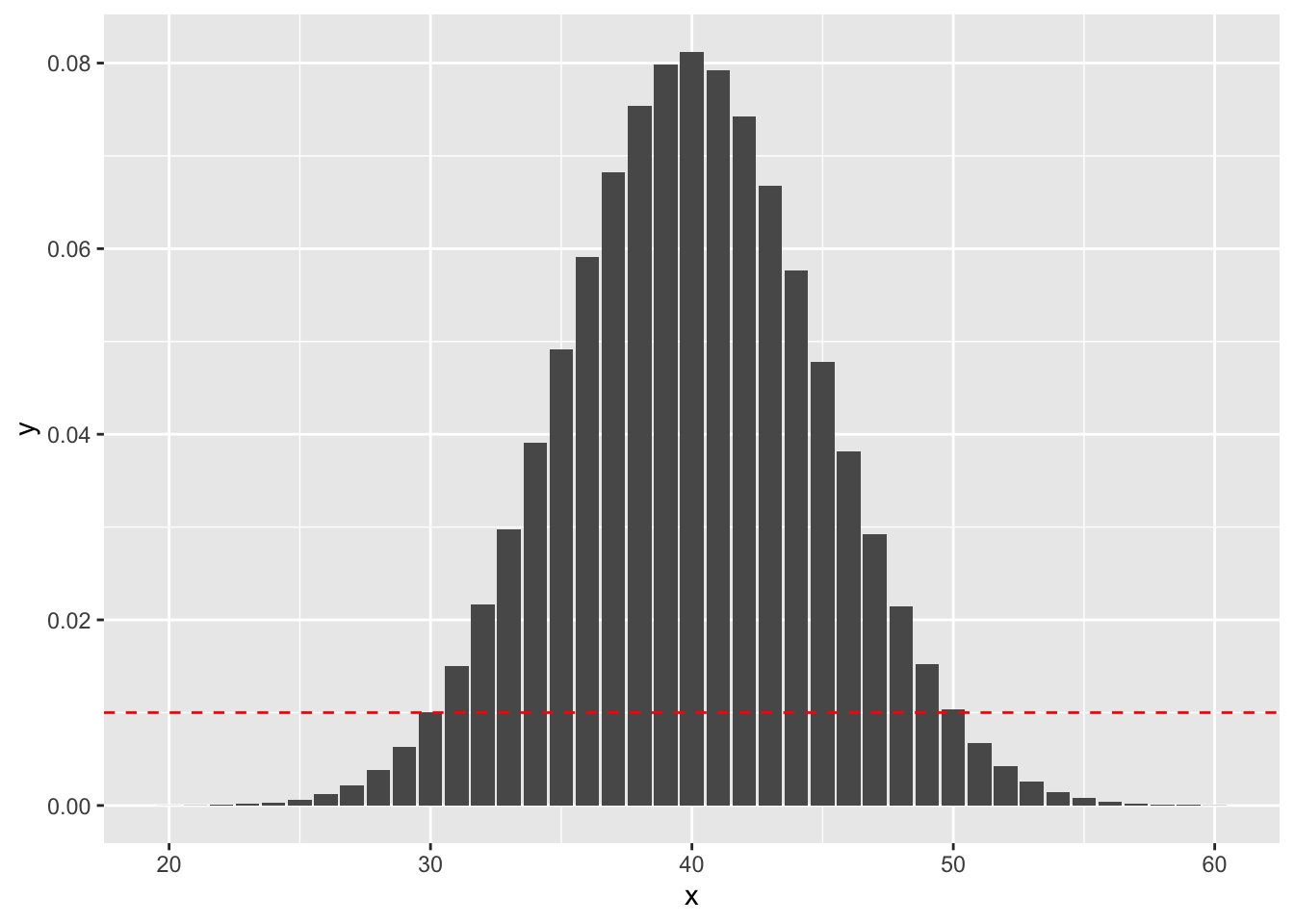

sum(dbinom(x = 51:100, size = 100, prob = .4)) + 
  sum(dbinom(x = 0:30, size = 100, prob = .4))

## [1] 0.04154451

because the outcomes that are less likely under the null hypothesis than obtaining 30 successes are (1) getting fewer than 30 successes, and (2) getting 51 or more successes. Indeed, dbinom(51, 100, 0.4) is 0.0068.

R will make these computations for us, naturally, in the following way.

binom.test(x = 50, n = 100, p = .4)

## 
##  Exact binomial test
## 
## data:  50 and 100
## number of successes = 50, number of trials = 100, p-value =
## 0.05188
## alternative hypothesis: true probability of success is not equal to 0.4
## 95 percent confidence interval:
##  0.3983211 0.6016789
## sample estimates:
## probability of success 
##                    0.5

binom.test(x = 30, n = 100, p = .4)

## 
##  Exact binomial test
## 
## data:  30 and 100
## number of successes = 30, number of trials = 100, p-value =
## 0.04154
## alternative hypothesis: true probability of success is not equal to 0.4
## 95 percent confidence interval:
##  0.2124064 0.3998147
## sample estimates:
## probability of success 
##                    0.3

Example (Using prop.test) When \(n\) is large and \(p\) isn’t too close to 0 or 1, binomial random variables with \(n\) trials and probability of success \(p\) can be approximated by normal random variables with mean \(np\) and standard deviation \(\sqrt{np(1 - p)}\). This can be used to get approximate \(p\)-values associated with the hypothesis test \(H_0: p = p_0\) versus \(H_a: p\not= p_0\).

We consider again the example that in 100 trials, you obtain 50 successes when testing \(H_0: p = 0.4\) versus \(H_a: p\not= 0.4\). Let \(X\) be a binomial random variable with \(n = 100\) and \(p = 0.4\). We approximate \(X\) by a normal rv \(N\) with mean \(np = 40\) and standard deviation \(\sqrt{np(1 - p)} = 4.89879\). As before, we need to compute the probability under \(H_0\) of obtaining an outcome that is as likely or less likely than obtaining 50 successes. However, in this case, we are using the normal approximation, which is symmetric about its mean. Therefore, the \(p\)-value would be \[ P(N \ge 50) + P(N \le 30) \] We compute this via

pnorm(50, 40, 4.89879, lower.tail = FALSE) + pnorm(30, 40, 4.89879)

## [1] 0.04121899

The built in R function for this is prop.test, as follows:

prop.test(x = 50, n = 100, p = 0.4, correct = FALSE)

## 
##  1-sample proportions test without continuity correction
## 
## data:  50 out of 100, null probability 0.4
## X-squared = 4.1667, df = 1, p-value = 0.04123
## alternative hypothesis: true p is not equal to 0.4
## 95 percent confidence interval:
##  0.4038315 0.5961685
## sample estimates:
##   p 
## 0.5

Note that to get the same answer as we did in our calculations, we need to set correct = FALSE. It is typically desirable to set correct = TRUE, which performs a continuity correction. The basic idea is that \(N\) is a continuous rv, so when \(N = 39.9\), for example, we need to decide what integer value that should be associated with. Continuity corrections do this in a way that gives more accurate approximations to the underlying binomial rv (but not necessarily closer to using binom.test).

prop.test(x = 50, n = 100, p =  .4)

## 
##  1-sample proportions test with continuity correction
## 
## data:  50 out of 100, null probability 0.4
## X-squared = 3.7604, df = 1, p-value = 0.05248
## alternative hypothesis: true p is not equal to 0.4
## 95 percent confidence interval:
##  0.3990211 0.6009789
## sample estimates:
##   p 
## 0.5

9.1.2 Confidence Intervals

Confidence intervals for \(p\) can be read off of the output of the binom.test or prop.test. They again will give slightly different answers. We illustrate the technique using prop.test.

Example The Economist/YouGov poll leading up to the 2016 presidential election sampled 3669 likely voters and found that 1798 intended to vote for Clinton. Assuming that this is a random sample from all likely voters, find a 99% confidence interval for \(p\), the true proportion of likely voters who intended to vote for Clinton at the time of the poll.

prop.test(x = 1798, n = 3699, conf.level = 0.99)

## 
##  1-sample proportions test with continuity correction
## 
## data:  1798 out of 3699, null probability 0.5
## X-squared = 2.8127, df = 1, p-value = 0.09352
## alternative hypothesis: true p is not equal to 0.5
## 99 percent confidence interval:
##  0.4648186 0.5073862
## sample estimates:
##         p 
## 0.4860773

Thus, we see that we are 99% confident that the true proportion of likely Clinton voters was between .4648186 and .5073862. (Note that in fact, 48.2% of the true voters did vote for Clinton, which does fall in the 99% confidence interval range.)

9.2 Multinomial Experiments

Many experiments involve counting outcomes in various categories. One example of that is in the previous section, where there were two categories (success and failure) and we were interested in hypothesis testing and confidence intervals related to the proportion os successes. For example, suppose that a phone case comes in three possible colors. We might be interested in whether all three colors are equally preferred by customers, or whether customers have a favorite color. Suppose that 41 people prefer blue, 32 people prefer red, and 27 people prefer white. The question under consideration is whether all three colors are equally preferred. We present here several approaches to this problem.

One way to proceed would be to assign a measure of deviance from “equally preferred.” We could for example sum the absolute deviations away from what would be expected under the null hypothesis that each color is equally preferred, and simulate the probability that we get data that is as much evidence or more evidence against \(H_0\) as what was observed. Here are the details:

expected_colors <- c(100, 100, 100)/3
dat <- c(41, 32, 27)
sum(abs(dat -expected_colors))

## [1] 15.33333

This measure of deviation from expected is 15.333. Now, let’s see how unlikely it is to get such a high measure of deviation from what is expected.

sim_data <- replicate(10000, {
  simulated_colors <- rmultinom(n = 1, size = 100, prob = c(1/3, 1/3, 1/3))
  sum(abs(expected_colors - simulated_colors))
})
mean(sim_data >= 15.33333)

## [1] 0.2593

This shows that about 25% of the time, we will get data this far from what is expected (or further). Therefore, the \(p\)-value of this experiment is approximately \(p = 0.25\), and we fail to reject \(H_0\), and conclude that there is not sufficient evidence to conclude that there is a difference in preference of colors of phone cases.

There are a couple of ways to improve on the above ad hoc method. First, it would be better to sum the probabilities of all outcomes that are less likely than what was observed (under the assumption of \(H_0\)). In order to this, we use the multinomial.test function in the EMT library.

library(EMT)
multinomial.test(dat, prob = c(1/3, 1/3, 1/3))

## 
##  Exact Multinomial Test, distance measure: p
## 
##     Events    pObs    p.value
##       5151  0.0019      0.237

Here, we get that the \(p\)-value is 0.237, which doesn’t change our conclusion that we fail to reject \(H_0\).

Another way is to use Pearson’s \(\chi^2\) statistic as a measure of deviation from expected. Pearson’s statistic is \[ \sum_{j = 1}^k \frac{(E[X_i] - X_i)^2}{E[X_i]} \] where \(X_1, \ldots, X_k\) are the observed counts in the \(k\) categories. Using this measure of deviance, we first compute the deviance from expected for the observed data.

expected_colors <- c(100, 100, 100)/3
dat <- c(41, 32, 27)
sum(abs(dat -expected_colors)^2/expected_colors)

## [1] 3.02

We get 3.02 as the deviance from expected. The probability of observing data with deivance from expected (by this measure) of at least 3.02 is estimated via:

sim_data <- replicate(10000, {
  simulated_colors <- rmultinom(n = 1, size = 100, prob = c(1/3, 1/3, 1/3))
  sum(abs(simulated_colors - expected_colors)^2/expected_colors)
})
mean(sim_data >= 3.02)

## [1] 0.2208

And we obtain a \(p\)-value of about 0.22. There are two ways to get this value using R:

EMT::multinomial.test(dat, prob = c(1/3, 1/3, 1/3), useChisq = T)

## 
##  Exact Multinomial Test, distance measure: chisquare
## 
##     Events    chi2Obs    p.value
##       5151       3.02     0.2258

The true probability of getting deviance at least 3.02, as measured by Pearsons \(\chi^2\) statistic, is 22.58%.

chisq.test(dat)

## 
##  Chi-squared test for given probabilities
## 
## data:  dat
## X-squared = 3.02, df = 2, p-value = 0.2209

This gives an estimate of the probability. It can be shown that the test statistic is approximately a \(\chi^2\) random variable with 2 degrees of freedom, and we compute

pchisq(3.02, df = 2, lower.tail = FALSE)

## [1] 0.22091

Summary of Example

When we have a multinomial experiment, we can use EMT::multinomial.test to obtain exact \(p\)-values associated with the null hypothesis \(H_0: p_1 = p_{10}, \cdots, p_k = p_{k0}\) versus \(H_a\), which is that not all of the probabilities are as specified. Use multinomial.test(observed, prob, MonteCarlo = TRUE) if the multinomial experiment is large. Alternatively, use the \(\chi^2\) approximation given by chisq.test. For strict multinomial problems, I prefer EMT::mutlinomial.test.

9.3 \(\chi^2\)-tests

As mentioned above, the \(\chi^2\) approximation of Pearson’s statistic is useful in more contexts than a pure multinomial setting. For example, goals per soccer game is often thought of as being approximately Poisson. How would one perform a hypothesis test to determine whether that a Poisson model is a good fit?

I collected the number of goals scored in each of the 2015 FIFA World Cup games, and have stored them in the variable goals below.

goals <- c(1,0,0,1,1,0,0,0,1,1,2,2,4,0,10,0,1,1,2,3,0,4,1,3,6,0,1,0,10,1,2,1,0,1,1,2,3,3,3,1,2,0,0,0,0,1,1,1,1,1,2,0,1,0,2,2,0,1,2,1,1,0,1,1,0,2,2,1,0,5,2,1,4,1,1,0,0,1,3,0,1,0,1,2,2,0,2,1,1,1,0,1,0,1,2,1,2,0,2,1,0,1,5,2)

One thought would be to determine what the deviation from expected is, and then determine the probability of observing a deviation that far from expected. If we use Pearson’s \(\chi^2\) statistic, an issue comes up that the expected value of the bin is in the downstairs, so if we have a bin with one observation that had a low expected value, then that could really mess things up. For this reason, it is traditional to ensure that the expected value of each bin is at least 5.

Another issue is that we don’t know what the true mean of the underlying Poisson random variable should be, so we will need to estimate it from the data. When we do so, the values in the bins fit the expected values better than they should, so we will need to make an adjustment. (See simulations below.)

So, the process is, estimate the mean of the Poisson random variable by averaging the values observed.

lambda <- mean(goals)

In this case, we get \(\lambda = 1.40\), or so. Then, since we have 104 observations, we want the probability of each bin to be at least 5% (so that the expected number of occurrences in each bin is at least 5).

dpois(0:5, lambda)

## [1] 0.24565034 0.34485528 0.24206188 0.11327255 0.03975431 0.01116179

We can see that we will need to bin the observations into zero goals, one goal, two goals, three goals, or 4+ goals. The expected outcomes are

expected_goals <- 104 * c(dpois(0:3, lambda), ppois(3, lambda, lower.tail = FALSE))
round(expected_goals, 1)

## [1] 25.5 35.9 25.2 11.8  5.6

Now, we need to get the observed goals:

table(goals)

## goals
##  0  1  2  3  4  5  6 10 
## 30 40 20  6  3  2  1  2

observed_goals <- c(30, 40, 20, 6, 7)

The Pearson’s \(\chi^2\) statistic is

sum((observed_goals - expected_goals)^2/expected_goals)

## [1] 5.484486

The key fact is that this test statistic is approximately \(\chi^2\) with degrees of freedom equal to the number of bins minus one minus the number of parameters that were estimated from the data. In this case, we have 5 bins and one parameter estimated, so it is \(\chi^2\) with 3 degrees of freedom. The \(p\)-value is the probability of getting a test statistic of 5.484486 or bigger, under the null hypothesis, which is

pchisq(5.484486, df = 3, lower.tail = FALSE)

## [1] 0.1395695

So, the \(p\)-value of this test is 0.1396, and we would not reject \(H_0\) at the \(\alpha = .05\) level. Note that there may be other aspects of this data set (such as the unlikely event that 10 goals were scored on two different occassions) that are highly unlikely under the assumption that the data comes from a Poisson random variable, but this test does not consider that. In particular, if you believe that your data might not be Poisson because you suspect it will have unusually large tails (rather than unusually many), then this test will not be very powerful.

9.3.1 Simultations

Now, we investigate why we need to take the number of bins minus one minus the number of parameters estimated. Let’s suppose that the underlying process really is Poisson with mean 2, and we collect 200 data points.

my_data <- rpois(200, 2)
table(my_data)

## my_data
##  0  1  2  3  4  5 
## 27 59 45 45 17  7

In order to do a fair simulation, I need to select both the number of bins and the probabilities of the bins based on the data, because that is the procedure that I outlined above. However, my choice of 200 and 2 lead to almost always having 6 bins, so we ignore that technicality.

lambda <- mean(my_data)

N <- 4
observed <- table(my_data)[1:(N + 1)]
observed <- c(observed, 200 - sum(observed))
expected <- c(dpois(0:N, lambda), ppois(N, lambda, lower.tail = FALSE)) * 200
test_stat <- sum((observed - expected)^2/expected)

test_stat

## [1] 5.367836

Now, we replicate. We throw away any data that doesn’t lead to the most likely outcome of 6 bins.

sim_data <- replicate(10000, {
  my_data <- rpois(200, 2)
  lambda <- mean(my_data)
  if(lambda >= 1.62 && lambda < 2.20) { #Six bins
    N <- 4
    observed <- table(my_data)[1:(N + 1)]
    observed <- c(observed, 200 - sum(observed))
    expected <- c(dpois(0:N, lambda), ppois(N, lambda, lower.tail = FALSE)) * 200
    test_stat <- sum((observed - expected)^2/expected)
  } else{
    test_stat <- NA
  }
  test_stat
})
hist(sim_data, probability = TRUE, ylim = c(0, .19))
curve(dchisq(x, 4), add = TRUE, col = 2)
curve(dchisq(x, 5), add = TRUE, col = 3)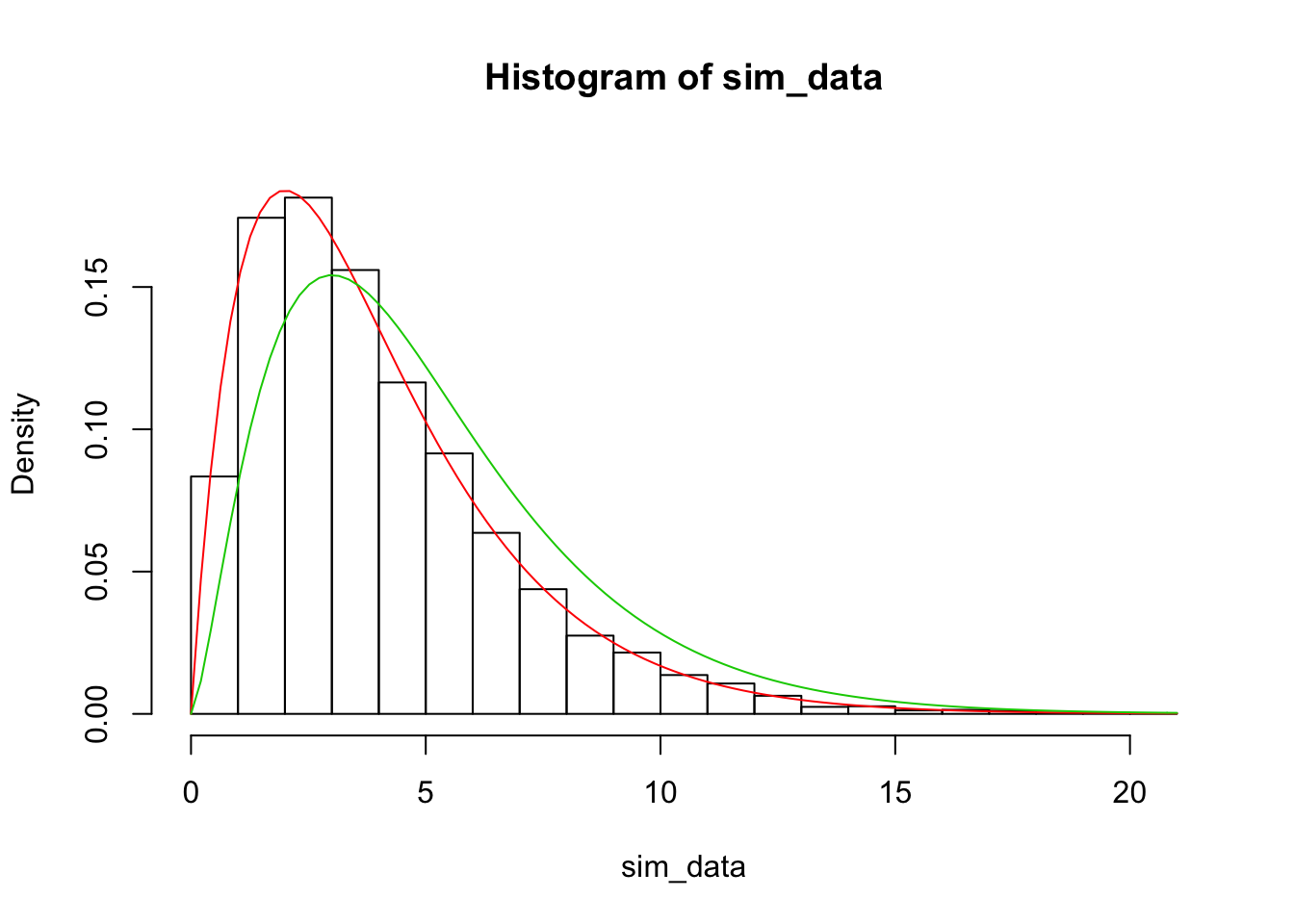

Note that the red curve above is associated with the correct degrees of freedom (bins - parameters - 1) = 4, while the green curve would have been just (bins - 1), which is clearly incorrect. This seems to be pretty compelling.

9.4 Exercises

A paper by Diaconis, Holmes and Montgomery suggests that there is a dynamical bias in coin tossing that leads ofr coins to more often land on the same side they were released from than the other way. In a real coin-tossing experiment described here, two students tossed coins a total of 40 thousand times in order to assess whether this is true. Out of the 40K tosses, 20,245 landed on the same side as they were tossed from.
1. Find a (two-sided) 99% confidence interval for \(p\), the true proportion of times a coin will land on the same side it is tossed from.
2. Clearly state the null and alternative hypotheses, defining any parameters that you use.
3. Is there sufficient evidence to reject the null hypothesis at the \(\alpha = .05\) level based on this experiment? What is the \(p\)-value?
(Hard) Suppose you wish to test whether a die truly comes up “6” 1/6 of the time. You decide to roll the die until you observe 100 sixes. You do this, and it takes 560 rolls to observe 100 sixes.
1. State the appropriate null and alternative hypotheses.
2. Explain why prop.test and binom.test are not formally valid to do a hypothesis test.
3. Use reasoning similar to that in the explanation of binom.test above and the function dnbinom to compute a \(p\)-value.
4. Should you accept or reject the null hypothesis?
Consider the UsingR::normtemp dataset. Use a goodness of fit test with 10 bins, all with equal probabilities, to test the normality of the temperature data set. Note that in this case, you will need to estimate two parameters, so the degrees of freedom will need to be adjusted appropriately.