Chapter 6 Data Visualization with ggplot

In this chapter, we show how to use ggplot to create scatterplots, boxplots and histograms. (Note that using geom_line() was discussed in Chapter 5).

6.1 Scatterplots

Following Wickham’s example in Chapter 2 of his book, let’s consider the mpg data set in the library ggplot2. (Why 211?)

The function ggplot takes as its first argument the data frame that we are working with, and as its second argument the aesthetics mappings between variables and visual properties. In this case, we are telling ggplot that the aesthetic “x-coordinate” is to be associated with the variable displ, and the aesthetic “y-coordinate” is to be associated to the variable hwy. Let’s see what that command does all by itself:

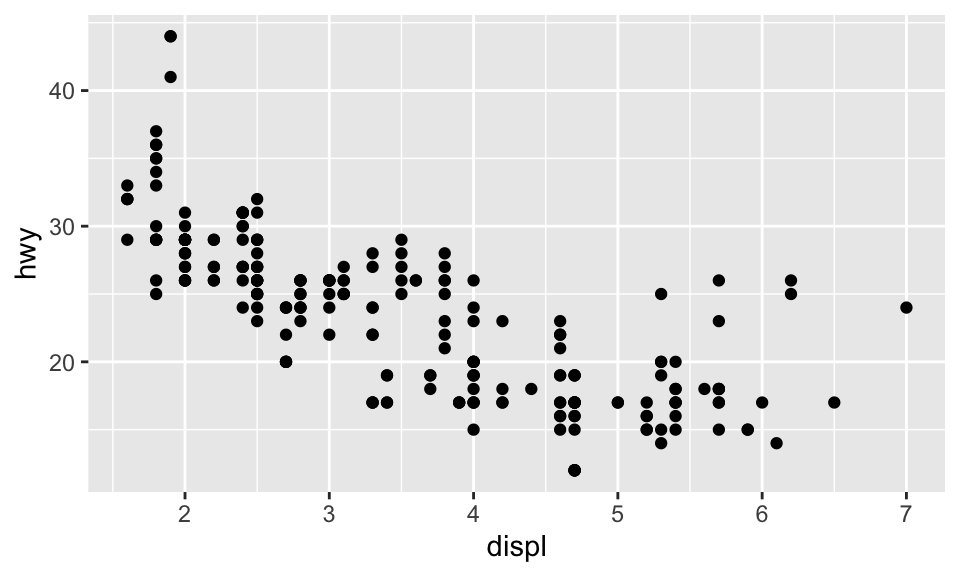
ggplot has set up the x-coordinates and y-coordinates for displ and hwy. Now, we just need to tell it what we want to do with those coordinates. That’s where geom_point comes in. The function geom_ point() inherits the x and y coordinates from ggplot, and plots them as points. geom_line() would plot a line.

## `geom_smooth()` using method = 'loess' and formula 'y ~ x'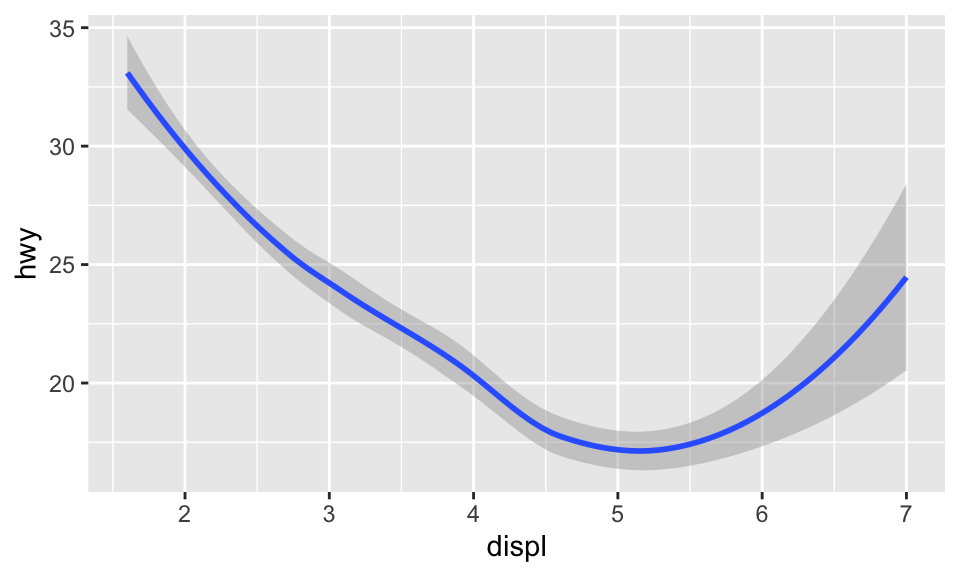

There are tons of other geoms that you can use! For example, how would you create a boxplot of hwy versus drv?

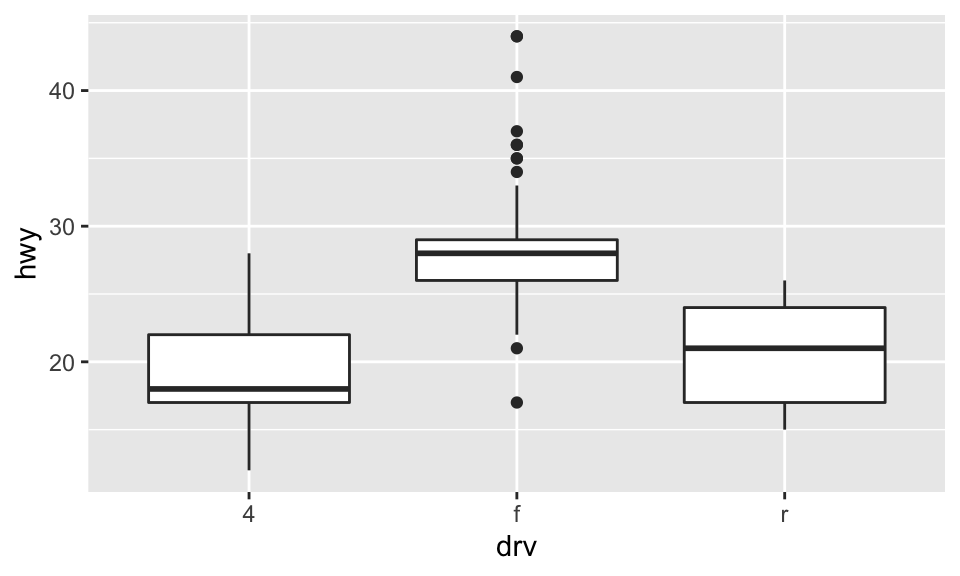
Exercises

  1. Plot igf1 versus age in the ISwR::juul data set.
  2. Plot igf1 versus age in the ISwR::juul data set, but color code the points according to tanner puberty level!

You can definitely do the first one. Do that before looking at how to do the second one below.

Solution to exercise 2.

## Warning: Removed 326 rows containing missing values (geom_point).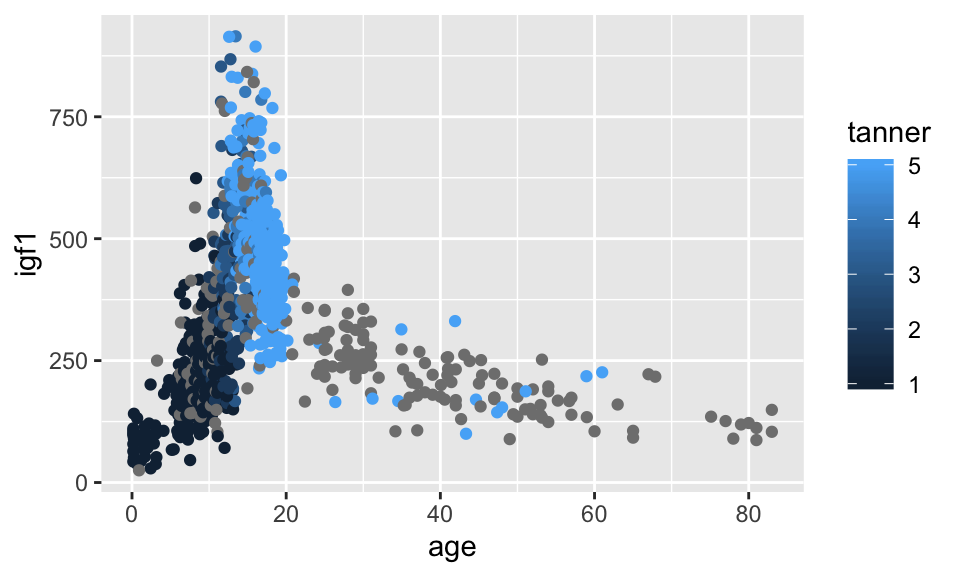

This solution leaves something to be desired, because the points with no tanner level assigned are given values of gray, which makes it a little hard to see what is going on. Let’s redo with the tanner values of NA removed.

## Warning: Removed 307 rows containing missing values (geom_point).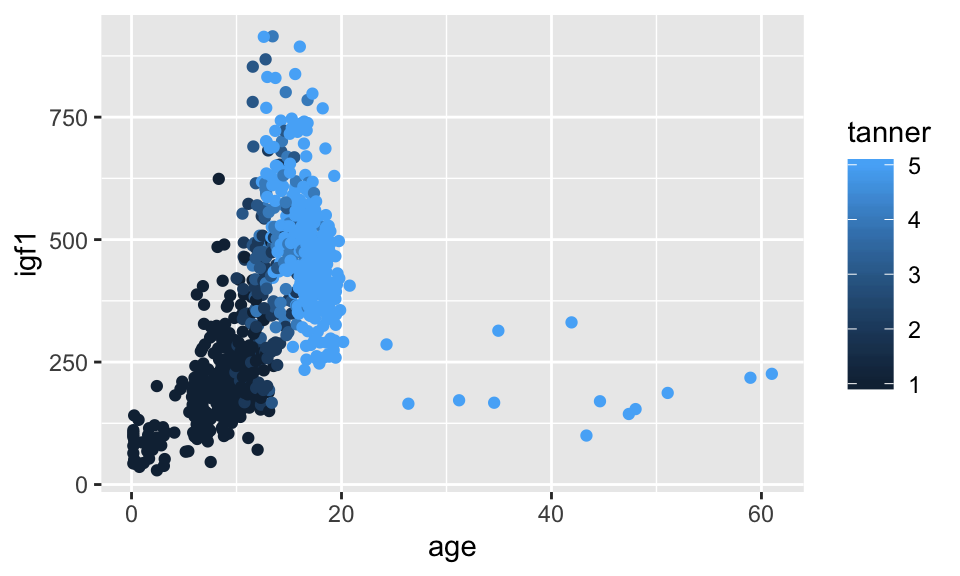

If we only wanted tanner I-IV, we could do

## Warning: Removed 287 rows containing missing values (geom_point).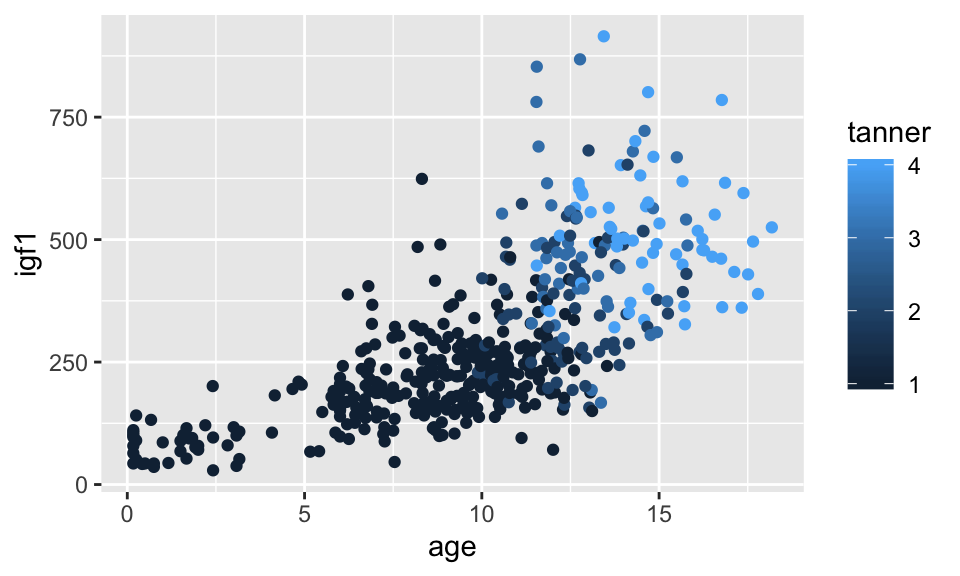

Remember that juul encodes tanner as numeric, when it is probably better thought of as a factor. Let’s switch it to a factor and see what happens to the graph:

## Warning: Removed 307 rows containing missing values (geom_point).

I might not say that this is the definitive graph of this data set, but it is definitely much better than anything we did before learning about ggplot. Note that the default colors change when the color aesthetic is a factor. This makes sense, because when it is a factor you want to be able to distinguish between the factors. If it is an integer or real number, you want to be able to see the continuum of change.

6.2 Boxplots

We aren’t going to say a lot about boxplots. Let’s create a boxplot of igf1 level.

## Warning: Removed 321 rows containing non-finite values (stat_boxplot).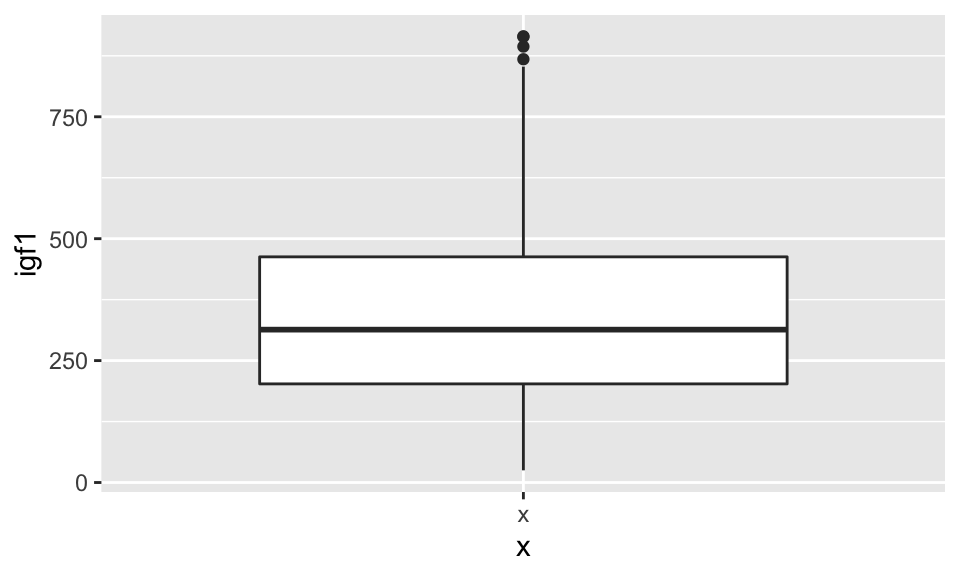

The thick line in the middle is the median of the data, and the top and bottom lines of the rectangle are the 75th and 25th percentile, respecitvely. The whiskers extend from the rectangle out to either 1.5 times the difference between the 75th and 25th percentiles, or out to the last point in the data, whichever is nearest. Points that fall outside of the whiskers are plotted individually.

If we want to create multiple boxplots, say one for each gender, we would use

## Warning: Removed 321 rows containing non-finite values (stat_boxplot).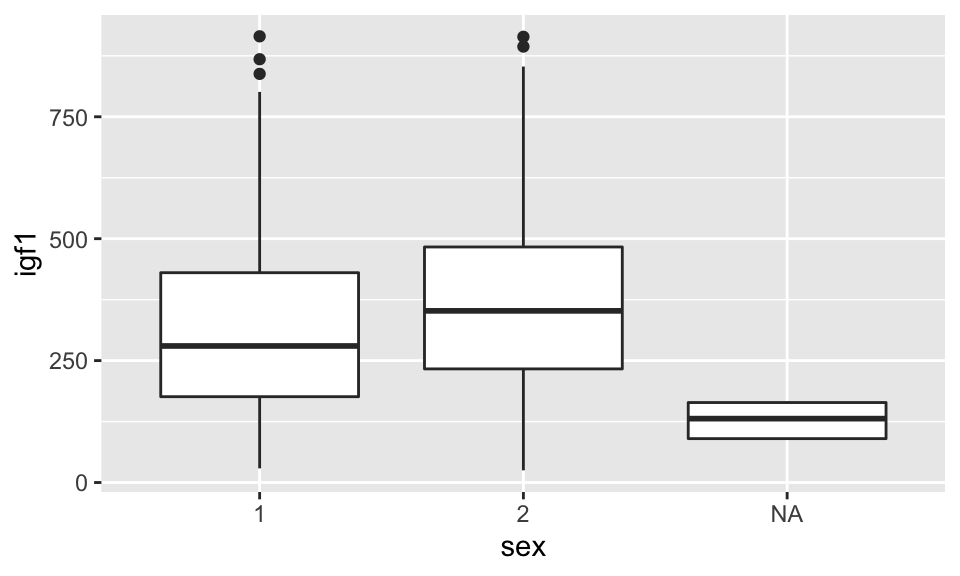

It is useful that the NA shows up here. We see that there seems to be a correlation between whether sex was reported and igf1 levels. We would definitely want to keep that in mind as we progress with analysis. Looking at this, it is natural to wonder whether there is a difference in the igf1 levels between males and females. It is very challenging to look at a standard boxplot and have much of an idea whether there is a difference! For that, we would want to use a notched boxplot, which provides a visual representation of an error estimate for the median.

## Warning: Removed 321 rows containing non-finite values (stat_boxplot).
## notch went outside hinges. Try setting notch=FALSE.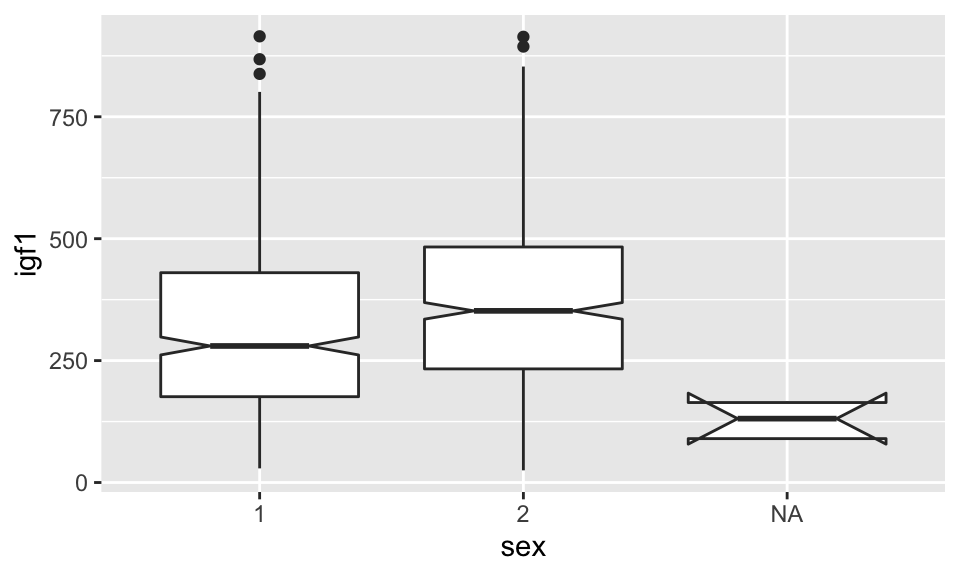

The notches in the boxplots correspond to an error estimate for the median. (We will learn more about this for error estimates of the mean in Chapter 7.) Since the error estimates are disjoint, that is evidence that perhaps boys and girls have different igf1 levels.

Let’s do the same for tanner level.

## Warning: Removed 321 rows containing non-finite values (stat_boxplot).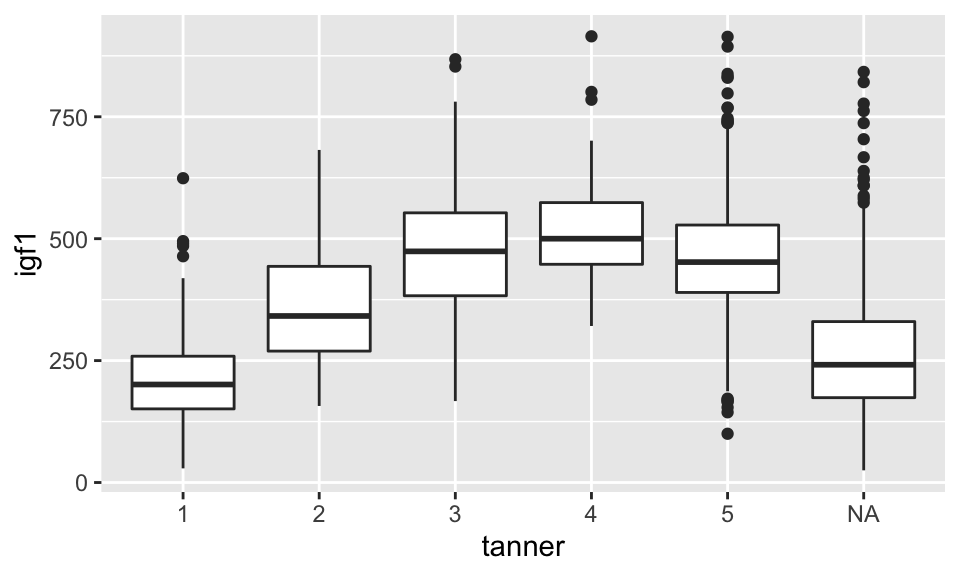

6.3 Histograms

Let’s look at the juul igf1 data again. If we just want a histogram of the igf1 data, we use:

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## Warning: Removed 321 rows containing non-finite values (stat_bin).

Unlike the base R function hist, geom_boxplot does not try to guess an appropriate number of bins for the histogram. Instead, it always defaults to 30 and recommends that you pick a better value. Let’s examine the histogram with a couple of different number of bins. When using geom_histogram, you will usually need to play with the number of bins until you find a value that you feel faithfully represents the data.

## Warning: Removed 321 rows containing non-finite values (stat_bin).

## Warning: Removed 321 rows containing non-finite values (stat_bin).

It’s a little bit hard to tell what is going on. Since we have done the scatterplot already, we know that the igf1 levels are very different for the various tanner puberty levels. So, let’s plot igf1 level by tanner puberty level.

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## Warning: Removed 321 rows containing non-finite values (stat_bin).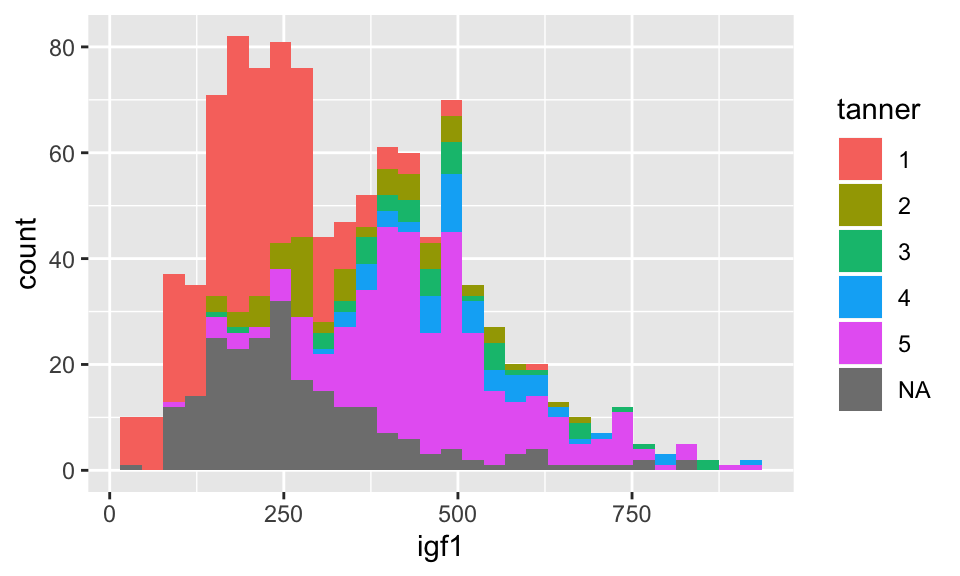

It is hard to see what is going on here. Better would be if we had each histogram plotted on its own axes. In the graphical lexicon, that is called faceting. We will use the ggplot2 function facet_wrap to do this:

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## Warning: Removed 321 rows containing non-finite values (stat_bin).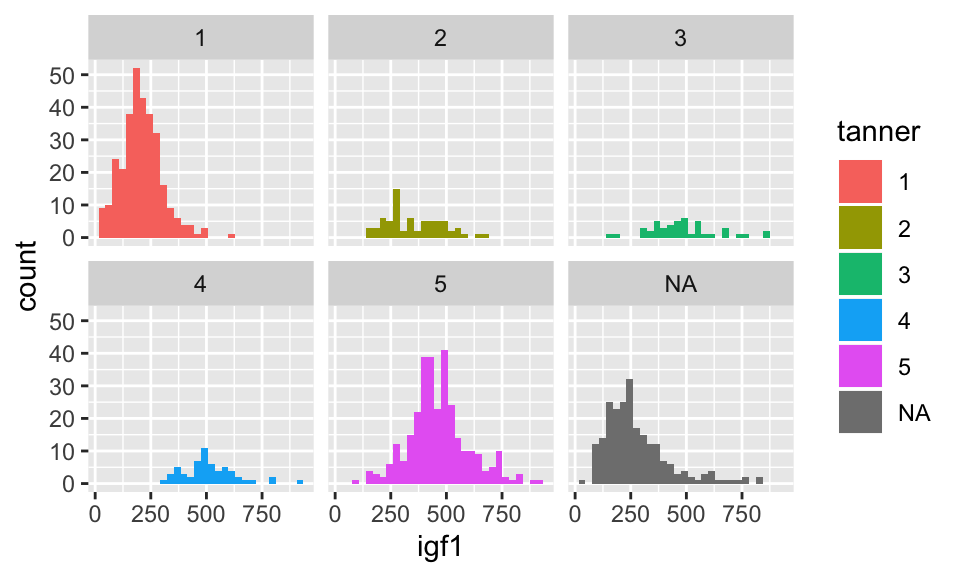

Now, though, the colors don’t mean anything, so we could color by another variable instead of tanner, such as by sex.

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## Warning: Removed 321 rows containing non-finite values (stat_bin).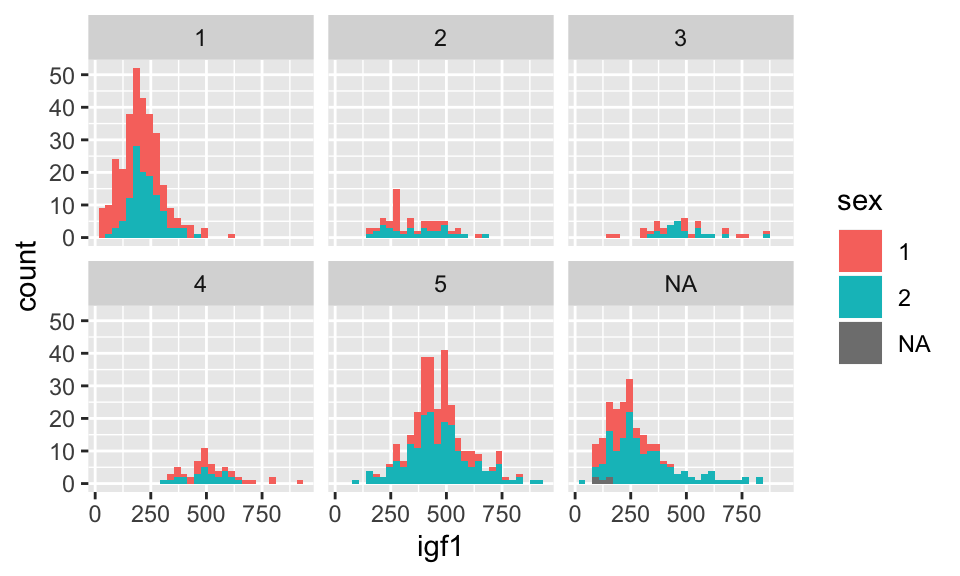

Normally when faceting plots like this, we want the axes the same for all the plots, as is the case above. Occasionally, we prefer to free up the axes so that they are not all on the same scale. We can do that as follows:

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
## Warning: Removed 321 rows containing non-finite values (stat_bin).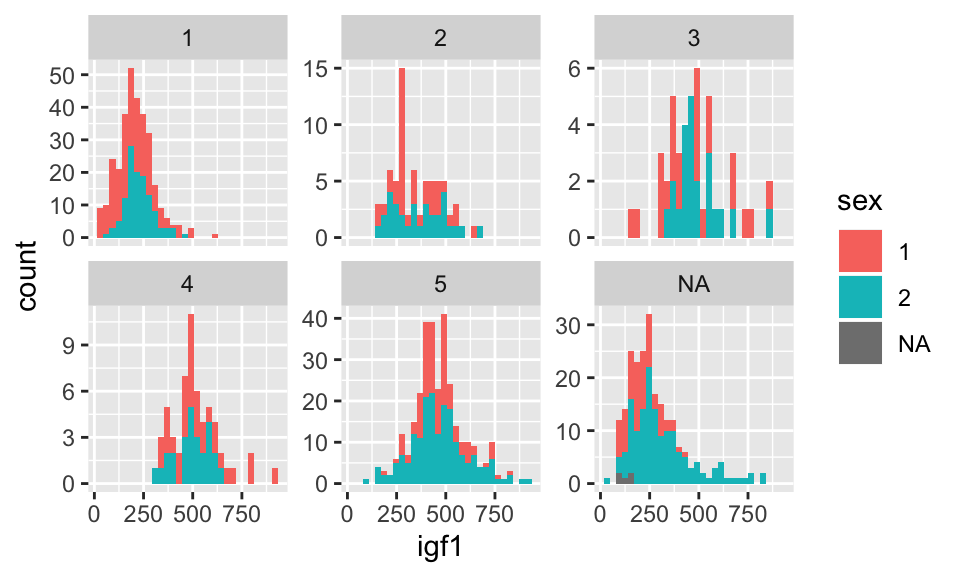

There is still quite a bit of work to do to finalize this plot. It would be nice to have different bin sizes for the different facets, and we need to relabel sex as boy and girl, instead of 1 and 2. We also could change the top label of each plot to indicate that it is tanner level 1, tanner 2, and so on. The interested reader can find information on how to do this in Wickham’s book, ggplot2.

6.4 Quantile-Quantile plots

In Chapter ??, we saw how to estimate a density function from data and compare it to a known density function in order to decide whether data (plausibly) comes from a specified distribution. Another way to compare a sample with a known distribution is by using qq plots. Unlike density estimation, qq plots do not have any extra parameters that need to be selected, and qq plots can be easier to interpret.

What is a qq plot? Well, suppose you have a random sample of size \(N\) from an unknown distribution, and you want to create a qq plot to compare this to a uniform distribution on the interval \([0,1]\). You would order the data points from smallest to largest, which we denote by \(X_{(1)}, \ldots, X_{(N)}\). Then, you would compare the ordered data points to the expected value of the ordered data points, which in this case turns out to be \(1/(N+1), \ldots, N/(N+1)\) (trust me on this, or look ahead to Section @ref(order_statistics)). One way to compare would be to plot the ordered pairs \[ (X_{(1)}, \frac 1{N+1}), \ldots, (X_{(n)}, \frac {N}{N+1}) \] Such a plot is called a qq plot. If the sample comes from a uniform \([0,1]\) random variable, then we would expect the ordered pairs to roughly fall on a straight line. Otherwise, we would not expect the ordered pairs to fall on a straight line with slope 1. The algorithm that R uses is a bit more complicated than the above, but it is mostly only noticeable when the data set is small.

Let’s look at an example. Here, we take a random sample from a normal distribution with mean 0 and standard deviation 1, and create a qq plot to compare it to a normal(0, 1) random variable. The result should be approximately a straight line.

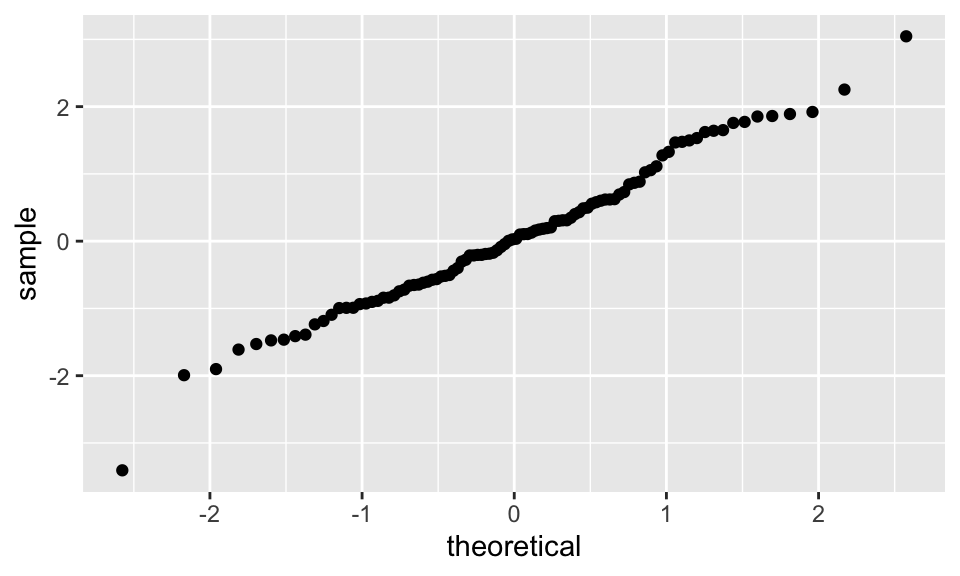
Note that the data very approximately follows a straight line with slope 1. Now, let’s see what happens when our data comes from a heavy-tailed distribution such as t:

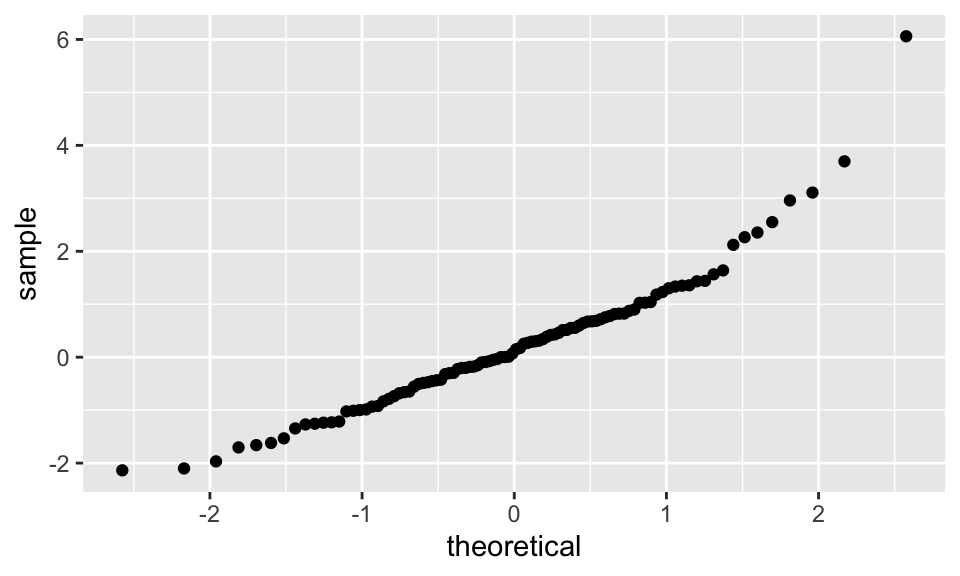
Note that the qq plot now has an S shape. Light tailed distributions also have an S shape when compared to normal, but the S goes the other way.

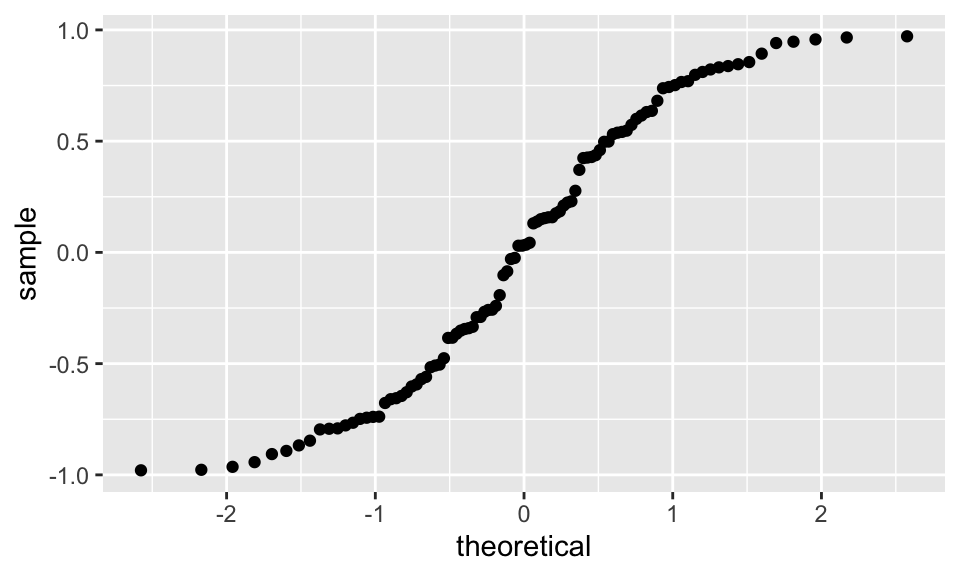Finally, skewed data tends to have a U shape when compared to normal:

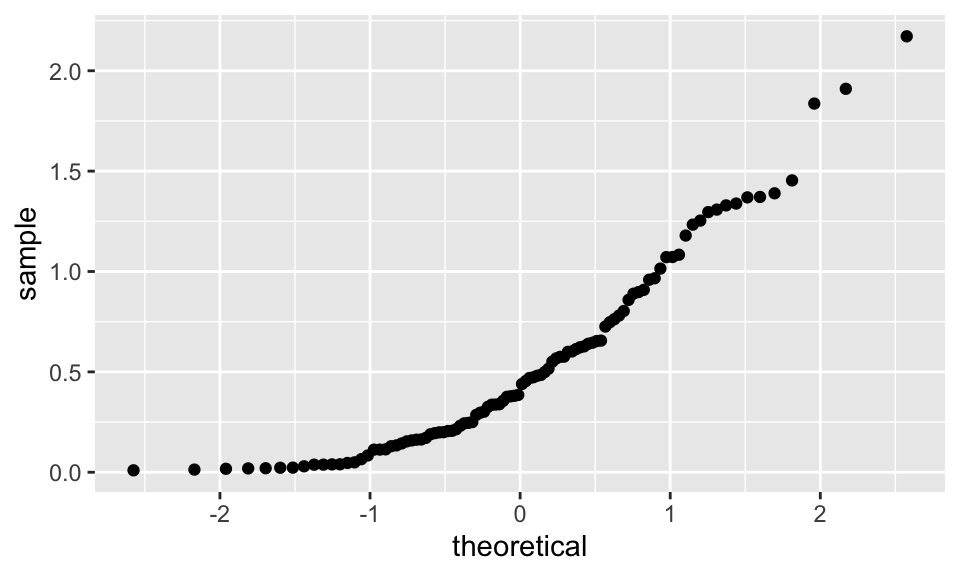
It is possible to compare our data to other distributions, as well as to compare two samples, but we will leave that for another class.

6.4.1 qq plots by hand

Suppose we have 5 points, and we wish to make a qq plot versus a standard normal random variable. The key step is finding the expected value of the minimum, second largest, and so on. To do this, we will make a matrix that has 5 columns and 10,000 rows worth of random observations of a normal rv. We will sort each row, and then take the mean of each column. The values we obtain are estimates for the expected value of the order statistics.

Now, let’s get some data:

## [1] -1.2070657  0.2774292  1.0844412 -2.3456977  0.4291247

sort it and put it inside a data frame, then plot it:

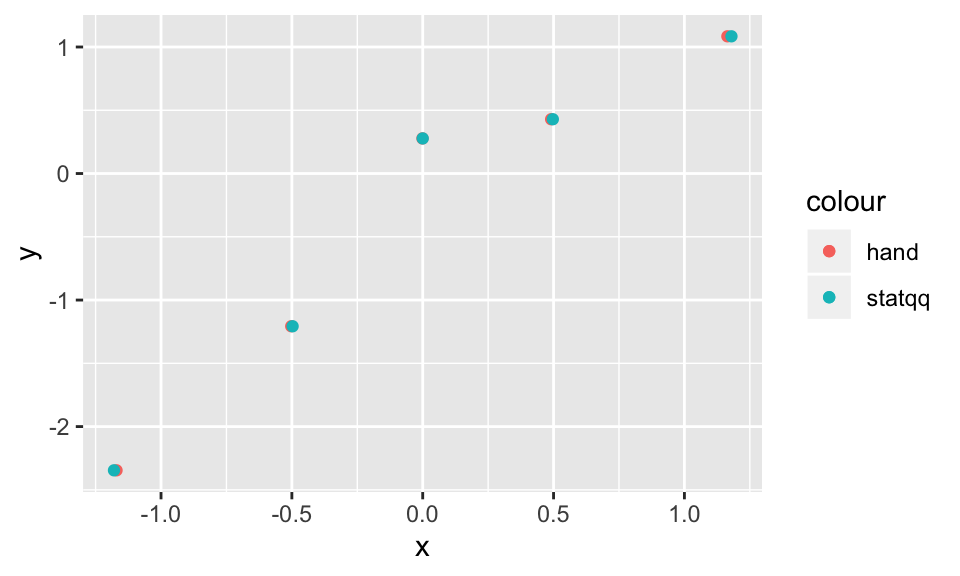
As you can see, our results by hand are very close to the results that stat_qq gives, but not exact. The reason for this is twofold: first, we have estimated the expected values of the order statistics, which will introduce some error. Second, stat_qq uses a modified version of the above algorithm that tends to give very similar, but slightly different results. For details, see the documentation of qqplot in base R, which stat_qq is modeled off of.

6.5 Plotting pmfs

In this section, we illustrate the use of dplyr tools and geom_bar to plot pmf’s. This was introduced in 4.2. There are two possibilities. In the first, you wish to store the tabulated data in a data frame and plot it. The verb count is the dplyr tool that most closely mimics the base function table. We illustrate its usage here:

## # A tibble: 6 x 2
##       x     n
##   <int> <int>
## 1    11     3
## 2    12     4
## 3    13     1
## 4    14     7
## 5    15     9
## 6    16    12

Note that we really would prefer the proportion of values rather than the raw count in poisTable. So, we need to mutate the data frame:

## # A tibble: 6 x 3
##       x     n  prop
##   <int> <int> <dbl>
## 1    11     3 0.015
## 2    12     4 0.02 
## 3    13     1 0.005
## 4    14     7 0.035
## 5    15     9 0.045
## 6    16    12 0.06

Now, it is a simple matter to call ggplot, using the geom geom_bar:

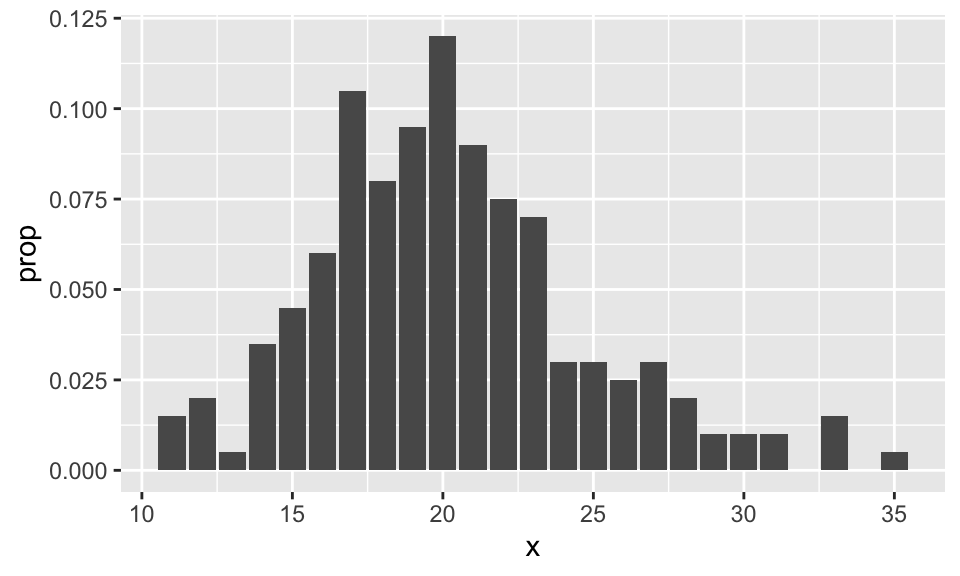
The second way is easier, but requires usage of the mystical ..count.. argument. It assumes that you have the un-tabulated data. In this case, you simply use geom_bar with only one aesthetic.

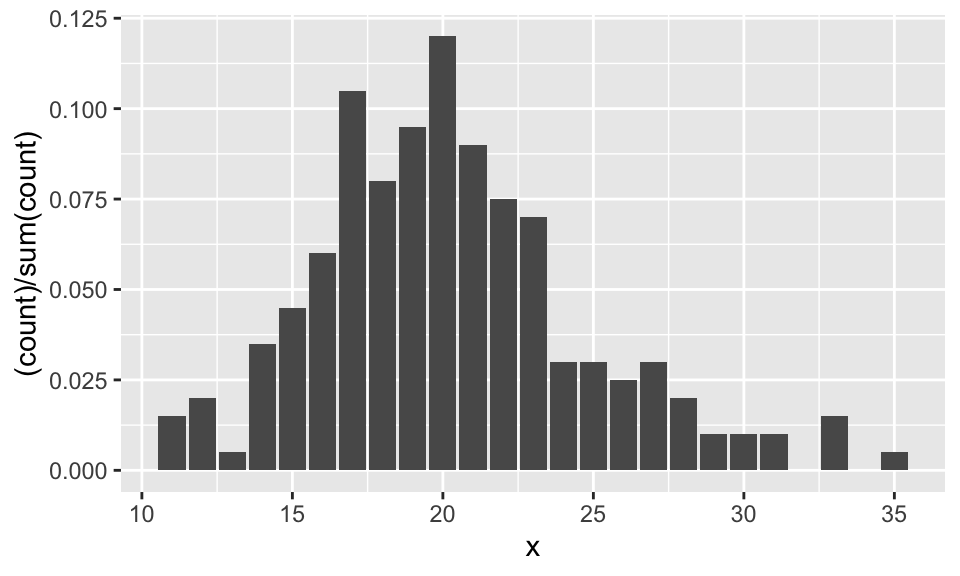
Let’s clean up that \(y\)-axis label:

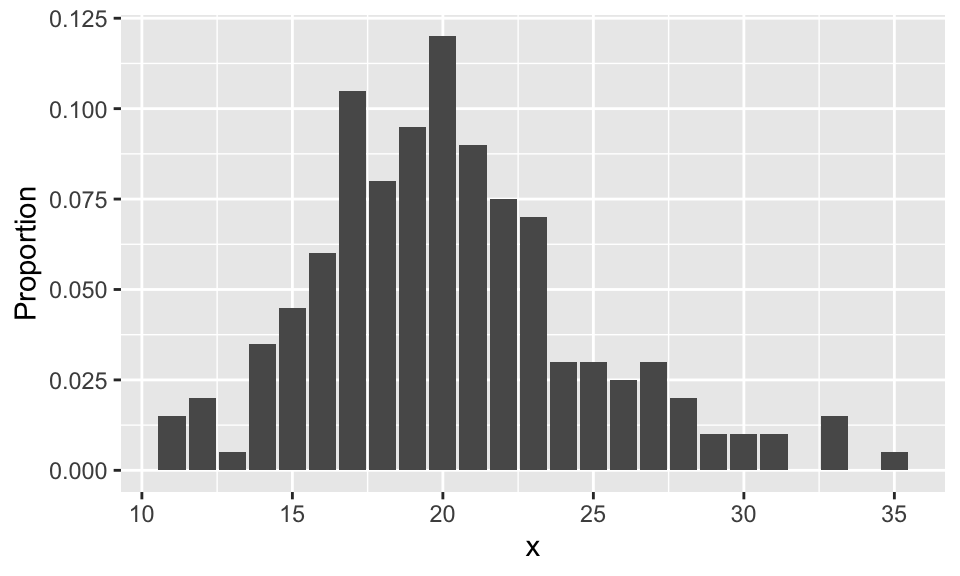
6.6 Plotting functions

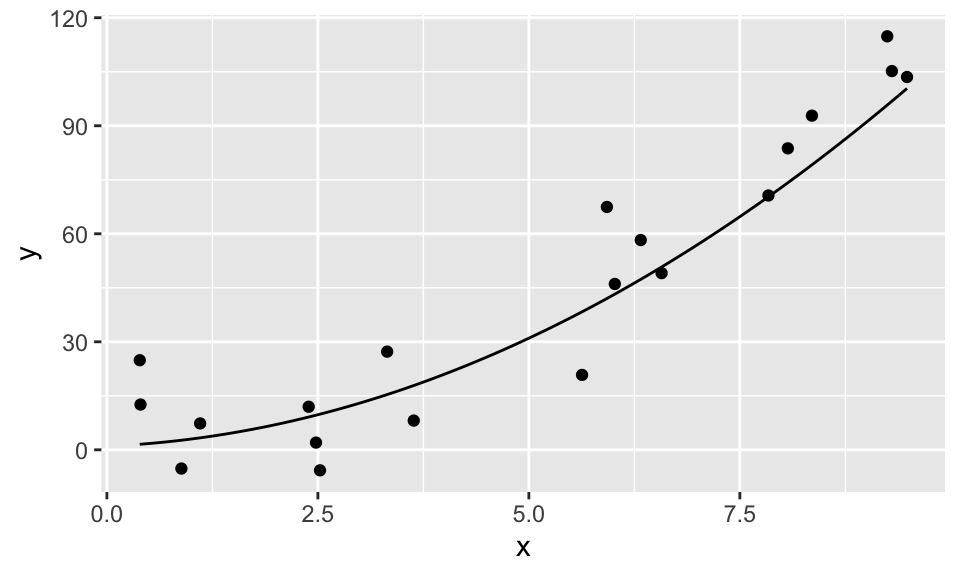
Sometimes, you would like to plot the graph of a function, like \(y = x^2\). While ggplot2 might not be the most convenient tool for doing that, it is easy to do that if you want to plot functions on top of a scatterplot. Let’s look at an example.

Suppose you are given data that more or less lies along the curve \(y = x^2 + x + 1\), and you wish to plot the data and the curve \(y = x^2 + x + 1\) on the same plot. The easiest way to do so is with the stat_function function.

Let’s plot the data:

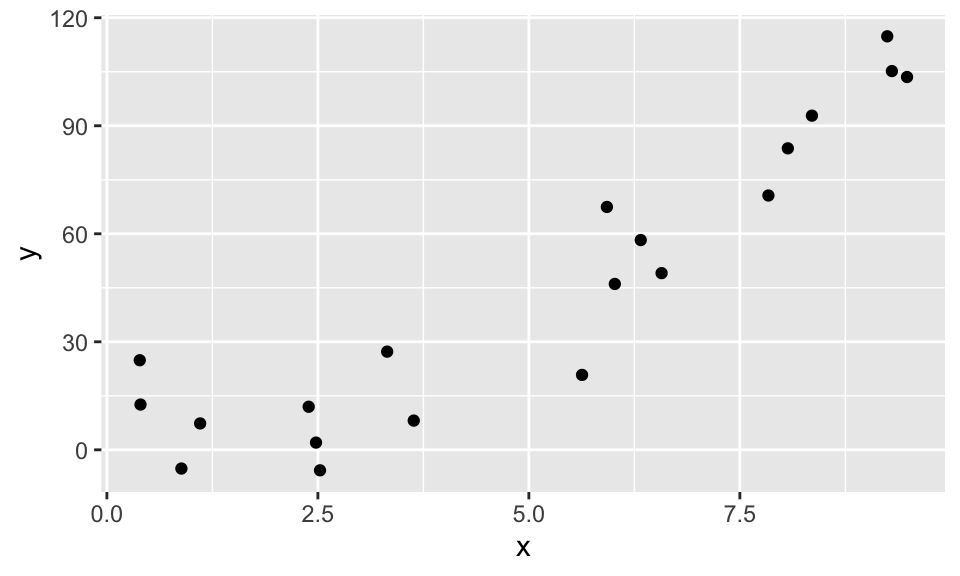
And here is how you use stat_function. Note that stat_function is really nice for plotting functions, but it can sometimes be challenging to get correct colors and labeling. An alternate approach is to define a new dataframe containing \(x\) and \(y\) coordinates for the function you wish to plat, then use geom_line to draw the curve.

6.7 Piping to ggplot

Combining the ideas from last chapter with the above, we can easily create plots after manipulating a large data set to contain the information that we want to see. Let’s consider the movieLens data set from Chapter @ref(data_manipulation), and make sure that you have dplyr loaded.

Let’s create a barplot of ratings for movies with the genre Comedy|Romance.

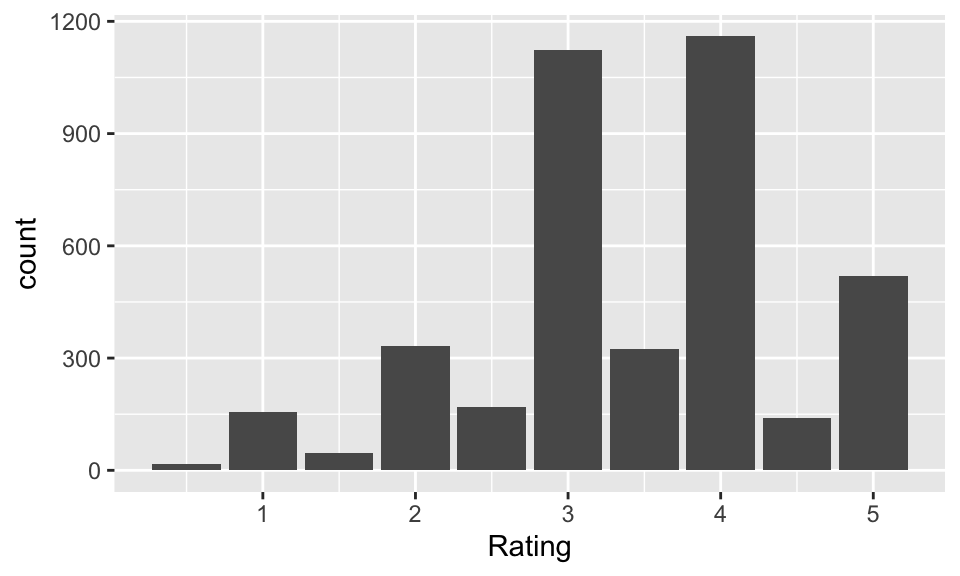
6.8 Common ggplot issues

Data for ggplot must be stored as a data frame (or equivalent structure, such as a tibble). In particular, ggplot cannot work with a vector by itself.

Example Consider the rivers data set in base R. Create a histogram of the lengths of the rivers.

To do this, we first see what type of data set rivers is:

##  num [1:141] 735 320 325 392 524 ...

And, we see that it is a numerical vector. We must convert it to a data frame to use ggplot.

##   length
## 1    735
## 2    320
## 3    325
## 4    392
## 5    524
## 6    450

Now, we can use ggplot:

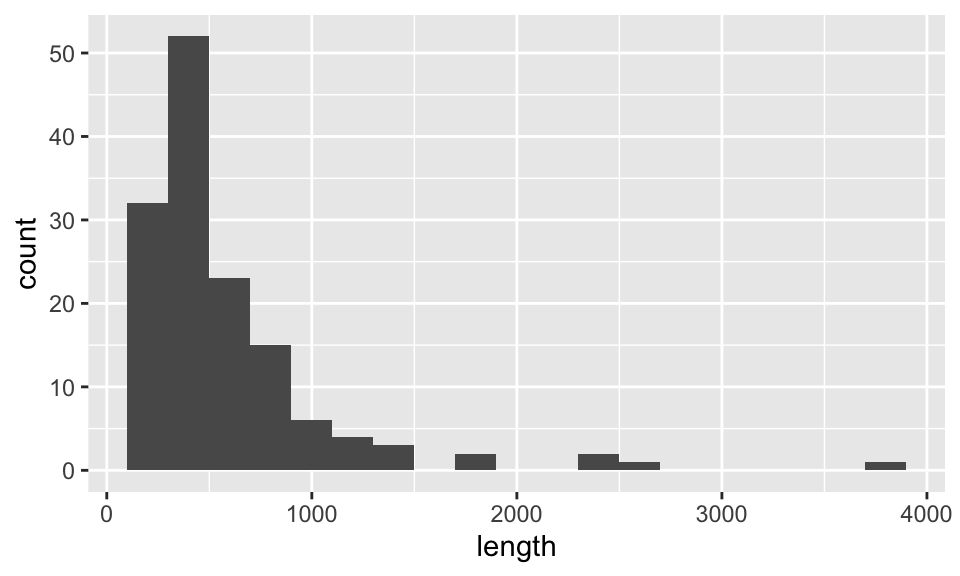
The next example illustrates two other common issues with ggplot. Although to be fair, both of these issues are issues with the underlying data representation, and not with the plotting tool. When the data is finally tidy, the plot becomes simple.

Example 6.1 Consider the anorexia data in the MASS library. Create a side-by-side boxplot of the Pre- and Post-treatment weights of the patients in the CBT group.

Let’s look at the data.

##   Treat Prewt Postwt
## 1  Cont  80.7   80.2
## 2  Cont  89.4   80.1
## 3  Cont  91.8   86.4
## 4  Cont  74.0   86.3
## 5  Cont  78.1   76.1
## 6  Cont  88.3   78.1

Note the use of MASS::anorexia to pull out the data set from the library, since we don’t want the entire MASS library loaded into our R session.

The plot we want needs to be able to specify Pre- and Post- values as an aesthetic, and aesthetics are assigned to variables. However, the Pre/Post information is not stored in a variable. Instead, is stored in the column names. There should be a variable called Phase that describes which phase of the experiment when the weight was measured. We can pivot the information from the column names into the desired Phase variable using pivot_longer:

## # A tibble: 6 x 3
##   Treat Phase  Weight
##   <fct> <chr>   <dbl>
## 1 Cont  Prewt    80.7
## 2 Cont  Postwt   80.2
## 3 Cont  Prewt    89.4
## 4 Cont  Postwt   80.1
## 5 Cont  Prewt    91.8
## 6 Cont  Postwt   86.4

Now, the values Prewt and Postwt are values of a variable, and can be assigned to the x aesthetic. We send the data to ggplot after filtering just the CBT treatments.

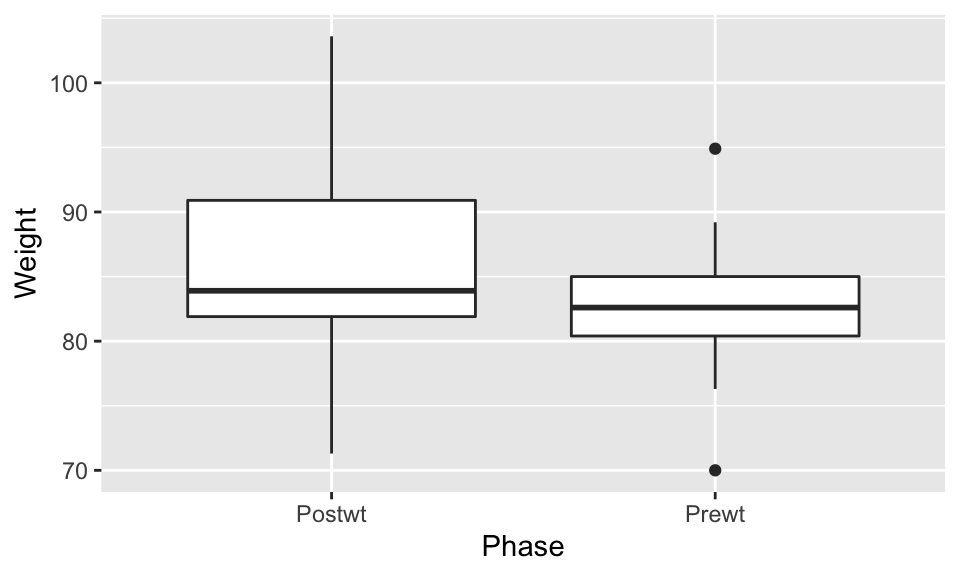
Observe that the phases of the experiment are backwards (read left to right). The Prewt measurement actually came first, followed by the Postwt measurement. The plot put the two values Postwt/Prewt in alphabetical order. The issue is with the underlying nature of the data, not with the plot itself, and the fix is to correctly specify the order as a feature of the data itself.

The Phase variable is currently a character type, when it should be an ordered factor. The factor function in base R can convert Phase to a factor, and along the way set the order of the levels:

The Phase variable now has the correct structure

##  Factor w/ 2 levels "Prewt","Postwt": 1 2 1 2 1 2 1 2 1 2 ...

and so the plot shows the phases in the correct order:

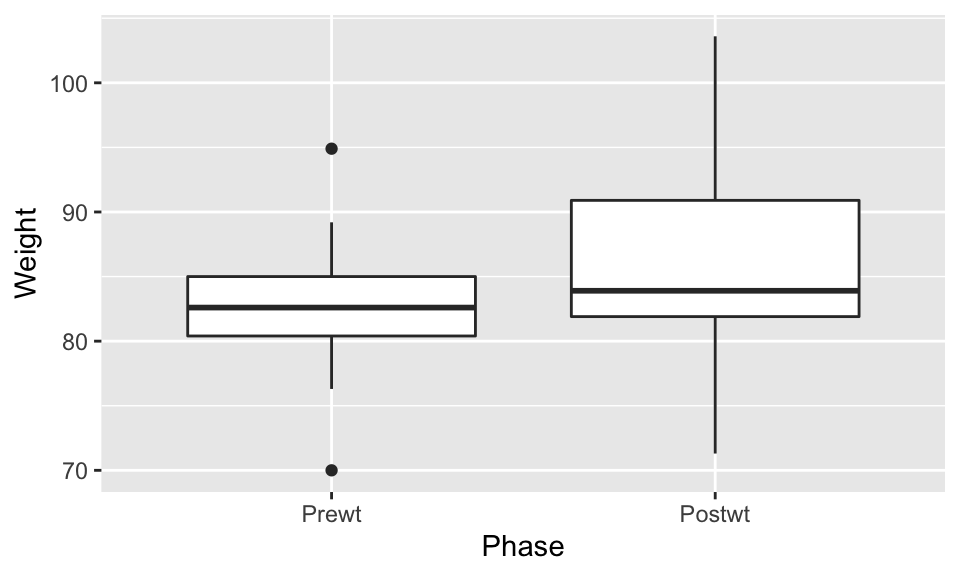
Perhaps the subjects of this experiment gained weight when treated with CBT.

6.9 Example: Votes in Alabama

Consider the data set that was created in Section @, which can be loaded by typing

This data set contains the number of votes for each candidate in the 2012 presidential election, the population, and the unemployment rate of each county in Alabama. Let’s first look at summary data:

##  State.Postal       County.Name             FIPS        Obama.vote    
##  Length:68          Length:68          Min.   :   0   Min.   :   971  
##  Class :character   Class :character   1st Qu.:1032   1st Qu.:  3336  
##  Mode  :character   Mode  :character   Median :1066   Median :  5448  
##                                        Mean   :1051   Mean   : 23342  
##                                        3rd Qu.:1100   3rd Qu.:  9980  
##                                        Max.   :1133   Max.   :793620  
##                                                                       
##        X.         Romney.vote           X..1            pop        
##  Min.   :12.30   Min.   :    799   Min.   :12.70   Min.   :  3250  
##  1st Qu.:24.35   1st Qu.:   5420   1st Qu.:53.02   1st Qu.:  7358  
##  Median :33.90   Median :   9014   Median :65.15   Median : 15346  
##  Mean   :38.44   Mean   :  36837   Mean   :60.78   Mean   : 31119  
##  3rd Qu.:46.50   3rd Qu.:  25394   3rd Qu.:74.62   3rd Qu.: 35110  
##  Max.   :87.10   Max.   :1252453   Max.   :86.50   Max.   :299680  
##                                                    NA's   :1       
##      unemp      
##  Min.   : 7.50  
##  1st Qu.: 9.90  
##  Median :11.90  
##  Mean   :12.69  
##  3rd Qu.:14.75  
##  Max.   :25.60  
##  NA's   :1

I changed the variable names associated with the percentage votes to something meaningful. Next, notice that the median value of Obama.vote, Romney.vote and pop are all much less than their means. This is an indicator of skewness, and we may want to consider plotting those variables on a log-scale.

Let’s start by creating a scatterplot of the percentage of Obama votes versus unemployment.

## Warning: Removed 1 rows containing missing values (geom_point).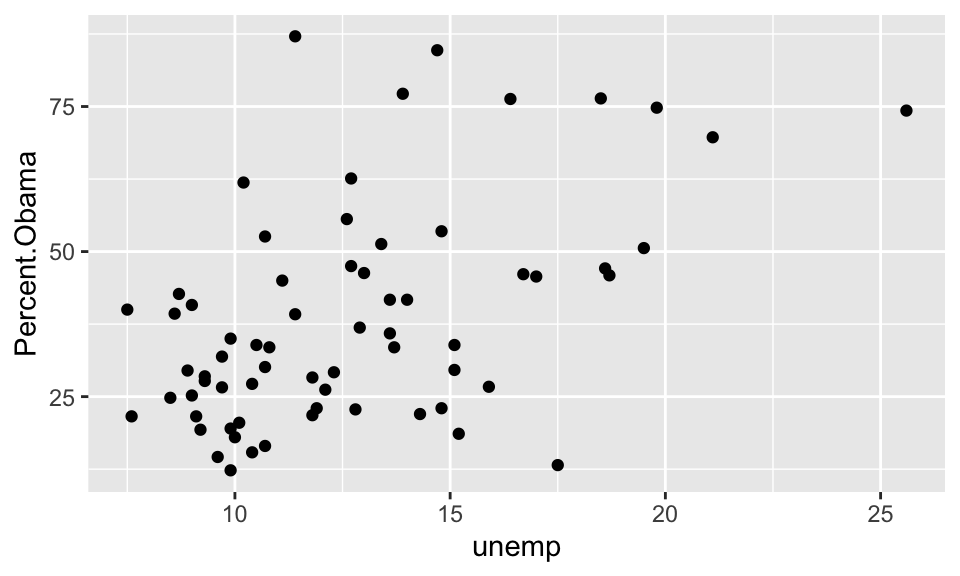

Now, let’s color by the log of population.

## Warning: Removed 1 rows containing missing values (geom_point).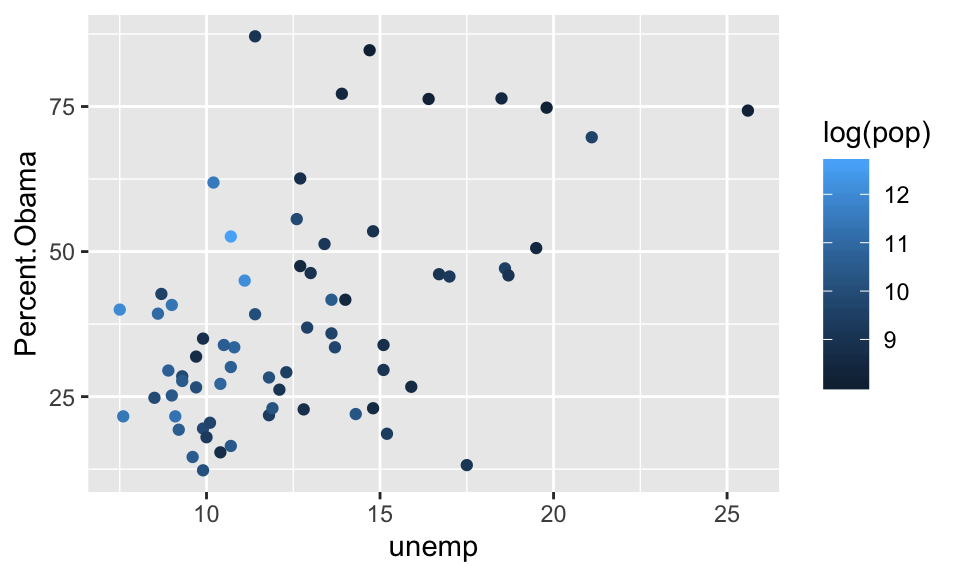

Kind of hard to see what is going on. Let’s try it by having population on the x-axis and coloring by unemployment.

## Warning: Removed 1 rows containing missing values (geom_point).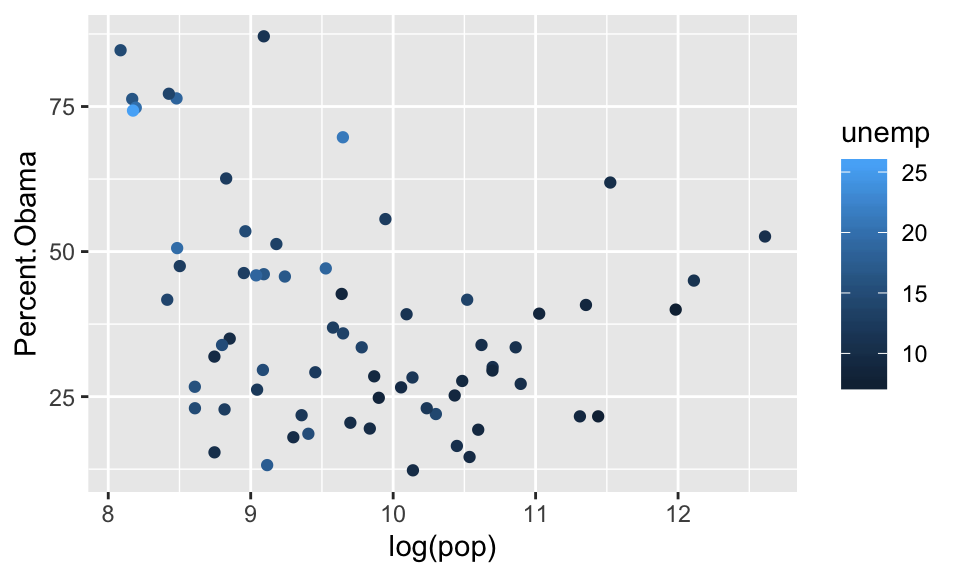

It seems like the smallest and largest counties were more likely to vote Obama, and that counties with higher unemployment were also more likely to vote Obama. However, neither of these plots are particularly compelling.

6.9.1 Some GIS

To get a better idea what is going on with this example, we recall that this data is geographical data. That is, the data comes from specific geographic regions of the state of Alabama. Let’s plot the outcomes of the election on a county map of Alabama, with the counties shaded by “how Obama” they are.

To do this, we need to pull the Alabama county data and store it in a data frame.

Note that this data isn’t organized by FIPS code, so we need to add that and get rid of the variables we won’t be using.

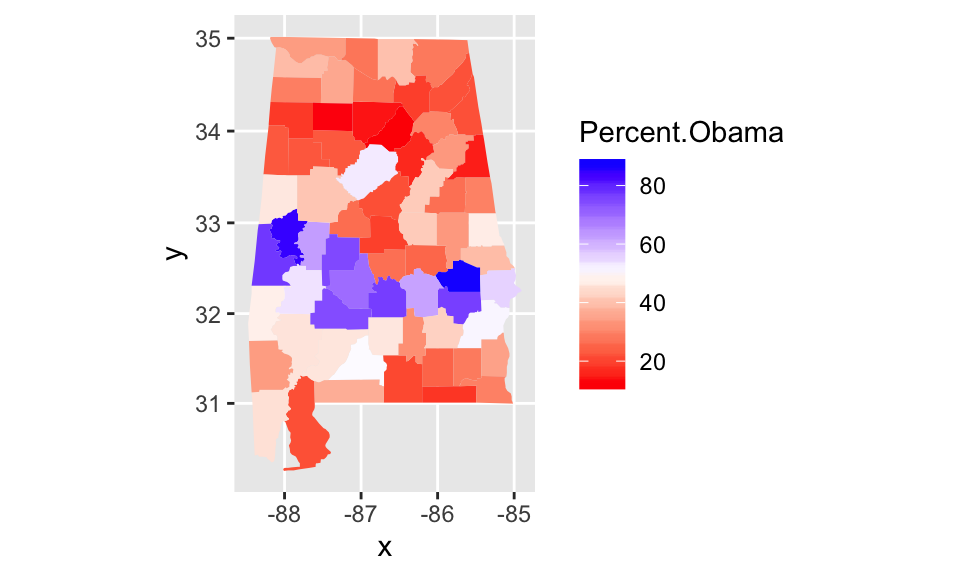
This visualization is more compelling than the previous two: it seems that there is a belt across the middle of Alabama that tended to vote Obama.

6.10 Exercises

  1. The built-in R data set quakes gives the locations of earthquakes off of Fiji in the 1960’s. Create a plot of the locations of these earthquakes, showing depth with color and magnitude with size.

  2. Create a graphic that displays the differences in mpg between 4,6, and 8 cylinder cars in the built-in data set mtcars.

Exercises 3 - 5 all use the Batting data set from the Lahman library. This gives the batting statistics of every player who has played baseball from 1871 through the present day.

    1. Create a scatterplot of the number of doubles hit in each year from 1871-2015.
    2. Create a scatterplot of the number of doubles hit in each year from 1871-2015 in each league. Color the NL blue and the AL red.
  2. Create boxplots for total runs scored per year in the AL and the NL from 1969-2015.
    1. Create a histogram of lifetime batting averages (H/AB) for all players who have at least 1000 career AB’s.
    2. In your histogram from (d), color the NL blue and the AL red. (If a player played in both the AL and NL, count their batting average in each league if they had more than 1000 AB’s in that league.)
     
  4. Use the People data set from the Lahman library.
    1. Create a barplot of the birthmonths of all players. (Hint: geom_bar())
    2. Create a barplot of the birth months of the players born in the USA after 1970.

Exercises 7 - 11 use the babynames data set from the babynames library, which you probably need to install.

  1. Make a line graph showing the total number of babies of each sex, plotted over time.
  2. Make a line graph showing the number of different names used for each sex, plotted over time.
  3. Make a line graph showing how many babies of your gender have your name, plotted over time. If your name doesn’t appear in the data, use the female name “Alexa”.
  4. Make a line graph comparing the number of boys named Bryan and the number of boys named Brian from 1920 to the present.

  5. I wish that I had Jessie’s girl, or maybe Jessie’s guy? One one graph, plot the number of male and female babies named Jessie over time.

    Three time periods show up in the history of Jessie:

    • More male than female Jessie
    • More female than male Jessie
    • About the same male and female Jessie.

    Approximately what range of years does each time period span?

  6. Data scientist Kieran Healy created this widely circulated figure: 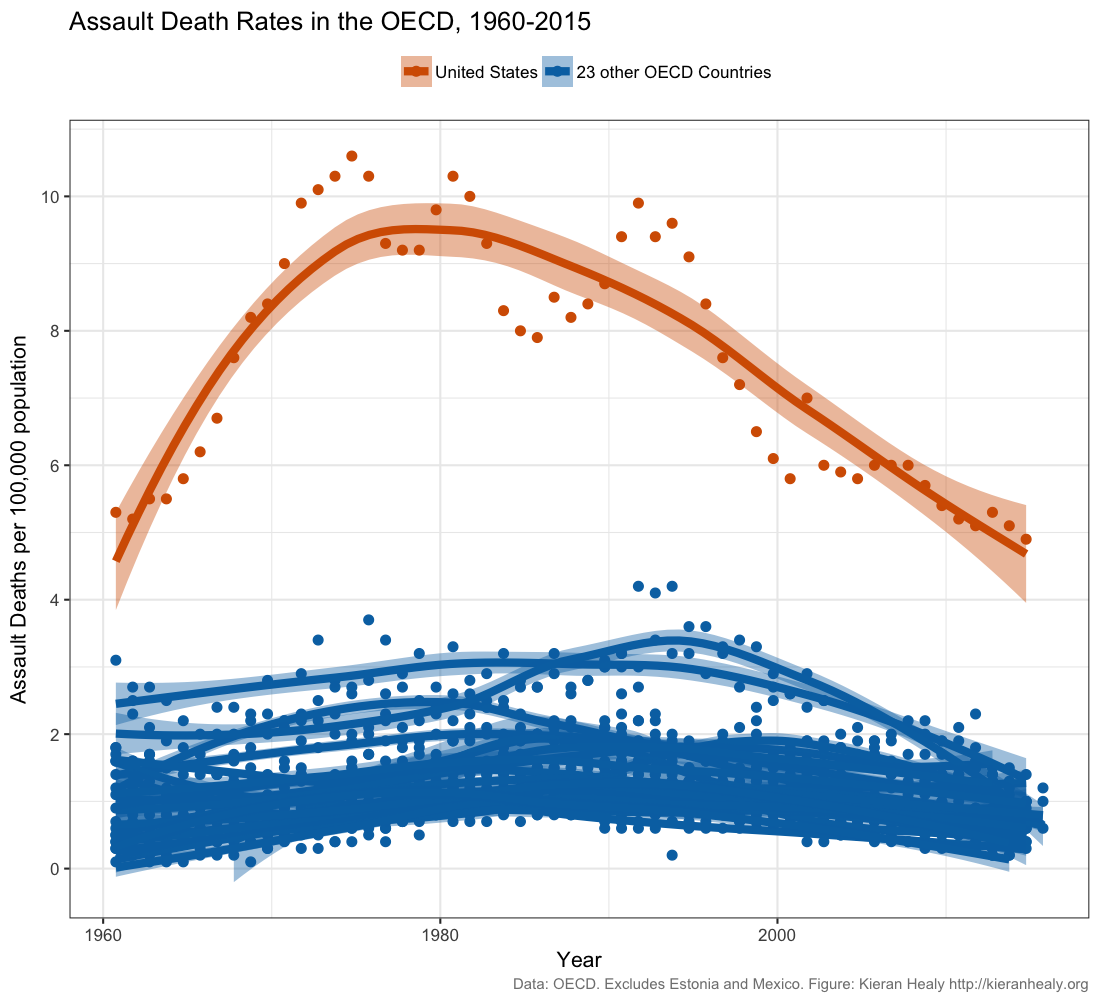Recreate this plot as well as you can, using Healy’s github data. Read Healy’s blog post and his follow up post. Do you think this figure is a reasonable representation of gun violence in the United States?

  1. One of the authors tweeted a clearly wrong reason for the 2, in an attempt to invoke Cunningham’s Law. The author of ggplot2 liked the tweet but did not provide the correct answer, thereby either disproving Cunningham’s Law or confirming that the 2 is to make it sound like “gg plateau”.↩