Chapter 15 Point Estimators

In this chapter, we discuss the theory of point estimation of parameters.

Let \(X_1, \ldots, X_n\) be a random sample from a distribution with real parameter \(\theta.\) We say that \(\hat\theta_n\) is a point estimator for \(\theta\) if \(\hat \theta_n\) is a real-valued function of the random sample \(X_1, \ldots, X_n\). When the context is clear, we will omit the subscript \(n\) and denote \(\hat \theta_n\) as \(\hat \theta\). While in principle any function of the random sample would work, the point estimate of the parameter is to serve as an estimate for the value of the parameter based on the random sample. Therefore, we will be interested in quantifying what it means for a point estimator to be a “good” point estimate for a parameter.

We have already seen several point estimators. The sample mean \(\overline{X} = \frac 1n \sum_{i = 1}^n X_i\) is an estimator for \(\mu\), the mean of the distribution. The sample standard deviation \(S\) is an estimator for \(\sigma\), the standard deviation of a population. The proportion of successes in a fixed number of Bernoulli trials is an estimate for \(p\), the probability of success.

15.1 Sampling distributions of point estimators

We have also already seen some examples of sampling distributions of point estimators. The sampling distribution of \(\hat \theta\) is the probability distribution of \(\hat \theta\), which we often represent as a histogram or density plot. Desirable properties of the sampling distribution of a point estimator include:

  1. The most likely outcome of \(\hat \theta\) is \(\theta\).
  2. The expected value of \(\hat \theta\) is \(\theta\).
  3. The standard deviation of \(\hat \theta\) is small.

Consider below four density functions for an estimator \(\hat \theta\) of \(\theta\). 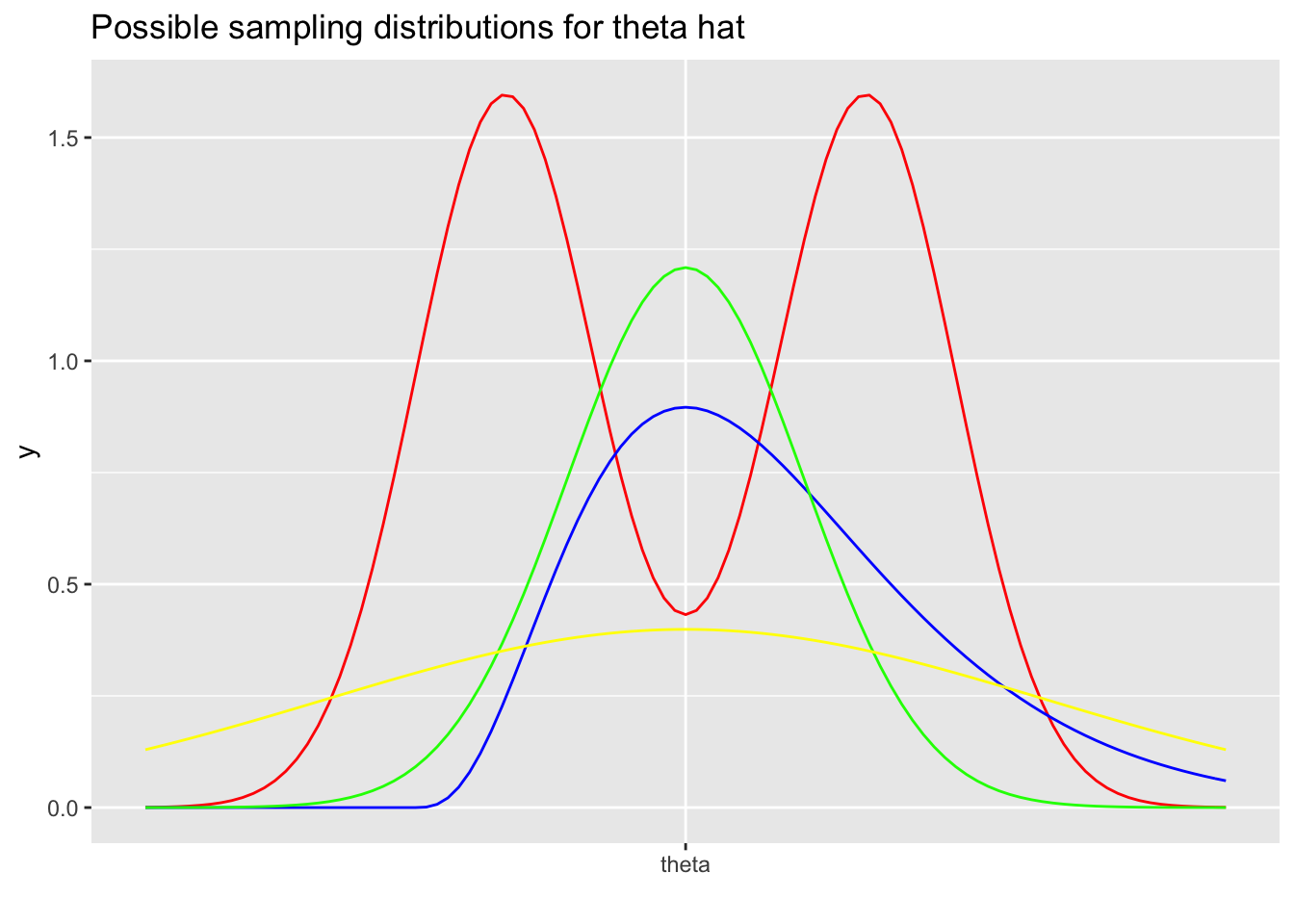In the sampling distributions above, the red estimator has an expected value of \(\theta\), but the most likely values are not \(\theta\). The blue estimator has a most likely value of \(\theta\), but an expected value greater than \(\theta\). The yellow estimator and green estimator both have a most likely value of \(\theta\) and an expected value of \(\theta\), but the standard deviation of the green estimator is smaller than that of the yellow one.

15.2 Bias

In this section, we consider the following phenomenon. Suppose that you are trying to estimate the parameter \(\theta\) using \(\hat \theta\) based on a fixed sample size. If you were to repeat the estimate many times, would it in the limit be the true parameter value?

Definition 2.2 Let \(\hat \theta\) be an estimator for the parameter \(\theta\). We say that \(\hat \theta\) is unbiased if \[ E[\hat \theta] = \theta \] We say that \(\hat \theta\) is asymptotically unbiased if \[ \lim_{n\to \infty} E[\hat \theta] = \theta \]

Example Let \(X_1, \ldots, X_n\) be a random sample from a distribution with mean \(\mu\). Then, the sample mean \(\overline{X}\) is an unbiased estimator for \(\mu\).

We simply compute \[ \begin{aligned} E[\overline{X}] &= \frac 1n E[\sum_{i = 1}^n X_i] \\ &= \frac 1n \sum \mu\\ &=\mu \end{aligned} \]

It is also possible to use simulation to get a good idea of whether a point estimator is an unbiased estimator for a parameter. We would compute the point estimator many times, and take the average value. If we get something close to the true value of the parameter, then the point estimator is likely unbiased. In order to really be sure, we would need to prove it, as above. Simulation also suffers from the drawback that we have to check each distribution and \(n\) separately, so we even if we are relatively confident for the distributions we check, we will not know much (if anything) about new distributions that we have not checked.

Example Use simulation to show that the sample mean is an unbiased estimator for the population mean \(\mu\), when \(X_1, \ldots, X_8\) is a random sample from an exponential random variable with rate 2.

Recall that the mean of an exponential random variable with rate 2 is 1/2. We create a sample of size 8, and compute its mean. Then replicate.

## [1] 0.4981419
## [1] 0.5016221

We see that we get a value close to 1/2. This is evidence that the sample mean is unbiased in this instance. Ideally, we should run the simulation a few times, and see whether we get values on both sides of 1/2. We will see below examples where the bias is very small, but non-zero, and repeating the simulation is a way to check for this.

Let’s also take a look at the sampling distribution of \(\overline{X}\) in this case.

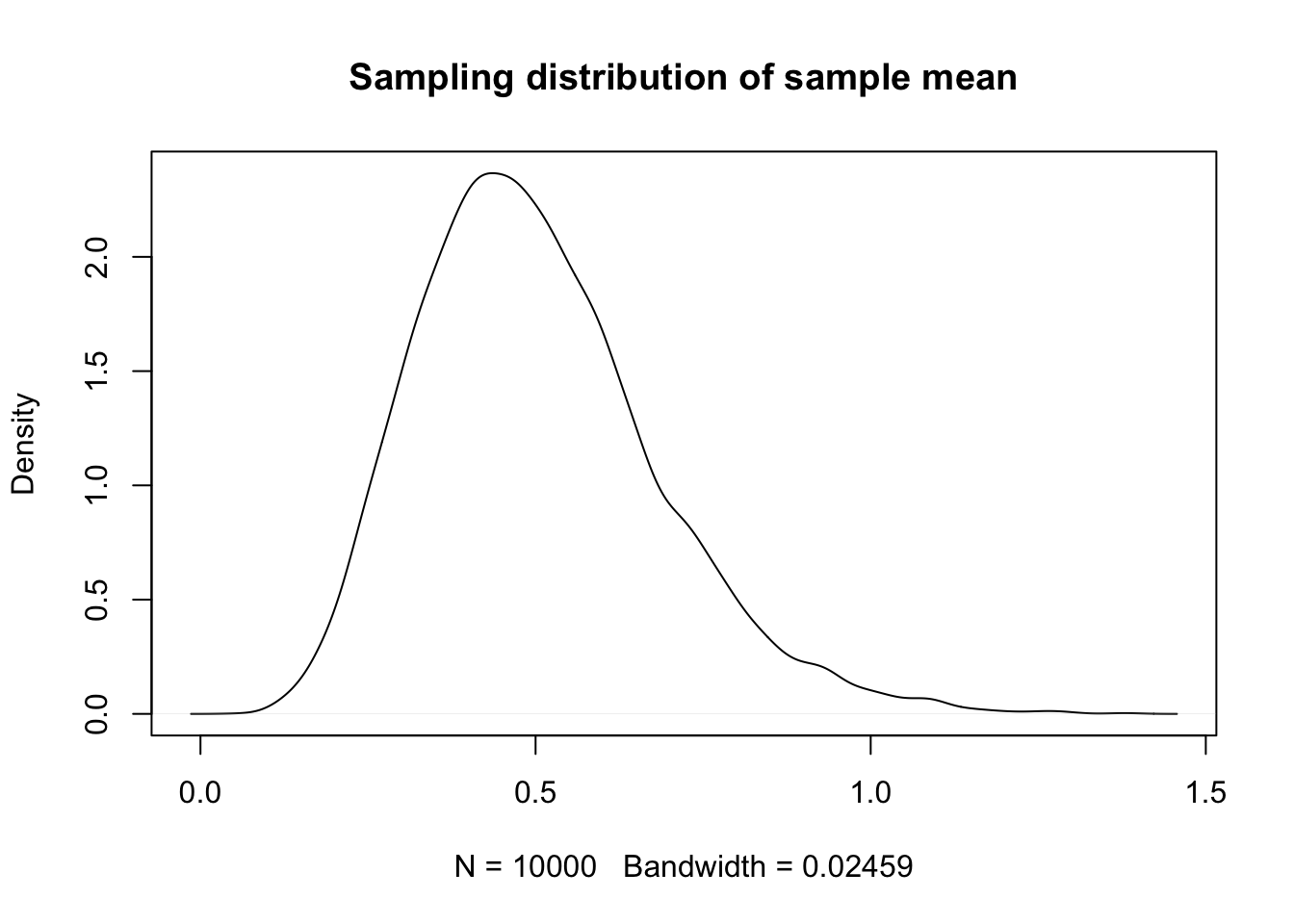We can see that, while the expected value of the point estimator is \(1/2\), the most likely value of \(\overline{X}\) appears to be less than 1/2.

Finally, let’s find the exact distribution of \(\overline{X}\). This isn’t always easy to do, but in this case it follows from the method of moment generating functions. Recall that the sum of \(n\) exponential rvs with rate \(\lambda\) is a gamma random variable with rate \(\lambda\) and scale \(n\). Multiplying a gamma random variable by a constant changes the rate by the inverse of that constant, so \(\overline{X}\) is gamma with scale \(n\) and rate \(n\lambda\); see also exercise ??. Therefore, the expected value of \(\overline{X}\) is \(\frac {n}{n\lambda} = 1/\lambda\), and the most likely outcome of \(\overline{X}\) is \(\frac {n - 1}{n\lambda} = 1/\lambda - 1/(n \lambda) = 1/2 - 1/16\).

Example Let \(X_1, \ldots, X_n\) be a random sample from a distribution with mean \(\mu\) and standard deviation \(\sigma^2\). Show that \[ S^2 = \frac 1{n-1} \sum_{i = 1}^n \bigl(X_i - \overline{X}\bigr)^2 \] is an unbiased estimator for the variance \(\sigma^2\).

The key computation is finding \(E[(X_i - \overline{X})^2]\). We re-write \(X_ i - \overline{X} = \frac {n-1}{n} X_i - \frac {n-1}{n} \overline{X}^*\), where \(\overline{X}^*\) is the sample mean of the \(X_j\) where \(j\not = i\). We recall a few facts.

  1. Note that \(X_i\) and \(\overline{X}^*\) are independent, so \(E[X_i \overline{X}^*] = E[X_i]E[\overline{X}^*]\).
  2. \(E[X_i^2] = \mu^2 + \sigma^2\).
  3. \(E[{\overline{X}^*}{}^2] = \mu^2 + \frac 1{n-1} \sigma^2\).

We have \[ \begin{aligned} E(X_i - \overline{X})^2 &= \bigg(\frac {n-1}{n}\bigg)^2 E(X_i - \overline{X}^*)^2\\ &=\bigg(\frac {n-1}{n}\bigg)^2 \bigl( E[X_i^2] - 2E[X_i]E[\overline{X}^*] + E[{\overline{X}^*}^2]\bigr)\\ &=\bigg(\frac {n-1}{n}\bigg)^2\bigl(\mu^2 + \sigma^2 - 2\mu^2 + \mu^2 + \frac 1{n-1} \sigma^2\bigr)\\ &=\bigg(\frac {n-1}{n}\bigg)^2\frac{n}{n-1} \sigma^2\\ &= \frac{n-1}{n} \sigma^2 \end{aligned} \]

Therefore, \[ \begin{aligned} E[S^2] &= \frac 1{n-1} E[\sum_{i = 1}^n(X_i - \overline{X})^2] \\ &= \frac 1{n-1} \sum_{i = 1}^n \frac{n-1}{n} \sigma^2\\ &= \sigma^2 \end{aligned} \]

We again verify this with simulation for a couple of different cases. First, let \(X_1, \ldots, X_{10}\) be a random sample from an exponential distribution with rate \(\lambda = 2\). (The variance is then \(\frac {1}{\lambda^2}\).) Show that \(S^2\) is an unbiased estimator for \(\sigma^2 = \frac {1}{4}\).

## [1] 0.1049839
## [1] 0.2512457

Again, it is a good idea to repeat the above a few times to see whether we are systematically underestimating or overestimating \(\sigma^2\), which we are not. It is also a good idea to increase the number of replications, to see whether the estimate is getting closer to the true value.

## [1] 0.2502688

Note that the estimates with 100,000 replications are (in general) closer to the true value of 1/4 than the estimates with 10,000 replications.

A common fallacy is to think that if \(\hat \theta\) is an unbiased point estimator for \(\theta\), then \(g(\hat\theta)\) must be an unbiased estimator for \(g(\theta)\). This is almost never true, unless \(g\) is an affine transformation!

Example Show that \(S = \sqrt{\frac{1}{n-1} \sum_{i = 1}^n (X_i - \overline{X})^2}\) is a biased estimator for \(\sigma\) when taking a random sample of size \(10\) from a standard normal distribution.

## [1] 1.16899
## [1] 0.9744921

This is an example where, at first glance, it seems plausible that \(S\) is unbiased. However, if you repeat the above code multiple times, you will see that the mean is consistently under the true value of 1. That is, the expected value of \(S\) is less than \(\sigma = 1\). So, if we use \(S\) to estimate \(\sigma\), we are consistently underestimating it. However, it is true that \(S\) is asymptotically unbiased. We will not prove that, but note that if we take a sample of size 30 rather than 10, then \(S\) is (in general) closer to 1.

## [1] 0.9911216

Note that our estimates for \(\sigma\) are closer to 1 than they were when we only had 10 samples.

Example Let \(X_1, \ldots, X_n\) be a random sample from a uniform distribution on \((0, \theta)\), where \(0 < \theta < \infty\). Show that \(X_{(n)}\) is a biased estimator for \(\theta\), but \(\frac {n + 1}{n} X_{(n)}\) is an unbiased estimator for \(\theta\).

To do this, we let \(Y_i = \frac 1\theta X_i\), so that \(Y_i\) are iid uniform \((0, 1)\) random variables. Then, \(Y_{(n)} = \frac 1\theta X_{(n)}\) has a beta distribution with parameters \(\alpha = n\) and \(\beta = 1\). It follows that \(E[Y_{(n)}] = \frac n{n+1}\), and \(E[\frac{n+1}{n} \frac 1\theta X_{(n)}] = 1\). Pulling out the \(1/\theta\) and bringing to the other side yields the result.

Again, we verify this via simulation. Let’s take a random sample of size 6 from a uniform rv on the interval \((0, 10)\). We look at the maximum value and multiply by 7/6.

## [1] 11.63385
## [1] 9.99694

Example Let \(X_1, \ldots, X_n\) be a random sample from an exponential distribution with rate \(\lambda\). Find an unbiased estimator for the second moment \(E[X^2]\).

We will use a guess-and-check method to do this. We know that \(E[X^2] = \mu^2 + \sigma^2 = 2/\lambda^2\). We also know that \(\overline{X}\) is an unbiased estimator for \(1/\lambda\). So, we guess, knowing that it will almost certainly be wrong, that \(2 \overline{X}^2\) will be an unbiased estimator for \(E[X^2]\). Now, recall that the variance of \(\overline{X}\) is \(\frac 1n \sigma^2\), where \(\sigma^2 = 1/\lambda^2\). Therefore, \[ \begin{aligned} E[(\overline{X})^2] &= \mu^2 + \frac 1n \sigma^2\\ &=\frac {1}{\lambda^2} + \frac {1}{n\lambda^2}\\ &=\frac {n + 1}{n} \frac{1}\lambda^2 \end{aligned} \] This implies that \(2\frac{n}{n+1} \overline{X}^2\) is an unbiased estimator for \(E[X^2]\).

We confirm this via simulations, choosing \(n = 9\) and \(\lambda = 1/3\).

## [1] 9.910037
## [1] 18.10206

We see that we get approximately \(2/\lambda^2 = 18\), as desired.

15.3 Consistency

Definition 15.1 A point estimator \(\hat \theta\) for \(\theta\) is said to be consistent if for every \(\epsilon > 0\), \[ \lim_{n\to\infty} P(|\hat \theta - \theta| > \epsilon) = 0 \]

This says that given any tolerance, there is a sample size large enough so that the probability that the point estimator is off by more than the tolerance is extremely small. It may seem like this is saying something very similar to being unbiased, or possible asymptotically unbiased. That relationship is explored in the next theorem.

Theorem 15.1 If \(\hat\theta\) is unbiased and \(V(\hat\theta) \to 0\) as \(n\to\infty\), then \(\hat\theta\) is consistent.
Proof. The proof makes use of Chebychev’s Theorem, which says that for any random variable \(X\) with standard deviation \(\sigma\), \[ P(|X - E[X]| \ge k\sigma) \le 1/k^2. \] Since \(P(|X - E[X]| > k \sigma) \le P(|X - E[X]| \ge k\sigma)\), it is also true that \[ P(|X - E[X]| > k\sigma) \le 1/k^2. \] Since \(\hat \theta\) is unbiased, we have that \(E[\hat\theta] = \theta\), and we apply Chebychev’s Theroem to \(\hat \theta\). We obtain \[ \begin{aligned} P(|\hat\theta - \theta| > \epsilon) &= P(|\hat\theta - \theta| > \frac{\epsilon}{\sigma_{\hat\theta}} \sigma_{\hat \theta} )\\ &\le \frac{\sigma_{\hat \theta}^2}{\epsilon^2} \to 0 \end{aligned} \] as \(n\to \infty\) by the assumption that the variances of \(\hat \sigma\) go to zero.

We will improve this theorem below where we show that if an estimator is asymptotically unbiased and the variance goes to zero, then the estimator is also consistent.

Example Let \(X_1, \ldots, X_n\) be a random sample from a distribution with mean \(\mu\) and standard deviation \(\sigma\). The sample mean \(\overline{X}\) is a consistent estimator of \(\mu\).

We wish to apply the previous theorem. We have already seen that \(\overline{X}\) is unbiased; now we need to see that its variance goes to zero as \(n\to\infty\). Indeed, the variance of \(\overline{X}\) is \(\sigma^2/n\), which goes to zero as \(n\to\infty\).

Most “good” point estimators that we encounter will be consistent. Two ways that a point estimator may fail to be consistent are:

  1. If a point estimator is not asymptotically unbiased, then it is very likely not consistent. (However, see exercise ??)
  2. If a point estimator only uses a finite number of samples, then it is very likely not consistent.

For example, if we let \(X_1, \ldots, X_n\) be a random sample from an exponential distribution and we estimate \(\hat \mu = X_1\), then \(E[\hat \mu] = \mu = 1/\lambda\), so \(\hat \mu\) is unbiased. However, for \(\epsilon = \mu\), \(P(|\hat \mu - \mu| > \epsilon) = P(X_1 > 2\mu)\). Since this is a non-zero constant, it certainly doesn’t converge to 0 and \(\hat \mu\) is not consistent.

It is possible to get an idea whether an estimator is consistent via simulations, though this is again not the same as a proof. We can choose several values of \(\epsilon\), and see whether it appears that there are large enough \(n\) such that \(P(|\hat \theta - \theta| > \epsilon)\) is small. When we are doing simulations with 10,000 runs, this would mean that, perhaps 0-2 of the 10,000 runs have values \(|\hat \theta - \theta| > \epsilon\).

Example Provide evidence via simulation that the sample mean is consistent for the population mean when sampling from a normal distribution.

We fix \(\mu = 1\) and \(\sigma = 2\), and we show that for \(\epsilon = 1\), \(\epsilon = 0.1\) and \(\epsilon = 0.01\), we can find \(n\) such that our estimate for \(P(|\overline{X} - 1| > \epsilon) < 2/10,000\).

We show in detail the case when \(\epsilon = .1\). We start with \(N = 100\) and see if that is big enough.

## [1] 0.6217

We see \(N = 100\) is not nearly large enough. Let’s double it.

## [1] 0.4752

Our estimate for \(P(|\overline{X} - 1| > .1)\) is now 0.4772, still too big. Let’s double \(N\) again.

## [1] 0.3137

Still too large, but it seems to be getting smaller as \(N\) is getting bigger. If an estimator is consistent, then this value should keep getting smaller on balance until in the limit it is zero. Let’s repeat the estimates of probability above for \(N = 100, 200, 500, 1000, 2000, 5000, 10000\) all in one chunk, and examine the probabilities. You can either run the above code multiple times and keep track of the values, or you can wrap everything inside of sapply as below. This chunk of R code can take a bit of time to run.

N Prob
100 0.6187
200 0.4820
500 0.2646
1000 0.1101
2000 0.0251
5000 0.0002
10000 0.0000

The table above is a typical type of table that we would get when an estimator is consistent. The probability is decreasing until eventually it is less than 0.0001, which is the smallest probability that we can estimate with a replication size of 10,000.

15.4 Likelihood Functions and Sufficiency

When we are taking a random sample from a distribution, whether it is discrete or continuous, we are often interested in how likely a given combination of values is.
Definition 15.2 Let \(X_1, \ldots, X_n\) be a random sample from a common distribution with pdf \(f\) or pmf \(p\). We define the likelihood function in the case of a continuous distribution as \[ L(x_1, \ldots, x_n) = \prod_{i = 1}^n f(x_i) \] and in the case of a discrete distribution we define it as \[ L(x_1, \ldots, x_n) = \prod_{i = 1}^n p(x_i) \]

Let’s look at a few examples of computing likelihood functions.

Example Let \(X_1, \ldots, X_n\) be a random sample from an exponential distribution with rate \(\lambda\). Find the likelihood function.

Here, we have \[ \begin{aligned} L(x_1, \ldots, x_n) &= \prod_{i = 1}^n f(x_i)\\ &=\prod_{i = 1}^n \lambda e^{-\lambda x_i}\\ &=\lambda^n e^{-\lambda \sum_{i = 1}^n x_i} \end{aligned} \] Note that this is correct when all of the \(x_i\) are positive. If one or more of the \(x_i\) are negative, then the likelihood function is zero.

Example Let \(X_1, \ldots, X_n\) be a random sample from a Poisson distribution with mean \(\lambda\). Find the likelihood function.

Here, we have \[ \begin{aligned} L(x_1, \ldots, x_n) &= \prod_{i = 1}^n p(x_i)\\ &=\prod_{i = 1}^n \frac{\lambda^{x_i}}{x_i!} e^{-\lambda} \\ &=e^{-n\lambda} \frac{\lambda^{\sum_{i = 1}^n x_i}}{\prod_{i = 1}^n x_i!} \end{aligned} \]

In the first example above, we played fast and loose with bounds. Let’s look carefully at how we can deal with pdfs of this type. Let \(E\) be a subset of the real numbers. We define \[ I_E(x) = \begin{cases} 1 & x \in E\\ 0 & x\not\in E \end{cases} \] We have \(I_E(x) \times I_G(x) = I_{E \cap G}(x)\), and most importantly for our purposes in this chapter: \(I_{(-\infty, b)}(x) \times I_{(-\infty, b)}(y)\) is 1 if and only if both \(x\) and \(y\) are less than \(b\). In other words, it is 1 if and only if the maximum of the two is less than \(b\). We summarize this and other important facts about indicator functions in the following theorem.

Theorem 15.2 Let \(a, b, x\) and \(y\) be real numbers.

  1. \(I_{(-\infty, b)}(x) \times I_{(-\infty, b)}(y) = I_{(-\infty, b)}(\max(x, y))\)

  2. \(I_{(a, \infty)}(x) \times I_{(a, \infty)}(y) = I_{(a, \infty)}(\min(x, y))\)

  3. \(I_{(a, \infty)}(x) \times I_{(-\infty, b)}(x) = I_{(a, b)}(x)\)

Example Let \(X_1, \ldots, X_n\) be a random sample from an exponential distribution with rate \(\lambda\). Find the likelihood function.

To do this properly, we note that the full pdf of an exponential random variable can be written as \(f(x) = \lambda e^{-\lambda x} I_{[0, \infty)}(x)\). We have \[ \begin{aligned} L(x_1, \ldots, x_n) &= \prod_{i = 1}^n f(x_i)\\ &=\prod_{i = 1}^n \lambda e^{-\lambda x_i}I_{[0, \infty)}(x_i)\\ &=\lambda^n e^{-\lambda \sum_{i = 1}^n x_i}I_{[0, \infty)}(x_{(1)}) \end{aligned} \] where \(I_{[0, \infty)}(x_{(1)})\) is 1 if the minimum of the \(x_i\) is zero or larger, and zero otherwise.

Example Let \(X_1, \ldots, X_n\) be a random sample from a uniform distribution on the interval \([0, \theta]\). Find the likelihood function.

Again, we write out the pdf of a uniform random variable on the interval \([0, \theta]\) in the new notation as \(f(x) = \frac 1\theta I_{(-\infty. \theta]}(x) I_{[0, \infty)}(x)\), where \(\theta > 0\). We compute the likelihood function as \[ \begin{aligned} L(x_1, \ldots, x_n) &= \prod_{i = 1}^n f(x_i)\\ &=\prod_{i = 1}^n \frac 1\theta I_{(-\infty. \theta]}(x_i) I_{[0, \infty)}(x_i)\\ &=\frac 1{\theta^n} I_{(-\infty. \theta]}(x_{(n)}) I_{[0, \infty)}(x_{(1)}) \end{aligned} \] In other words, the likelihood function is \(\frac 1{\theta^n}\) if all of the \(x_i\) are between 0 and \(\theta\), and zero otherwise.

When estimating a parameter \(\theta\) via a summary statistic of the data, one might wonder whether one is using all of the information available from the sample. For example, when we estimate the mean of a distribution \(\mu\) via the sample mean \(\overline{X}\) when sampling from a normal distribution, would we be able to improve the estimate for \(\mu\) by also considering the median of the sample? Intuitively, a statistic is sufficient if knowing the value of the individual samples gives no additional information for estimating the parameter than knowing the value of the statistic.

Definition 15.3 Let \(X_1, \ldots, X_n\) be a random sample from a distribution with parameter \(\theta\). Let \(T(X_1, \ldots, X_n)\) be a real valued function of \(X_1, \ldots, X_n\). We say that \(T\) is sufficient for \(\theta\) if the distribution of \(X_1, \ldots, X_n\) given the value of \(T\) does not depend on \(\theta\).

By the factorization criterion of independence, we have the following.

Theorem 15.3 Let \(X_1, \ldots, X_n\) be a random sample from a distribution with parameter \(\theta\). Let \(T(X_1, \ldots, X_n)\) be a real valued function of \(X_1, \ldots, X_n\). Let \(L(x_1, \ldots, x_n)\) be the likelihood function of \(X_1, \ldots, X_n\). \(T\) is sufficient for \(\theta\) if there exists functions \(g(T, \theta)\) and \(h(x_1, \ldots, x_n)\) such that \[ L(x_1, \ldots, x_n) = g(T, \theta) h(x_1, \ldots, x_n) \]

The key to the above theorem is that \(g\) only depends on \(x_1, \ldots, x_n\) via the statistic \(T\).

Example Show that \(\overline{X}\) is sufficient for \(\lambda\) when sampling from an exponential distribution.

From above, we know that the likelihood function is \[ \begin{aligned} L(x_1, \ldots, x_n) &= \lambda^n e^{-\lambda \sum_{i=1}^n x_i}\\ \lambda^n e^{-\lambda n \overline{x}} \end{aligned} \] which is factored in the appropriate form with \(h = 1\).

Example Show that \(X_{(n)}\), the maximum, is sufficient for \(\theta\) when sampling from a uniform distribution on the interval \([0, \theta]\).

From above, we know that the likelihood function is \[ L(x_1, \ldots, x_n) = \frac 1{\theta^n} I_{(-\infty. \theta]}(x_{(n)}) I_{[0, \infty)}(x_{(1)}) \] which is factored in the appropriate form with \(h = \frac 1{\theta^n} I_{[0, \infty)}(x_{(1)})\).

15.5 MVUE

A point estimator \(\hat \theta\) for a parameter \(\theta\) is said to be an MVUE (Minimum Variance Unbiased Estimator) of \(\theta\) if

  1. \(\hat \theta\) is an unbiased estimator of \(\theta\), and
  2. whenever \(\hat \theta_2\) is an unbiased estimator of \(\theta\), \(V(\hat \theta_2) \ge V(\hat \theta)\).
The main theoretical result is the Lehmann-Scheffe Theorem.
Theorem 15.4 Let \(\hat \theta\) be an unbiased, sufficient and complete estimator of \(\theta\). Then, \(\hat \theta\) is an MVUE of \(\theta\).

We have already seen unbiased and sufficient estimators, but the Lehmann-Scheffe Theorem also requires the estimator to be complete. An estimator \(T\) is said to be complete for the parameter \(\theta\) if the only function \(g\) such that \(E[g(T)] = 0\) for all \(\theta\) is the zero function. Let’s look at a couple of examples.

Example Let \(X_1, \ldots, X_n\) be a random sample from a normal distribution with mean \(\mu\) and standard deviation 1. Show that the ordered pair \((X_1, X_2)\) is not complete for \(\mu\).

We need to find a function of \(X_1\) and \(X_2\) that has expected value of zero, but is not the zero function. Let \(g(X_1, X_2) = X_1 - X_2\) and see that \(E[g(X_1, X_2)] = 0\) for all values of \(\mu\), but \(g\) is not identically the zero function.

Example let \(X\) be a random sample of size 1 from a uniform distribution on \([0, \theta]\). Show that \(X\) is complete for \(\theta > 0\).

We will not show this to the end, as it is beyond the scope of this book. However, let’s see what we would have to do. Let \(g\) be a function of \(X\) such that \(E[g(X)] = 0\) for all \(\theta > 0\). That is, for all \(\theta > 0\), \[ E[g(X)] = \int_0^\theta \frac 1\theta g(x) \, dx = 0, \] which means \(\int_0^\theta g(x) \, dx = 0\) for all \(\theta\). Therefore, letting \(\theta_1 < \theta_2\) be arbitrary, we have \[ \int_0^{\theta_2} g(x) \, dx - \int_{0}^{\theta_1} g(x)\, dx = \int_{\theta_1}^{\theta_2} g(x)\, dx = 0 \] If we assume, in addition, that \(g\) is continuous, then we can complete the proof. Suppose for the sake of contradiction that there exists an \(x_0\) such that \(g(x_0) \not= 0\). We assume without loss of generality that \(g(x_0) > 0\). Then, there exists a small interval containing \(x_0\) such that \(g(x) > g(x_0)/2\) on the entire interval. We write that interval as \((\theta_1, \theta_2)\), and we see that \[ \int_{\theta_1}^{\theta_2} g(x)\, dx \ge (\theta_2 - \theta_1)g(x_0)/2, \] a contradiction.

For the purposes of this book, when talking about MVUE’s, we will only provide statistics that are complete, and you will not need to prove that they are complete to apply Lehmann-Scheffe.

Example Let \(X_1, \ldots, X_n\) be a random sample from an exponential random variable with rate \(\lambda\). Assume that \(\overline{X}\) is complete for \(\lambda\) and show that \(\overline{X}\) is an MVUE for \(1/\lambda\).

First, we note that \(E[\overline{X}] = 1/\lambda\), so it is unbiased. We showed above that \(\overline{X}\) is sufficient, and we assume that it is complete. Therefore, by Lehmann-Scheffe, \(\overline{X}\) is an MVUE for \(1/\lambda\).

Example Let \(X_1, \ldots, X_n\) be a random sample from a uniform distribution on the interval \([0, \theta]\). Assume that \(X_{(n)}\) is complete for \(\theta\) and show that \(\frac {n+1}{n} X_{(n)}\) is an MVUE for \(\theta\).

Example To do: find an example with a pdf that works out nicely from start to finish.

If \(X_1, \ldots, X_n\) is a random sample from a uniform distribution on \([0, \theta]\), then we have seen that \(X_{(n)}\) is an MVUE. Let’s estimate the variance in the case that \(n = 10\) and \(\theta = 20\), and compare that to the variance of the unbiased estimator \(2 \overline{X}\) via simulations.

We begin by estimating the variance of the MVUE:

## [1] 3.372564

Next, we estimate the variance of \(2\overline{X}\).

## [1] 13.48041

We see that there is quite a large difference in the estimates of the variance! From a practical point of view, this is an indication that \(\frac {n+1}{n} X_{(n)}\) is preferred as an estimator for \(\theta\) over \(2\overline{X}\), because for any individual sample, we would expect that the value of \(\frac {n+1}{n} X_{(n)}\) would be closer to the true value of \(\theta\) than the value of \(2\overline{X}\) would be. For example, in the above simulations, let’s compute the percentage of times that the estimate is within 0.5 of the correct value.

## [1] 0.1901
## [1] 0.1094

We see that the MVUE is within .5 of the correct value twice as often as \(2\overline{X}\) is.

15.6 MSE

It is tempting to think that, once we have MVUE’s, that is the end of story. What type of estimator could be better than, or even competitive with, the unbiased estimator with the smallest variance? We should be careful making claims about “best”, though 17. If we change the thing we are optimizing a bit, then “best” can mean something different. In this section, we discuss the MSE (mean-squared error) of an estimator.

Definition 15.4 Let \(\hat \theta\) be an estimator for \(\theta\) based on a random sample from \(X_1, \ldots, X_n\) from a distribution with parameter \(\theta\). The MSE of \(\hat \theta\) is defined to be \[ MSE(\hat\theta) = E[(\hat \theta - \theta)^2] \]

Theorem 4.1 Let \(\hat \theta\) be an estimator for \(\theta\) based on a random sample from \(X_1, \ldots, X_n\) from a distribution with parameter \(\theta\). Let \(B(\hat\theta)\) denote the bias of \(\hat \theta\); that is, \(E[(\hat \theta - \theta)]\). Then, \[ MSE(\hat\theta) = V(\hat\theta) + \bigl(B(\hat\theta)\bigr)^2 \]

That is, the MSE of a point estimator is the sum of the variance of the estimator and the bias squared of the estimator. In particular, for an unbiased estimator, the MSE is just the variance of the estimator.

Example Find the MSE of \(\overline{X}\) when estimating \(\mu\) when sampling from a distribution with mean \(\mu\) and standard deviation \(\sigma\).

Since \(\overline{X}\) is unbiased, the answer is \(V(\overline{X}) = \sigma^2/n\).

Example Determine whether \(\frac {n+1}{n} X_{(n)}\) or \(\frac {n + 1/2}{n} X_{(n)}\) has a smaller MSE of \(\theta\) when taking a sample of size 3 from a uniform distribution on \([0, \theta]\) when \(\theta = 10\).

Let’s do this first via simulation.

## [1] 6.717689
## [1] 6.453121

While similar, the MSE of the non MVUE is lower than that of the MVUE. We are able to trade some increase in bias for a correspondingly larger decrease in variance, which allows the MSE to be smaller. You are asked to fill in the details of computing the MSE exactly in each case in an exercise. The outline is that \(\frac 1{10}X_{(3)}\) is beta with \(\alpha = 3\) and \(\beta = 1\). Therefore, \(V(\frac 1{10} X_{(3)}) = .0375\). This means that \(V(X_{(3)}) = 3.75\), so \(MSE(\frac 43 X_{(3)}) = V(4/3 X_{(3)}) = 16/9 * 3.75 = 6.666\). A similar argument, which also takes into account the bias shows that \(MSE(\frac {3.6}{3} X_{(3)}) = 5.4 + 1^2 = 6.4\).

Example Assume we have a random sample of size \(n\) from a normal distribution with mean 1 and standard deviation 2.

1.Show via simulation that \(\frac 1n \sum_{i = 1}^n (x_i - \overline{x})^2\) has a lower MSE when estimating \(\sigma^2\) than \(S^2\) does when \(n = 6\).

  1. Estimate the constant \(A\) such that \(\frac 1{n + A} \sum_{i = 1}^n (x_i - \overline{x})^2\) has minimum MSE for \(n = 6\).

We begin by computing the MSE’s for the two point estimates. The one corresponding to \(\frac 1n\) is considerably smaller.

## [1] 6.466083
## [1] 4.861485

Now, in order to try to find the best constant \(A\), we will use sapply and repeat the above computations for several values of \(A\). After a bit of trial and error, we determined that \(-1 \le A \le 3\).

## [1] 1.122449

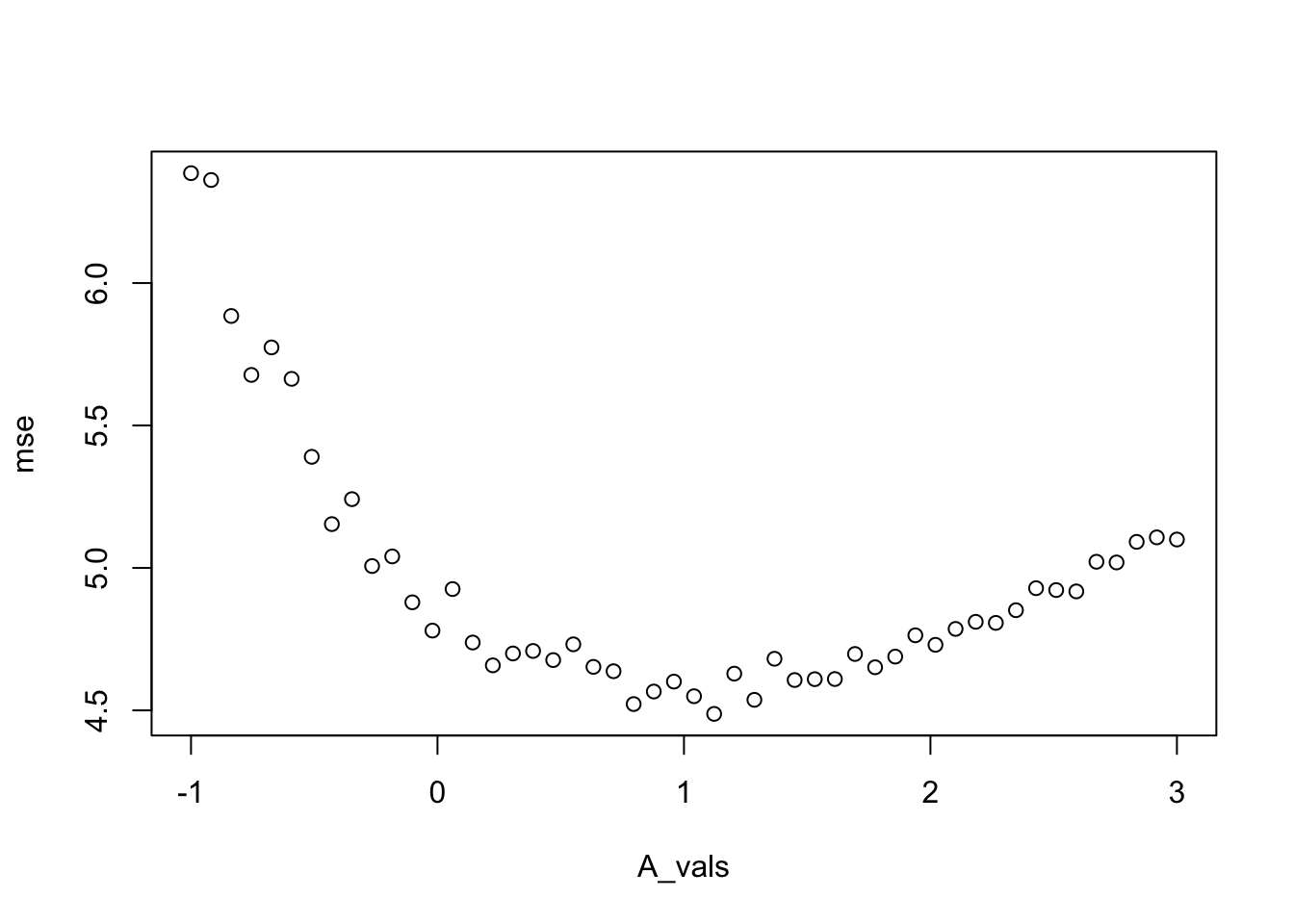
Based on this plot, it appears that a value of \(A = 1\) yields approximately the best MSE when estimating \(\sigma^2\). However, we can also see that there isn’t a lot to choose from for \(0 \le A \le 2\), as those values all yield an MSE of about 4.5.

15.7 Method of Moments

In the previous sections, we primarily discussed properties of point estimators. The only suggestion for how to find a point estimator was for MVUE’s, where it was suggested to find a function of a sufficient statistic that is unbiased. In this and the next section, we discuss two additional methods for creating point estimators.

The method of moments works as follows. Let \(X_1, \ldots, X_n\) be a random sample from a distribution with parameters \(\theta_1, \ldots, \theta_m\). We define the \(k\)th sample moment as \[ \mu_k = \frac 1n \sum_{i = 1}^n X_i^k. \] The \(k\)th moment is given by \(m_k = E[X^k]\), where \(X\) is a random variable with the same distribution as \(X_1, \ldots, X_n\). For the method of moments, we equate the first \(m\) sample moments with the first \(m\) moments, and solve for the parameters in terms of the moments.

Example Let \(X_1, \ldots, X_n\) be a random sample from an exponential distribution with rate \(\lambda\). Find the method of moments estimator for \(\lambda\).

The first moment of an exponential rv with rate \(\lambda\) is \(E[X] = 1/\lambda\). We equate this with the first sample moment and solve for \(\lambda\). Therefore, \(1/\hat\lambda = \overline{X}\), or \(\hat \lambda = 1/\overline{X}\).

Let’s test via simulation whether this is an unbiased and/or consistent estimator of \(1/\lambda\) when \(\lambda = 2\).

## [1] 2.219611

Running the above computation a few times is convincing evidence that \(1/\overline{X}\) is a biased estimator of \(\lambda\) when \(n = 2\). Next, we see whether it appears to be consistent. We choose \(\epsilon = .05\) in the definition of consistency and see whether, as the sample size goes to infinity, it appears that \(P(|1/\overline{X} - 2| > .05) \to 0\).

##  [1] 0.9407 0.9112 0.8621 0.7974 0.7272 0.5746 0.4270 0.2643 0.0780 0.0130

While not completely convincing perhaps, this is evidence that the limit is indeed zero, and that the method of moments estimator is consistent.

Example Let \(X_1, \ldots, X_n\) be a random sample from a normal distribution with mean \(\mu\) and standard deviation \(\sigma\). Find the method of moments estimators for \(\mu\) and \(\sigma\).

The first moment is \(\mu\) and the second moment is \(E[X^2] = \mu^2 + \sigma^2\). Therefore, we have \(\hat \mu = \overline{X}\) and \[ \frac 1n \sum_{i = 1}^n X_i ^2 = \overline{X}^2 + \hat \sigma^2 \] so \[ \hat \sigma^2 = \frac 1n \sum_{i = 1}^n X_i ^2 - \overline{X}^2. \]

Let’s run some simulations. Assume we have a sample of size 20 from a normal distribution with mean 1 and variance 4. Find the method of moments estimators for \(\mu\) and \(\sigma\).

## [1] 0.8568755
## [1] 2.227968

These estimates are not always particularly close to the true values. But, let’s see what the sampling distribution of the estimators is.

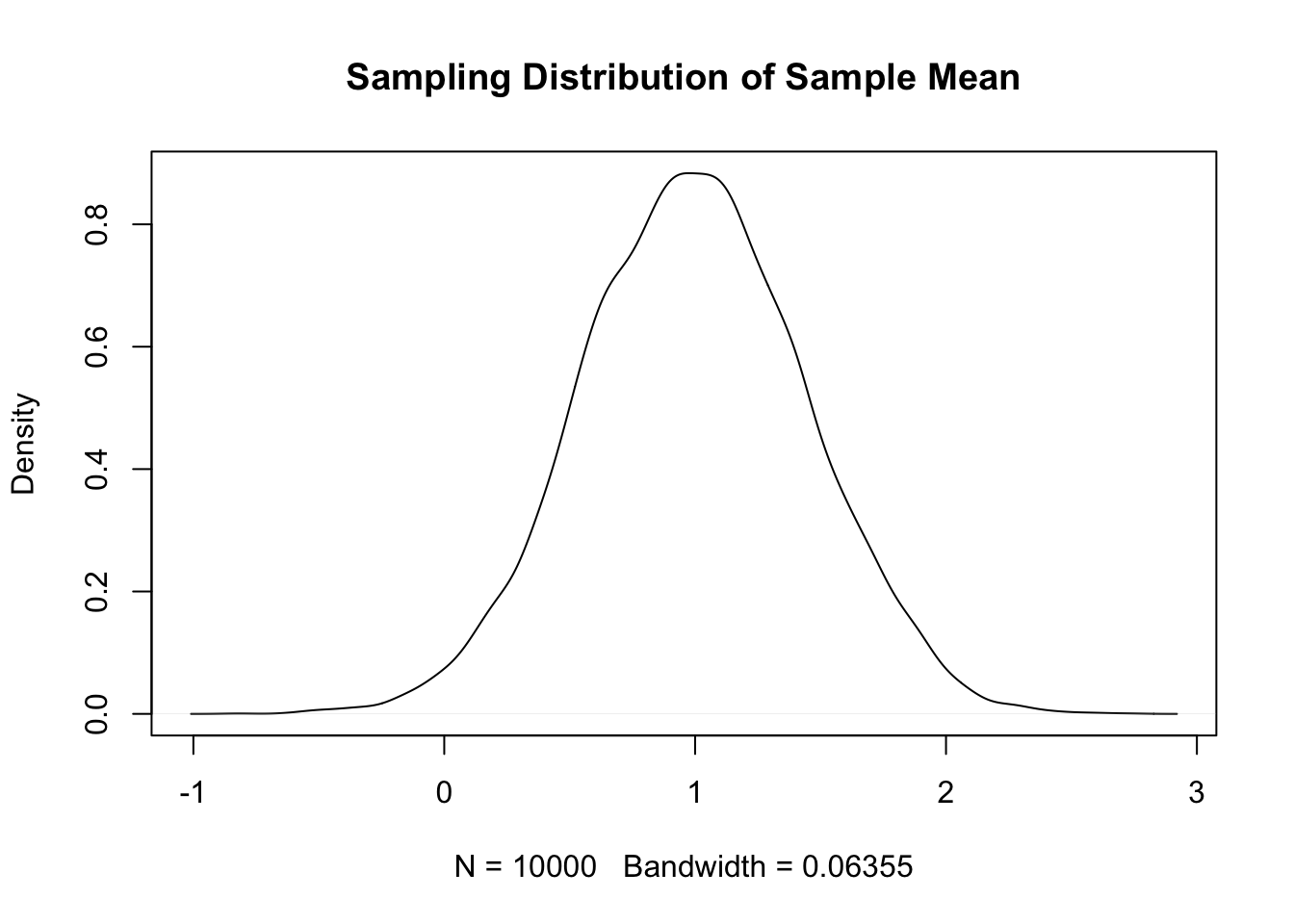
We see that the sampling distribution of the sample mean is centered around \(\mu = 1\), which is the true value.

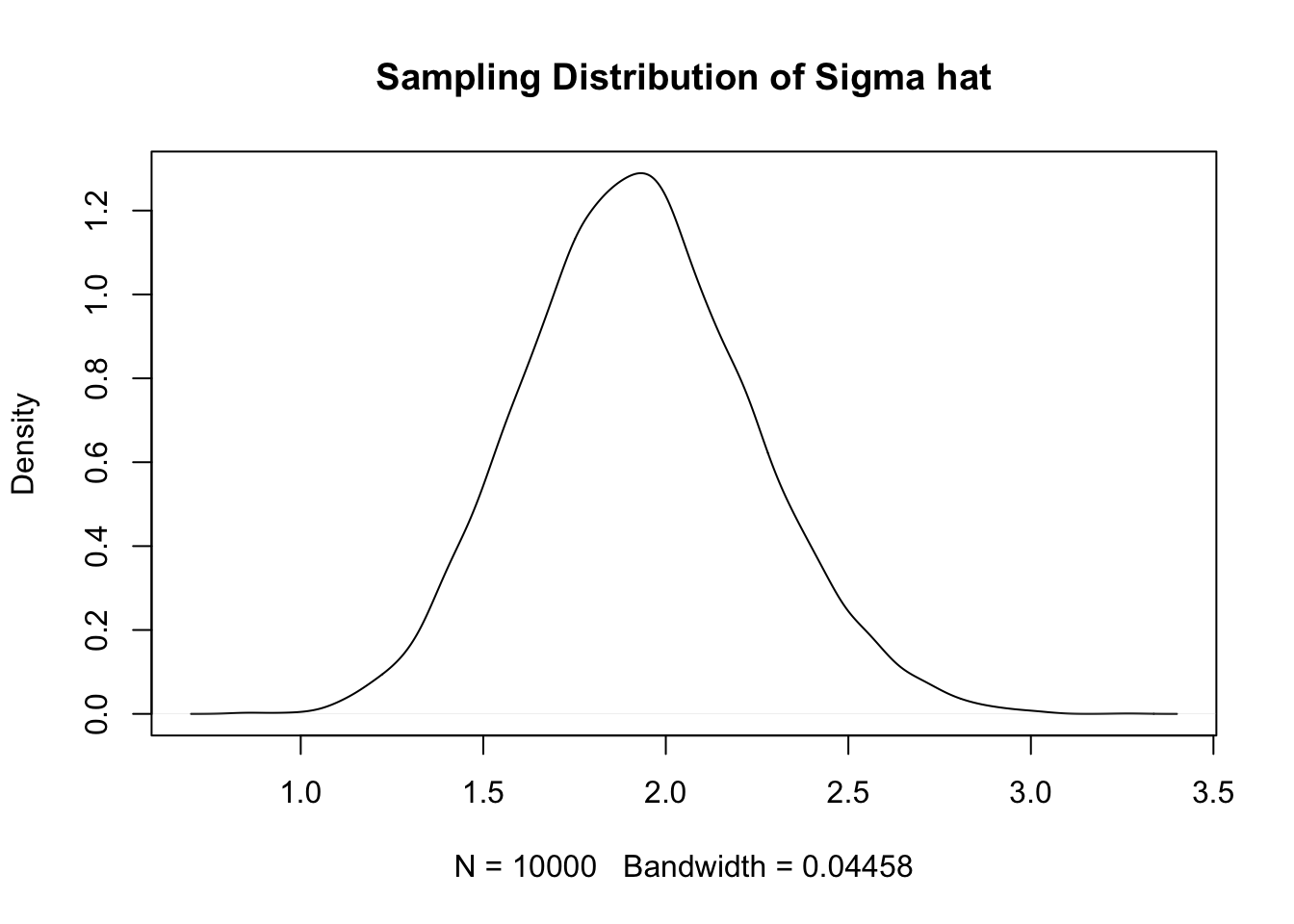
Here, we see that the most likely value of \(\hat \sigma\) appears to be slightly less than the true value of 2. It also appears to be biased.

15.8 Maximum Likelihood Estimators

Recall that the likelihood function is given by \(L(x_1, \ldots, x_n) = \prod_{i = 1}^n f(x_i)\). The likelihood of a sample also has a dependence on the parameter values of the distribution. The maximum likelihood estimator (MLE) of a parameter is the value of the parameter that maximizes the likelihood function. That is, it is the value of the parameter that makes the sample that was observed the most likely from among all possible parameter values.

In practice, it is often easier to maximize the log of the likelihood function, since logs convert products to sums, which makes taking derivatives much easier. Since the \(\log f(x)\) and \(f(x)\) are maximized at the same value of \(x\), the maximizer of the log likelihood function is also the maximizer of the likelihood function.

Example Let \(X_1, \ldots, X_n\) be a random sample from a Poisson distribution with mean \(\lambda\). Find the MLE of \(\lambda\).

We computed the likelihood function above as \[ L(x_1, \ldots, x_n) = e^{-n\lambda} \frac{\lambda^{\sum_{i = 1}^n x_i}}{\prod_{i = 1}^n x_i!} \] We take the log of both sides so that \[ \ln L(x_1, \ldots, x_n) = -n\lambda + \sum_{i = 1}^n x_i \ln \lambda - \ln(\prod_{i = 1}^n x_i!) \] We take the derivative with respect to \(\lambda\) to get \[ \frac {d}{d\lambda} \ln L(x_1, \ldots, x_n) = -n + \frac 1\lambda \sum_{i = 1}^n x_i. \] Set the derivative equal to zero and solve for \(\lambda\) to get our estimator \[ \hat \lambda = \frac 1n \sum_{i = 1}^n x_i. \] Note that this is indeed a maximum since the second derivative is everywhere negative.

The above example is typical of how to find MLE’s when the likelihood function is differentiable with respect to the parameter in question. When it is not, then we often can use common sense to find the maximum value as in the next example.

Example Let \(X_1, \ldots, X_n\) be a random sample from a uniform distribution on \([0, \theta]\). Find the maximum likelihood estimator of \(\theta\).

From above, we know that the likelihood function is \[ L(x_1, \ldots, x_n) = \frac {1}{\theta^n} I_{[0, \infty)}(x_{(1)}) I_{(-\infty, \theta]}(x_{(n)}) \] The piece \(I_{[0, \infty)}(x_{(1)})\) doesn’t depend on \(\theta\) and can be ignored, by assuming that all of the \(x_i\) are in the range \([0, \infty)\). The piece \(I_{(-\infty, \theta]}(x_{(n)})\) is one for any \(\theta\) such that \(x_{(n)} \le \theta\), but is zero for any \(\theta\) such that \(X_{(n)} < \theta\). Therefore, choosing \(\theta\) to yield a maximum requires that \(x_{(n)} \le \theta\). We are left with maximizing \(\frac {1}{\theta^n}\) over values of \(\theta\) that are bigger than or equal to \(x_{(n)}\). Since \(1/\theta^n\) is a decreasing function of \(\theta\), we want to make \(\theta\) as small as possible while still being greater than or equal to \(x_{(n)}\). That is, \(\hat \theta = x_{(n)}\).

15.9 Exercises

  1. Let \(X_1, \ldots, X_5\) be a random sample from a normal distribution with mean 0 and standard deviation 1. Show that \(X_1\) is an unbiased estimator for \(\mu\).

  2. Let \(X_1, \ldots, X_4\) be a random sample from a uniform distribution on \((-1, \theta)\), where \(\theta > -1\). Show that \(X_{(n)}\) (the maximum value of \(X_1, \ldots, X_4\)) is a biased estimator for \(\theta\), and suggest an unbiased estimator for \(\theta\) based on \(X_{(n)}\).

  3. Let \(X_1, \ldots, X_n\) be a random sample from a normal distribution with mean \(\mu\) and standard deviation \(\sigma\). Show that \(X_1\) is not a consistent estimator of \(\mu\). (Though, from problem 1, it is unbiased.)

  4. Use simulation to determine whether \(S\) seems to be a consistent estimator for \(\sigma\) when sampling from a normal distribution with \(\mu = 2\) and \(\sigma = 4\).
    1. Use \(\epsilon = 0.5\), and try \(N\) values of c(10, 20, 50, 100, 200, 500, 1000).
    2. Use \(\epsilon = 0.3\) and find a sequence of \(N\) values.
     

  5. Let \(X_1, \ldots, X_3\) be a random sample from a uniform distribution on \([0, 10]\). Show that the MSE of \(\frac 43 X_{(3)}\) is 6.666, and the MSE of \(\frac {3.6}{3} X_{(3)}\) is 6.4.

  6. Assume we have a random sample of size \(n\) from a normal distribution with mean 1 and standard deviation 2. 1.Show via simulation that \(\frac 1n \sum_{i = 1}^n (x_i - \overline{x})^2\) has a lower MSE when estimating \(\sigma^2\) than \(S^2\) does when \(n = 10\).

  7. Estimate the constant \(A\) such that \(\frac 1{n + A} \sum_{i = 1}^n (x_i - \overline{x})^2\) has minimum MSE for \(n = 10\).

  8. Let \(X_1, \ldots, X_n\) be a random sample from an exponential distribution with rate \(\lambda = 1\). We showed in the previous chapter that the sample median is a biased estimator for the median, \(\ln 2\). Determine via simulation whether the sample median appears to be asymptotically biased.

  1. One of the authors (DS) in his Masters oral exam made what he thought was a throw-away comment, that “everyone” uses \(S^2 = \frac 1{n-1}\sum (x_i - \overline{x})^2\) for the estimate of variance. One of his examiners did not.↩