Chapter 7 Inference on the Mean

Consider the brake data set, which comes from this paper. The data is available in the fosdata package. The authors noted that there have been several accidents involving unintended acceleration, where the driver was unable to realize that the car was accelerating in time to apply the brakes. This type of accident seems to happen more with older drivers, and the authors developed an experiment to test whether older drivers are less adept at correcting unintended acceleration.

The set-up of the experiment was as follows. Older (65+) drivers and younger (18-32) drivers were recruited for an experiment. The drivers were put in a simulation, and told to apply the brake when a light turned red. Ninety percent of the time, this would work as desired, but 10 percent of the time, the brake would instead speed up the car. The experimenters measured three things in the 10 percent case.

The length of time before the initial application of the brake.
The length of time before the brake was released.
The length of time before the pedal to the left of the brake was pressed, which would then stop the car.

The experimenters desire was to see whether there is a difference in the true mean times of participants in the different age groups to perform one of the three tasks.

You can get the data via

brake <- fosdata::brake

The authors collected a lot more data than we will be using in this chapter! Let’s look at boxplots of the latency (length of time) in stepping on the pedal after seeing the first red light. The time to step on the pedal after seeing a red light is latency_p1, the time between stepping on the brake and releasing it after realizing that the car is accelerating is latency_p2, and the time to step on the correct pedal after releasing the incorrect pedal is latency_p3.

select(brake, matches("latency_p[1-3]$|age_group")) %>%
  tidyr::pivot_longer(cols = starts_with("lat"), names_to = "type", values_to = "time") %>%
  ggplot(aes(x = type, y = time, color = age_group)) +
  geom_boxplot()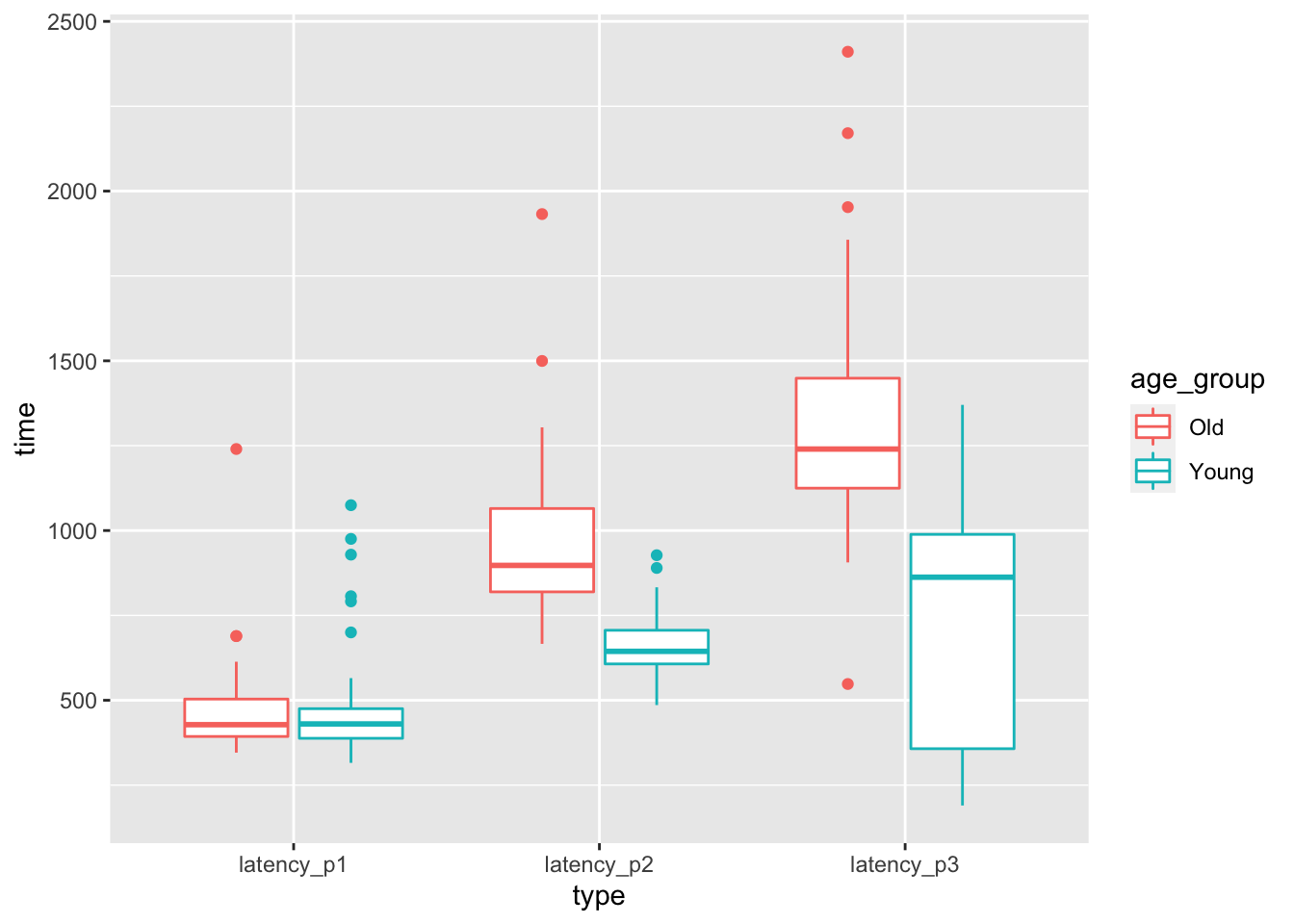

At a first glance, it seems like there may not be a difference in mean time to react to the red light between old and young, but there may well be a difference in the time to realize a mistake has been made. The purpose of this chapter is to be able to systematically study experiments such as this. For example, at the end of this chapter, we will be able to test whether the mean length of time for an older driver to release the pedal after it resulted in an unintended acceleration is the same as the mean length of time for a younger driver. We first develop some theory.

7.1 Notation and Theory

If $X_1,\ldots,X_n$ are iid normal rv’s with mean $\mu$ and standard deviation $\sigma$, then $\overline{X}$ is normal with mean $\mu$ and standard deviation $\sigma/\sqrt{n}$. It follows that \[ \frac{\overline{X} - \mu}{\sigma/\sqrt{n}} \sim Z \] where $Z$ is standard normal. One can use this information to do computations about probabilities of $\overline{X}$ in the case when $\sigma$ is known. However, many times, $\sigma$ is not known. In that case, we replace $\sigma$ by its estimate based on the data, $S$. The value $S/\sqrt{n}$ is called the standard error of $\overline{X}$. The standard error is no longer the standard deviation of $\overline{X}$, but an approximation that is also a random variable.

The question then becomes: what kind of distribution is \[ \frac{\overline{X} - \mu}{S/\sqrt{n}}? \]

Theorem 7.1 If $X_1,\ldots,X_n$ are iid normal rvs with mean $\mu$ and sd $\sigma$, then \[ \frac{\overline{X} - \mu}{S/\sqrt{n}} \] is $t$ with $n-1$ degrees of freedom.

We will not prove this theorem, but let’s verify through simulation that the pdf’s look similar in some special cases.

Example We simulate the pdf of $\frac{\overline{X} - \mu}{S/\sqrt{n}}$ when $n = 6$, $\mu = 3$ and $\sigma = 4$, and compare to the pdf of a $t$ rv with 3 degrees of freedom.

n <- 6
mu <- 3
sigma <- 4
tData <- replicate(10000, {
  normData <- rnorm(n, mu, sigma)
  (mean(normData) - mu) / (sd(normData) / sqrt(n))
})
f <- function(x) dt(x, n - 1)
ggplot(data.frame(tData), aes(x = tData)) +
  geom_density() +
  stat_function(fun = f, color = "red")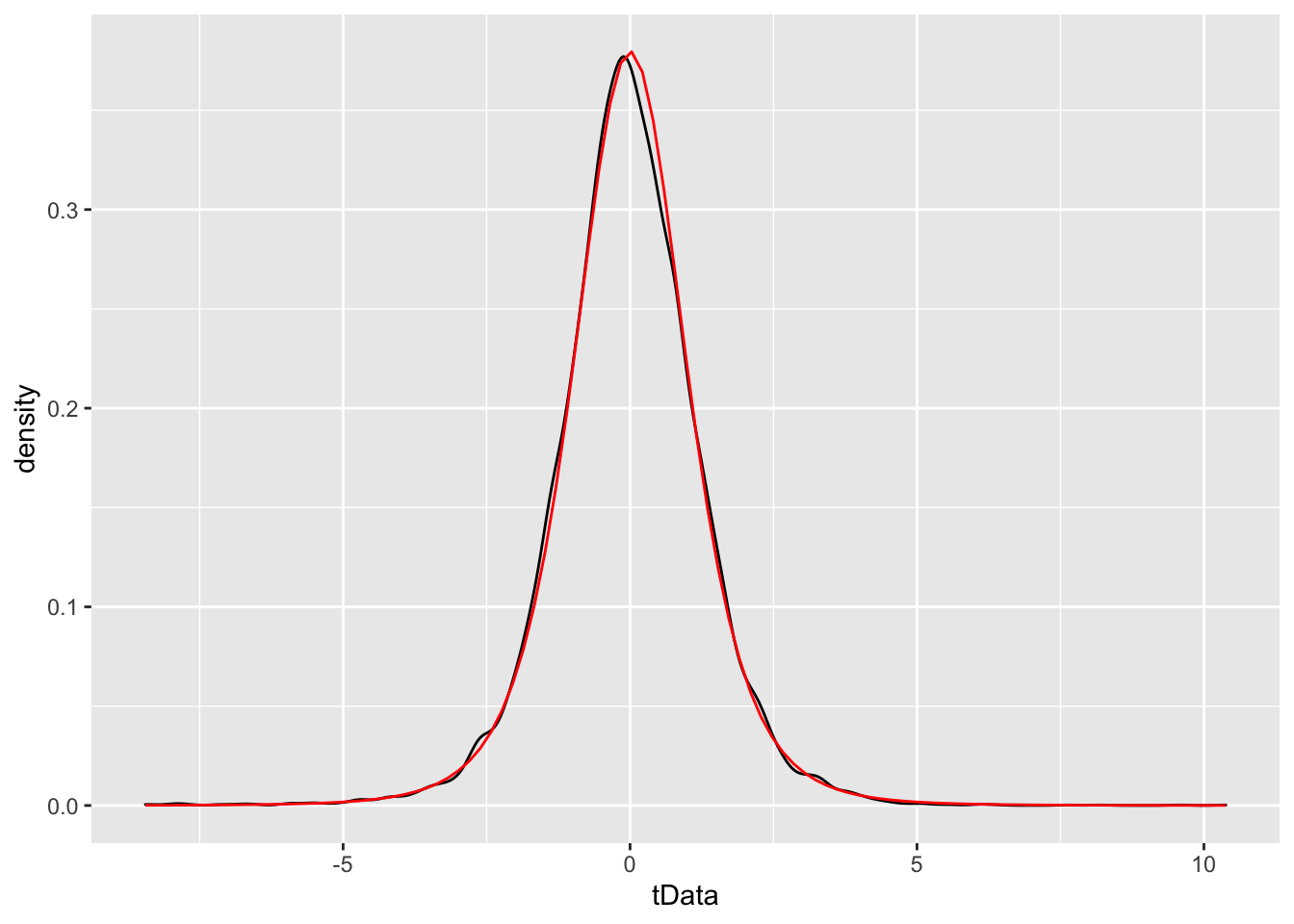

While certainly not a proof, the close match between the simulated values and the $t$-distribution is pretty convincing. Let’s compare to a standard normal random variable.

g <- function(x) dnorm(x)
ggplot(data.frame(tData), aes(x = tData)) +
  geom_density() +
  stat_function(fun = f, color = "red") +
  stat_function(fun = g, color = "green")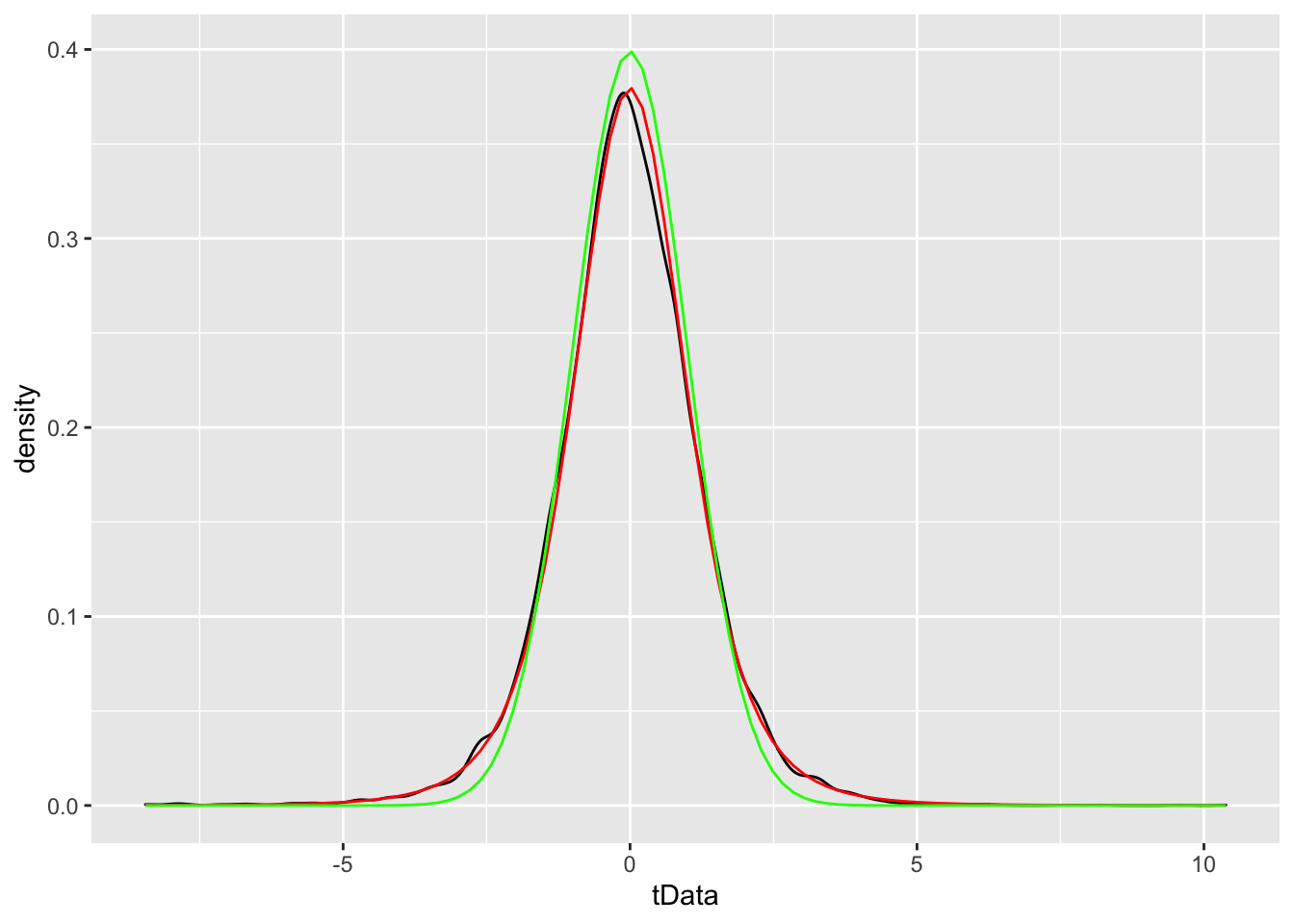

We see that the standard normal has lighter tails than the true distribution of $\frac{\overline{X} - \mu}{S/\sqrt{n}}$ does. Admittedly, the absolute difference in the two plots above is not spectacular, but in this section we will be interested precisely in estimating tail probabilities. If we compare

pt(-2.5, df = 3) - pnorm(-2.5)

## [1] 0.03764366

pt(-2.5, df = 3) / pnorm(-2.5)

## [1] 7.062107

we see that, while the absolute difference in areas is only 0.038, the area under the $t$ curve is about 7 times as large as the corresponding area under the standard normal curve, which is quite a difference. However, we do have the following theorem.

Theorem 7.2 For $n = 1, 2, \ldots$ let $X_n$ be a $t$ random variable with $n$ degrees of freedom. Let $Z$ be a standard normal random variable. Then, \[ \lim_{n \to \infty} X_n = Z \] in the sense that for every $a < b$, \[ \lim_{n \to \infty} P(a < X_n < b) = P(a < Z < b) \]

As an illustration, we plot the pdf’s of $t$ random variables with $n = 5$, $n = 20$ and $n = 50$ degrees of freedom versus a standard normal random variable.

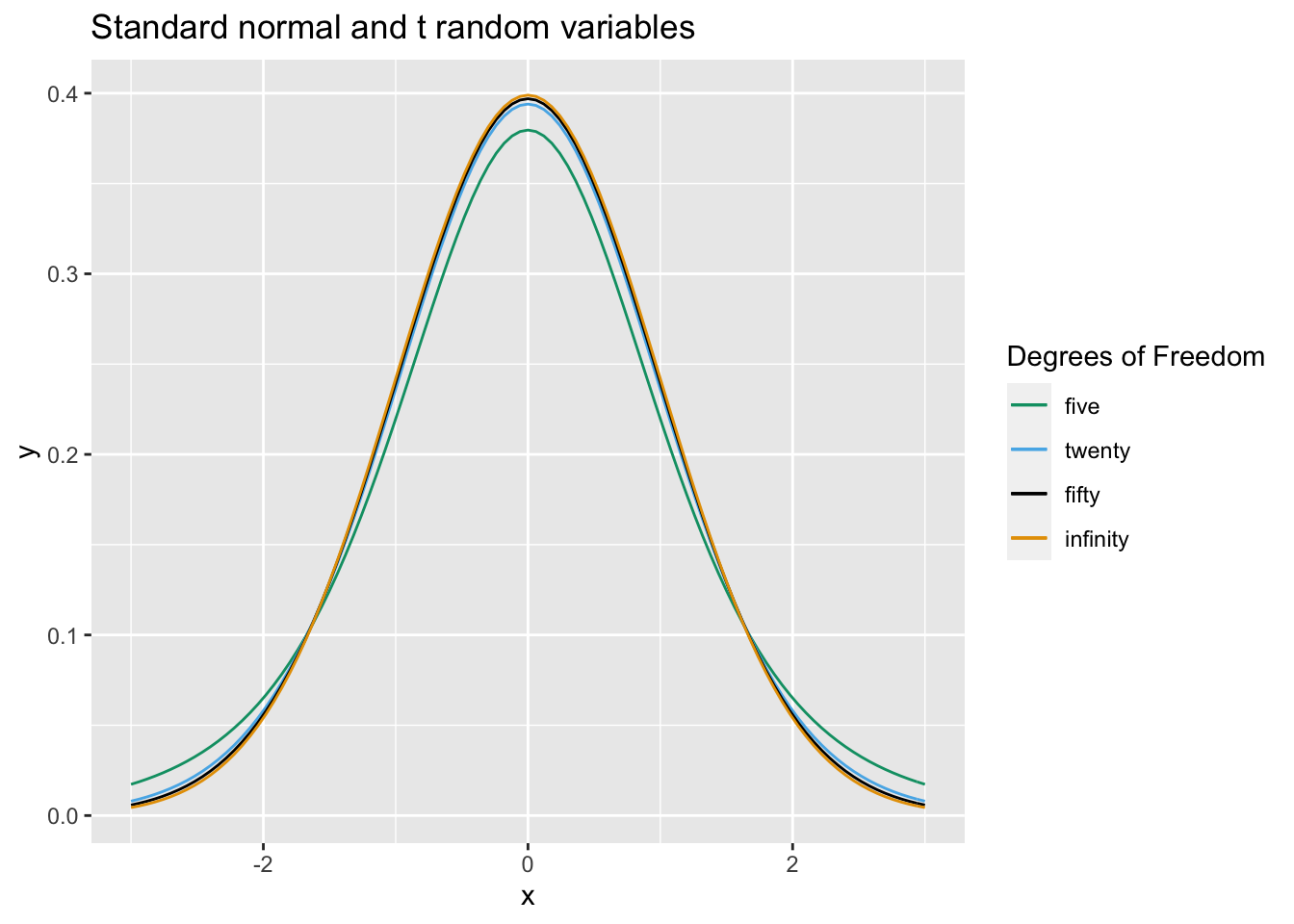
Exercise Simulate the pdf of $\frac{\overline{X} - \mu}{S/\sqrt{n}}$ when $n = 3$, $\mu = 5$ and $\sigma = 1$, and compare to the pdf of a $t$ random variable with 2 degrees of freedom.

Now, suppose that we don’t know either $\mu$ or $\sigma$, but we do know that our data is randomly sampled from a normal distribution. Let $t_{\alpha}$ be the unique real number such that $P(t > t_{\alpha}) = \alpha$, where $t$ has $n-1$ degrees of freedom. Note that $t_{\alpha}$ depends on $n$, because the $t$ distribution has more area in its tails when $n$ is small.

Then, we know that \[ P\left( t_{1 - \alpha/2} < \frac{\overline{X} - \mu}{S/\sqrt{n}} < t_{\alpha/2}\right) = 1 - \alpha. \]

By rearranging, we get

\[ P\left(\overline{X} + t_{1 - \alpha/2} S/\sqrt{n} < \mu < \overline{X} + t_{\alpha/2} S/\sqrt{n}\right) = 1 - \alpha. \]

Because the $t$ distribution is symmetric, $t_{1-\alpha/2} = -t_{\alpha/2}$, so we can rewrite the equation symmetrically as:

\[ P\left(\overline{X} - t_{\alpha/2} S/\sqrt{n} < \mu < \overline{X} + t_{\alpha/2} S/\sqrt{n}\right) = 1 - \alpha. \]

Let’s think about what this means. Take $n = 10$ and $\alpha = 0.10$ just to be specific. This means that if I were to repeatedly take 10 samples from a normal distribution with mean $\mu$ and any $\sigma$, then 90% of the time, $\mu$ would lie between $\overline{X} + t_{\alpha/2} S/\sqrt{n}$ and $\overline{X} - t_{\alpha/2} S/\sqrt{n}$. That sounds like something that we need to double check using a simulation!

t05 <- qt(.05, 9, lower.tail = FALSE)
mean(replicate(10000, {
  dat <- rnorm(10, 5, 8) # Choose mean 5 and sd 8
  xbar <- mean(dat)
  SE <- sd(dat) / sqrt(10)
  (xbar - t05 * SE < 5) & (xbar + t05 * SE > 5)
}))

The first line computes $t_{\alpha/2}$ using qt, the quantile function for the $t$ distribution, here with 9 DF. Then we check the inequality given above.

Think carefully about what value you expect to get here, then copy this code into R and run it. Were you right?

Exercise Repeat the above simulation with $n = 20$, $\mu = 7$ and $\alpha = .05$.

7.2 Confidence intervals for the mean

If we take a sample of size $n$ from iid normal random variables, then we call the interval

\[ \left[ \overline{X} - t_{\alpha/2} S/\sqrt{n},\ \ \overline{X} + t_{\alpha/2} S/\sqrt{n} \right] \] a 100(1 - $\alpha$)% confidence interval for $\mu$. As we saw in the simulation above, what this means is that if we repeat this experiment many times, then in the limit 100(1 - $\alpha$)% of the time, the mean $\mu$ will lie in the confidence interval.

Once we have done the experiment and we have an interval, it doesn’t make sense to talk about the probability that $\mu$ (a constant) is in the (constant) interval. There is nothing random there. There is also a more subtle issue with thinking of this as a probability. A procedure which will contain the true parameter value 95% of the time does not necessarily always create intervals that are about 95% “likely” (whatever meaning you attach to that) to contain the parameter value. Consider a procedure which is estimating the mean. It ignores the data and 95% of the time says that the mean is between $-\infty$ and $\infty$. The rest of the time it says the mean is exactly $\pi$. This procedure will contain the true parameter 95% of the time, but the intervals obtained are either 100% or 0% likely to contain the true mean, and when we see which interval we have, we know what the true likelihood is of it containing the mean. Nonetheless, it is widely accepted to say that we are 100(1 - $\alpha$)% confident that the mean is in the interval, which is what we will also do. When we say that we are 100(1 - $\alpha)$% confident that the mean is in the interval, we mean that if we repeated the procedure for generating the confidence interval over and over, then in the limit, the generated confidence interval would contain the mean 100(1 - $\alpha)$% of the time.

Our assumptions are

the population is normal, or that we have enough samples for the Central Limit Theorem to reasonably apply.
the sample is independent.

Before we continue, there are several ways that a sample can be dependent, and it is not normally possible to explicitly test whether the sample is independent. Here are a few things to look out for. First, if there is a time component to the data, you should be wary that the samples might depend on time. For example, if the data you are collecting is outdoor temperature, then the temperature observed very well could depend on time. Second, if you are repeating measurements, then the data is not independent. For example, if you have ratings of movies, then it is likely that each person has their own distribution of ratings that they give. So, if you have 10 ratings from each of 5 people, you would not expect the 50 samples to be independent. Third, if there is a change in the experimental setup, then you should not assume independence. We will see an example below where the experimenter changed the experiment after the 6th measurement. We can not assume that the measurements are independent of which setup was used.

To test normality of the population, we will examine histograms and boxplots of the data, calculate skewness, and run simulations to determine how large of a sample size is necessary for the Central Limit Theorem to make up for departures from normality.

As you might imagine, R has a built in command that creates confidence intervals for us. Consider the heart rate and body temperature data normtemp¹⁸.

You can read normtemp as follows.

normtemp <- fosdata::normtemp

What kind of data is this?

str(normtemp)

## 'data.frame':    130 obs. of  3 variables:
##  $ temp  : num  96.3 96.7 96.9 97 97.1 97.1 97.1 97.2 97.3 97.4 ...
##  $ gender: int  1 1 1 1 1 1 1 1 1 1 ...
##  $ bpm   : int  70 71 74 80 73 75 82 64 69 70 ...

head(normtemp)

##   temp gender bpm
## 1 96.3      1  70
## 2 96.7      1  71
## 3 96.9      1  74
## 4 97.0      1  80
## 5 97.1      1  73
## 6 97.1      1  75

We see that the data set is 130 observations of body temperature and heart rate. There is also gender information attached, that we will ignore for the purposes of this example.

Let’s visualize the data through a boxplot.

ggplot(normtemp, aes(x = " ", y = bpm)) +
  geom_boxplot(notch = TRUE)

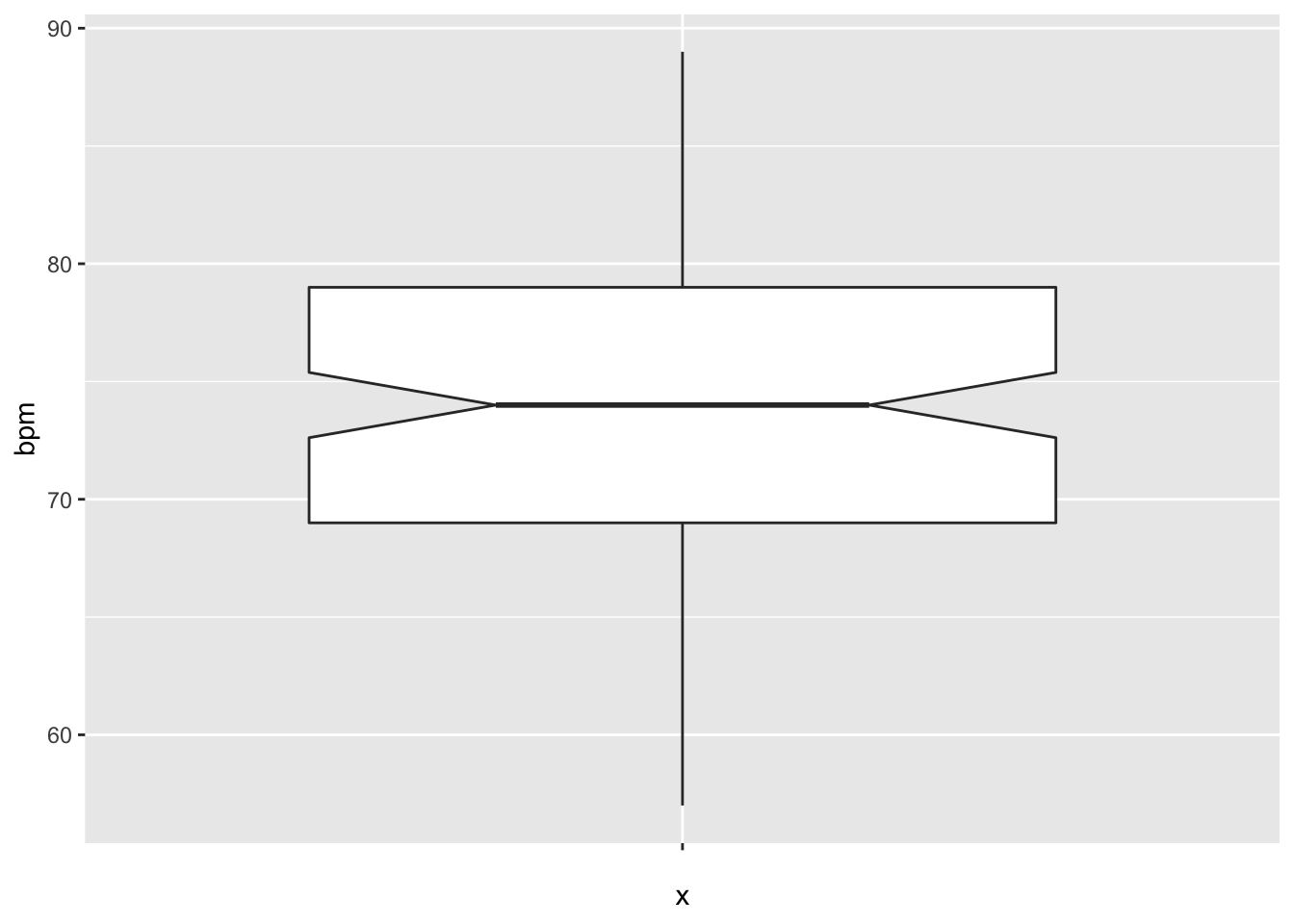
The data looks symmetric without outliers, and according to the plot, the true median should be about between 72 and 76.

Let’s find a 98% confidence interval for the mean heart rate of healthy adults. In order for this to be valid, we are assuming that we have a random sample from all healthy adults (highly unlikely to be formally true), and that the heart rate of healthy adults is normally distributed (also unlikely to be formally true). Later, we will discuss deviations from our assumptions and when we should be concerned.

The R command that finds a confidence interval for the mean in this way is

t.test(normtemp$bpm, conf.level = .98)

## 
##  One Sample t-test
## 
## data:  normtemp$bpm
## t = 119.09, df = 129, p-value < 2.2e-16
## alternative hypothesis: true mean is not equal to 0
## 98 percent confidence interval:
##  72.30251 75.22056
## sample estimates:
## mean of x 
##  73.76154

We get a lot of information, but we can pull out what we are looking for as the confidence interval [72.3, 75.2]. So, we are 98 percent confident that the mean heart rate of healthy adults is greater than 72.3 and less than 75.2. NOTE We are not saying anything about the mean heart rate of the people in the study. That is exactly 73.76154, and we don’t need to do anything fancy. We are making an inference about the mean heart rate of all healthy adults. Note that to be more precise, we might want to say it is the mean heart rate of all healthy adults as would be measured by this experimenter. Other experimenters could have a different technique for measuring heart rates which could lead to a different answer.

7.3 Hypothesis Tests of the Mean

In hypothesis testing, there is a null hypothesis and an alternative hypothesis. The null hypothesis can take on several forms: that a parameter is a specified value, that two population parameters are equal, that two population distributions are equal, and many others. The common thread being that it is a statement about the population distribution. Typically, the null hypothesis is the default assumption, or the conventional wisdom about a population. Often it is exactly the thing that a researcher is trying to show is false. The alternative hypothesis states that the null hypothesis is false, sometimes in a particular way.

Consider as an example, the body temperature of healthy adults, as in the previous subsection. The natural choice for the null and alternative hypothesis is

$H_0: \, \mu = 98.6$ versus

$H_a: \, \mu \not= 98.6$.

We will either reject $H_0$ in favor of $H_a$, or we will not reject $H_0$ in favor of $H_a$. (Note that this is different than accepting $H_0$.) There are two types of errors that can be made: Type I is when you reject $H_0$ when $H_0$ is actually true, and Type II is when you fail to reject $H_0$ when $H_a$ is actually true. For now, we will worry about controlling the probability of a Type I error.

In order to compute the probability of a type I error, we imagine that we collect the same type of data many times, when $H_0$ is actually true. We decide that we will reject $H_0$ if the data is sufficiently unlikely given that the null hypothesis is true. Formally, we will summarize the data into a single test statistic, and we will reject $H_0$ if the test statistics falls in a rejection region consisting of unlikely events under $H_0$. The probability of a type I error is then the probability that the data falls in the rejection region given that $H_0$ is true.

Returning to the specifics of $H_0: \mu = \mu_0$ versus $H_a: \mu \not= \mu_0$, we compute the test statistic \[ T = \frac{\overline{X} - \mu}{S/\sqrt{n}} \] And we ask: if I decide to reject $H_0$ based on this test statistic, what percentage of the time would I get data at least that much against $H_0$ given that $H_0$ is true? In other words, if I decide to reject $H_0$ based on $T$, I would have to reject $H_0$ for any data that is even more compelling against $H_0$. How often would that happen under $H_0$? Well, that is what the $p$-value is.

We can compute the $p$-value using R in multiple ways. First, we recall that under the assumption that the underlying population is normal, $T$ has a $t$ distribution with 129 degrees of freedom. The test statistic in our case is

(mean(normtemp$temp) - 98.6) / (sd(normtemp$temp) / sqrt(130))

## [1] -5.454823

We also note that values more negative than $-5.45$ would be more compelling evidence against $H_0$, as would values that are at least $5.45$. The probability that $T$ falls in the interval $(-\infty, -5.45] \cup [5.45, \infty)$ is given by

t_stat <- (mean(normtemp$temp) - 98.6) / (sd(normtemp$temp) / sqrt(130))
pt(t_stat, df = 129) + pt(-t_stat, df = 129, lower.tail = F)

## [1] 2.410632e-07

As one would expect, R also has automated this procedure in the function t.test. In this case, one would use

t.test(normtemp$temp, mu = 98.6)

## 
##  One Sample t-test
## 
## data:  normtemp$temp
## t = -5.4548, df = 129, p-value = 2.411e-07
## alternative hypothesis: true mean is not equal to 98.6
## 95 percent confidence interval:
##  98.12200 98.37646
## sample estimates:
## mean of x 
##  98.24923

Either way, we get a $p$-value of about 0.000002, which is the probability of obtaining data at least this compelling against $H_0$ when $H_0$ is true. In other words, it is very unlikely that this data would be collected if the true mean temp of healthy adults is 98.6. (Again, we are assuming a random sample of healthy adults and normal distribution of temperatures of healthy adults.)

Example Let’s consider the Cavendish data set in the HistData package. Henry Cavendish carried out experiments in 1798 to determine the mean density of the earth. He collected 29 measurements, but changed the exact set-up of his experiment after the 6th measurement.

The current accepted value for the mean density of the earth is $5.515 kg/m^3$. Let’s examine Cavendish’s data from that modern perspective and test $H_0: \mu = 5.515$ versus $H_a: \mu\not= 5.515$. The null hypothesis is that Cavendish’s experimental measurements were unbiased, and that the true mean was the correct value. The alternative is that his set-up had some inherent bias.

A first question that comes up is: what are we going to do with the first six observations? Since the experimental setup was changed after the 6th measurement, it seems likely that the first six observations are not independent of the rest of the observations. Hence, we will proceed by throwing out the first six observations. The variable density3 contains the measurements with the first 6 values removed.

Let’s look at a boxplot of the data.

cavendish <- HistData::Cavendish
ggplot(cavendish, aes(x = "", y = density3)) +
  geom_boxplot(outlier.size = -1) +
  geom_jitter(height = 0, width = 0.2)

## Warning: Removed 6 rows containing non-finite values (stat_boxplot).

## Warning: Removed 6 rows containing missing values (geom_point).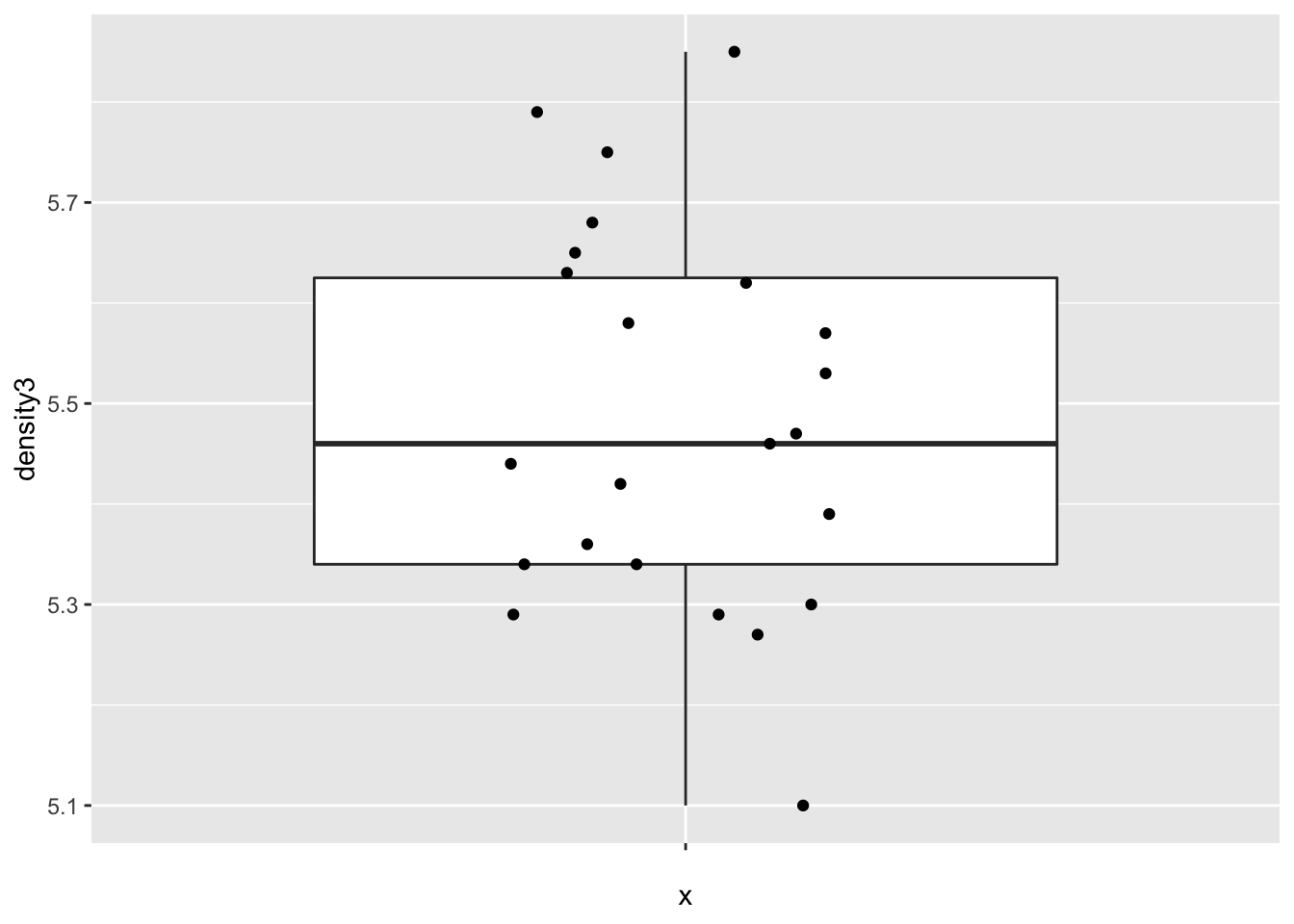

The data appears plausibly to be from a normal distribution, and there are no significant outliers.

t.test(cavendish$density3, mu = 5.5155)

## 
##  One Sample t-test
## 
## data:  cavendish$density3
## t = -0.80648, df = 22, p-value = 0.4286
## alternative hypothesis: true mean is not equal to 5.5155
## 95 percent confidence interval:
##  5.401134 5.565822
## sample estimates:
## mean of x 
##  5.483478

We get a 95 percent confidence interval of $[5.40, 5.57]$, which does contain the current accepted value of 5.5155. We also obtain a $p$-value of .4286, so we would not reject $H_0: \mu = 5.5155$ at the $\alpha = .05$ level. We conclude that there is not evidence that the mean value of Cavendish’s experiment differed from the currently accepted value.

7.4 One-sided Confidence Intervals and Hypothesis Tests

Consider the cows_small data set from the fosdata . This data set can be loaded as follows. If you are interested in the full, much more complicated data set, that can be found in fosdata::cows.

cows <- fosdata::cows_small

On hot summer days, cows in Davis, CA were sprayed with water for three minutes and the change in temperature as measured at the shoulder was measured. There are three different treatments of cows, including the control, which we ignore in this example (we will come back to that later in the class). For now, we are only interested in the nozzle type tk_0_75. In this case, we have reason to believe before the experiment begins that spraying the cows with water will lower their temperature. So, we are not as much interested in detecting a change in temperature, but a decrease in temperature. Additionally, should it turn out by some oddity that spraying the cows with water increased their temperature, we would not act on that information; we will only make a recommendation of using nozzle tk_0_75 if it decreases the temperature of the cows. This changes our analysis.

Before proceeding, let’s look at some plots of the data.

ggplot(cows, aes(x = tk_0_75)) +
  geom_histogram(bins = 6)

ggplot(cows, aes(x = "", y = tk_0_75)) +
  geom_boxplot(outlier.size = -1) +
  geom_jitter(hight = 0, width = 0.2)

## Warning: Ignoring unknown parameters: hight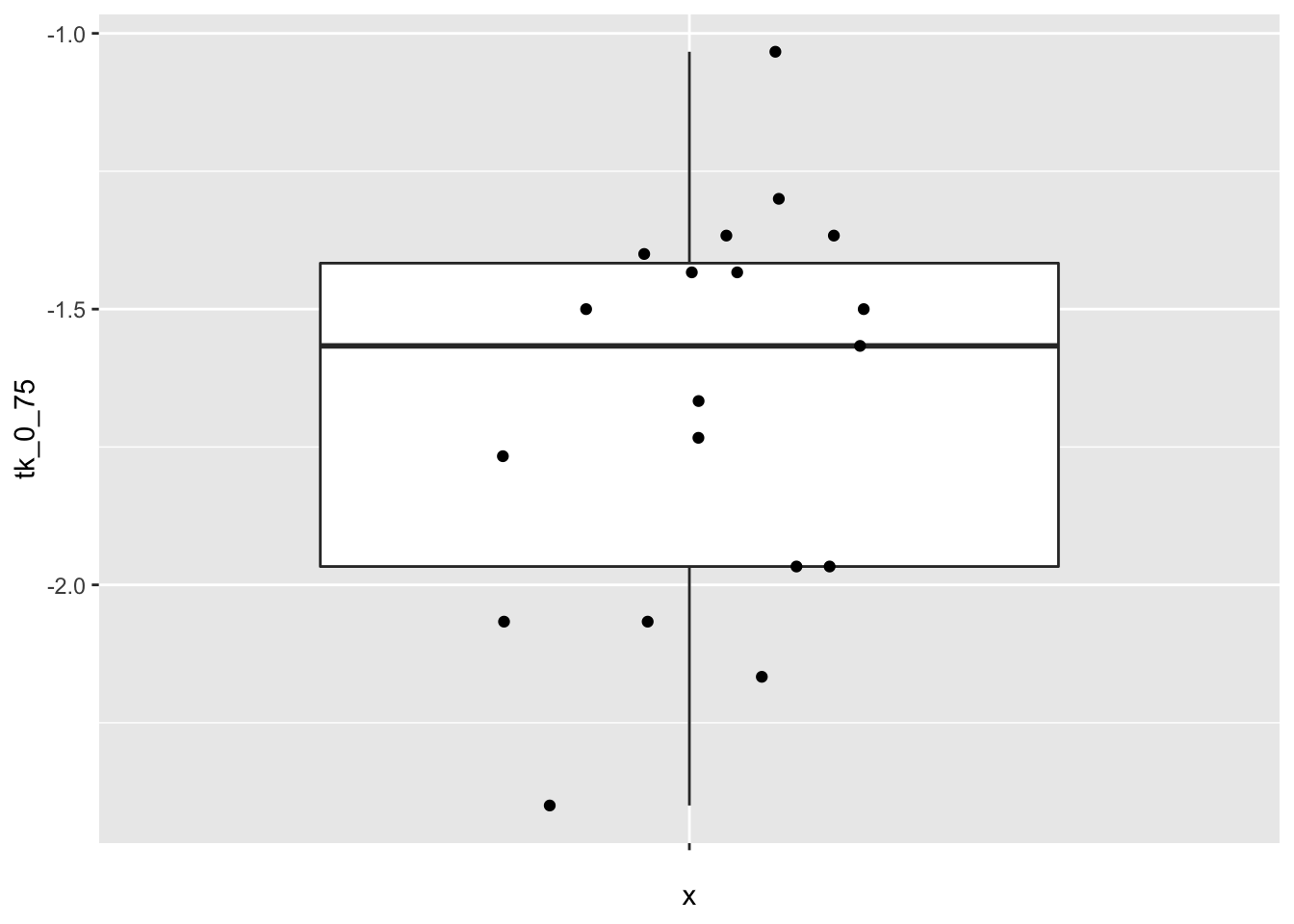

The data seems to plausibly come from a normal distribution, there don’t seem to be any outliers, and independence is not in question.

We will construct a 98% confidence interval for the change in temperature of the form $(-\infty, R)$. We will say that we are 98% confident that the treatment results in a temperature change of at most $R$ degrees Celsius. As before, this interval will be constructed so that 98% of the time that we perform the experiment, the true mean will fall in the interval (and 2% of the time, it will not). As before, we are assuming normality of and independent samples from the underlying population. We will also perform the following hypothesis test:

$H_0: \mu \ge 0$ vs

$H_a: \mu < 0$

There is no difference in how we would run the test between $H_0: \mu \ge 0$ and $H_0: \mu = 0$ in this case, but knowing the alternative is $\mu < 0$ makes a difference. Now, the evidence that is least likely under $H_0$ (and most in favor of $H_a$) is all of the form $\overline{x} < R$. So, the percent of time we would make a type I error under $H_0$ is \[ P(\frac{\overline{X} - \mu_0}{S/\sqrt{n}} < R) \] where $\mu_0 = 0$ in this case. After collecting data, if we reject $H_0$, we would also have rejected $H_0$ if we got more compelling evidence against $H_0$, so we would compute \[ P(t_{n-1} > \frac{\overline{x} - \mu_0}{S/\sqrt{n}}) \] where $\frac{\overline{x} - \mu_0}{S/\sqrt{n}}$ is the value computed from the data. R does all of this for us:

t.test(cows$tk_0_75, mu = 0, alternative = "less", conf.level = .98)

## 
##  One Sample t-test
## 
## data:  cows$tk_0_75
## t = -20.509, df = 18, p-value = 3.119e-14
## alternative hypothesis: true mean is less than 0
## 98 percent confidence interval:
##       -Inf -1.488337
## sample estimates:
## mean of x 
## -1.668421

The confidence interval for the change in temperature associated with nozzle TK-0.75 is $(-\infty, -1.49)$ degrees Celsius. That is, we are 98 percent confident that the mean drop in temperature is at least 1.49 degrees Celsius. The $p$-value associated with the hypothesis test is $p = 3.1 \times 10^{-14}$, so we would reject $H_0$ that the mean temperature change is zero. We conclude that use of nozzle TK-0.75 is associated with a mean drop in temperature after three minutes as measured at the shoulder of the cows.

7.5 Simulations

In the chapter up to this point, we have assumed that the underlying data is a random sample from a normal distribution. Let’s look at how various types of departures from that assumption affect the validity of our statistical procedures. For the purposes of this discussion, we will restrict to hypothesis testing at a specified $\alpha$ level, but our results will hold for confidence intervals and reporting $p$-values just as well.

Our point of view is that if we design our hypothesis test at the $\alpha = .1$ level, say, then we want to incorrectly reject the null hypothesis 10% of the time. That is how our test is designed. If our assumptions of normality are violated, then we want to measure the new effective type I error rate and compare it to 10%. If the new error rate is far from 10%, then the test is not performing as designed. We will note whether the test makes too many type I errors or too few, but the main objective is to see whether the test is performing as designed.

Our first observation is that when the sample size is large, then the central limit theorem tells us that $\overline{X}$ is approximately normal. Since $t_n$ is also approximately normal when $n$ is large, this gives us some measure of protection against departures from normality in the underlying population. It will be very useful to pull out the $p$-value of the t.test. Let’s see how we can do that. We begin by doing a t.test on “garbage data” just to see what t.test returns.

str(t.test(c(1, 2, 3)))

## List of 10
##  $ statistic  : Named num 3.46
##   ..- attr(*, "names")= chr "t"
##  $ parameter  : Named num 2
##   ..- attr(*, "names")= chr "df"
##  $ p.value    : num 0.0742
##  $ conf.int   : num [1:2] -0.484 4.484
##   ..- attr(*, "conf.level")= num 0.95
##  $ estimate   : Named num 2
##   ..- attr(*, "names")= chr "mean of x"
##  $ null.value : Named num 0
##   ..- attr(*, "names")= chr "mean"
##  $ stderr     : num 0.577
##  $ alternative: chr "two.sided"
##  $ method     : chr "One Sample t-test"
##  $ data.name  : chr "c(1, 2, 3)"
##  - attr(*, "class")= chr "htest"

It’s a list of 9 things, and we can pull out the $p$-value by using t.test(c(1,2,3))$p.value.

7.5.1 Symmetric, light tailed

Example Estimate the effective type I error rate in a t-test of $H_0: \mu = 0$ versus $H_a: \mu\not = 0$ at the $\alpha = 0.1$ level when the underlying population is uniform on the interval $(-1,1)$ when we take a sample size of $n = 10$.

Note that $H_0$ is definitely true in this case. So, we are going to estimate the probability of rejecting $H_0$ under the scenario above, and compare it to 10%, which is what the test is designed to give. Let’s build up our replicate function step by step.

set.seed(1)
runif(10, -1, 1) # Sample of size 10 from uniform rv

##  [1] -0.4689827 -0.2557522  0.1457067  0.8164156 -0.5966361  0.7967794
##  [7]  0.8893505  0.3215956  0.2582281 -0.8764275

t.test(runif(10, -1, 1))$p.value # p-value of test

## [1] 0.5089686

t.test(runif(10, -1, 1))$p.value < .1 # true if we reject

## [1] FALSE

mean(replicate(10000, t.test(runif(10, -1, 1))$p.value < .1))

## [1] 0.1007

Our result is 10.07%. That is really close to the designed value of 10%.

Exercise Repeat the above example for various values of $\alpha$ and $n$. How big does $n$ need to be for the t.test to give results close to how it was designed? (Note: there is no one right answer to this ill-posed question! There are, however, wrong answers. The important part is the process you use to investigate.)

7.5.2 Skew

Example Estimate the effective type I error rate in a t-test of $H_0: \mu = 1$ versus $H_a: \mu\not = 1$ at the $\alpha = 0.05$ level when the underlying population is exponential with rate 1 when we take a sample of size $n = 20$.

set.seed(2)
mean(replicate(20000, t.test(rexp(20, 1), mu = 1)$p.value < .05))

## [1] 0.08305

Note that we have to specify the null hypothesis mu = 1 in the t.test. Here we get an effective type I error rate (rejecting $H_0$ when $H_0$ is true) that is 3.035 percentage points higher than designed. This means our error rate will increase by 61%. Most people would argue that the test is not working as designed.

One issue is the following: how do we know we have run replicate enough times to get a reasonable estimate for the probability of a type I error? Well, we don’t. If we repeat our experiment a couple of times, though, we see that we get consistent results, which for now we will take as sufficient evidence that our estimate is closer to correct.

mean(replicate(20000, t.test(rexp(20, 1), mu = 1)$p.value < .05))

## [1] 0.08135

mean(replicate(20000, t.test(rexp(20, 1), mu = 1)$p.value < .05))

## [1] 0.0836

Pretty similar each time. That’s reason enough for me to believe the true type I error rate is relatively close to what we computed.

We summarize the simulated effective Type I error rates for $H_0: \mu = 1$ versus $H_a: \mu \not= 1$ at $\alpha = .1, .05, .01$ and $.001$ levels for sample sizes $N = 10, 20, 50, 100$ and 200.

effectiveError <- sapply(c(.1, .05, .01, .001), function(y) {
  sapply(c(10, 20, 50, 100, 200), function(x) {
    mean(replicate(20000, t.test(rexp(x, 1), mu = 1)$p.value < y))
    })
  })
colnames(effectiveError) <- c(".1", ".05", ".01", ".001")
rownames(effectiveError) <- c("10", "20", "50", "100", "200")
as_tibble(effectiveError)

## # A tibble: 5 x 4
##    `.1`  `.05`  `.01`  `.001`
##   <dbl>  <dbl>  <dbl>   <dbl>
## 1 0.144 0.0962 0.047  0.0144 
## 2 0.130 0.0826 0.0327 0.0120 
## 3 0.112 0.0673 0.0216 0.00745
## 4 0.109 0.0588 0.0180 0.0045 
## 5 0.105 0.0545 0.0140 0.00255

Exercise Repeat the above example for exponential rv’s when you have a sample size of 150 for $\alpha = .1$, $\alpha = .01$ and $\alpha = .001$. I recommend increasing the number of times you are replicating as $\alpha$ gets smaller. Don’t go crazy though, because this can take a while to run.

From the previous exercise, you should be able to see that at $n = 50$, the effective type I error rate gets worse in relative terms as $\alpha$ gets smaller. (For example, my estimate at the $\alpha = .001$ level is an effective error rate more than 6 times what is designed! We would all agree that the test is not performing as designed.) That is unfortunate, because small $\alpha$ are exactly what we are interested in! That’s not to say that t-tests are useless in this context, but $p$-values should be interpreted with some level of caution when there is thought that the underlying population might be exponential. In particular, it would be misleading to report a $p$-value with 7 significant digits in this case, as R does by default, when in fact it is only the order of magnitude that is significant. Of course, if you know your underlying population is exponential before you start, then there are techniques that you can use to get accurate results which are beyond the scope of this textbook.

7.5.3 Heavy tails and outliers

If the results of the preceding section didn’t convince you that you need to understand your underlying population before applying a t-test, then this section will. A typical “heavy tail” distribution is the $t$ random variable. Indeed, the $t$ rv with 1 or 2 degrees of freedom doesn’t even have a finite standard deviation!

Example Estimate the effective type I error rate in a t-test of $H_0: \mu = 0$ versus $H_a: \mu\not = 0$ at the $\alpha = 0.1$ level when the underlying population is $t$ with 3 degrees of freedom when we take a sample of size $n = 30$.

mean(replicate(20000, t.test(rt(30, 3), mu = 0)$p.value < .1))

## [1] 0.09735

Not too bad. It seems that the t-test has an effective error rate less than how the test was designed.

Example Estimate the effective type I error rate in a t-test of $H_0: \mu = 3$ versus $H_a: \mu\not = 3$ at the $\alpha = 0.1$ level when the underlying population is normal with mean 3 and standard deviation 1 with sample size $n = 100$. Assume, however, that there is an error in measurement, and one of the values is multiplied by 100 due to a missing decimal point.

mean(replicate(20000, {
  dat <- c(rnorm(99, 3, 1), 100 * rnorm(1, 3, 1))
  t.test(dat, mu = 3)$p.value < .1
}))

## [1] 3e-04

These numbers are so small, it makes more sense to sum them:

sum(replicate(20000, {
  dat <- c(rnorm(99, 3, 1), 100 * rnorm(1, 3, 1))
  t.test(dat, mu = 3)$p.value < .1
}))

## [1] 6

So, in this example, you see that we would reject $H_0$ 6 out of 20,000 times, when the test is designed to reject it 2,000 times out of 20,000! You might as well not even bother running this test, as you are rarely, if ever, going to reject $H_0$ even when it is false.

Example Estimate the percentage of time you would correctly reject $H_0: \mu = 7$ versus $H_a: \mu\not = 7$ at the $\alpha = 0.1$ level when the underlying population is normal with mean 3 and standard deviation 1 with sample size $n = 100$. Assume, however, that there is an error in measurement, and one of the values is multiplied by 100 due to a missing decimal point.

Note that here, we have a null hypothesis that is 4 standard deviations away from the true null hypothesis. That should be easy to spot. Let’s see.

mean(replicate(20000, t.test(c(rnorm(99, 3, 1), 100 * rnorm(1, 3, 1)), mu = 7)$p.value < .1))

## [1] 0.07285

There is no “right” value to compare this number to. We have estimated the probability of correctly rejecting a null hypothesis that is 4 standard deviations away from the true value (which is huge!!) as 0.0722. So, we would only detect a difference that large about 7% of the time that we run the test. That’s hardly worth doing.

7.5.4 Summary

When doing t-tests on populations that are not normal, the following types of departures from design were noted.

When the underlying distribution is skew, the exact $p$-values should not be reported to many significant digits (especially the smaller they get). If a $p$-value close to the $\alpha$ level of a test is obtained, then we would want to note the fact that we are unsure of our $p$-values due to skewness, and fail to reject.
When the underlying distribution has outliers, the power of the test is severely compromised. A single outlier of sufficient magnitude will force a t-test to never reject the null hypothesis. If your population has outliers, you do not want to use a t-test.

7.6 Two sample hypothesis tests of $\mu_1 = \mu_2$

Here, we present a couple of examples of two sample t tests. In this situation, we have two populations that we are sampling from, and we are wondering whether the mean of population one differs from the mean of population two. At least, that is the problem we are typically working on!

The assumptions for t tests remain the same. We are assuming that the underlying populations are normal, or that we have enough samples so that the central limit theorem takes hold. We are also AS ALWAYS assuming that there are no outliers. Remember: outliers can kill t tests. Both the one-sample and the two-sample variety.

We also have two other choices.

We can assume that the variances of the two populations are equal. If the variances of the two populations really are equal, then this is the correct thing to do. In general, it is a more conservative approach not to assume the variances of the two populations are equal, and I generally recommend not to assume equal variance unless you have a good reason for doing so.
Whether the data is paired or unpaired. Paired data results from multiple measurements of the same individual at different times, while unpaired data results from measurements of different individuals. Say, for example, you wish to determine whether a new fertilizer increases the mean number of apples that apple trees produce. If you count the number of apples one season, and then the next season apply the fertilizer and count the number of apples again, then you would expect there to be some relationship between the number of apples you count in each season (big trees would have more apples each season than small trees, for example). If you randomly selected half of the trees to apply fertilizer to in one growing season, then there would not be any dependencies in the data.In general, it is a hard problem to deal with dependent data, but paired data is one type of data that we can deal with.

Example We return to the brake data in the fosdata package. Recall that we were interested in whether there is a difference in the mean time for an older person and the mean time for a younger person to release the brake pedal after it unexpectedly causes the car to speed up.

Let $\mu_1$ be the mean time to release the pedal for the older group, and let $\mu_2$ denote the mean time of the younger group in ms.

\[ H_0: \mu_1 = \mu_2 \] versus \[ H_a: \mu_1\not= \mu_2 \]

It might be reasonable to do a one-sided test here if you have data or other evidence suggesting that older drivers are going to have slower reaction times, but we will stick with the two-sided tests.

Let’s think about the data that we have for a minute. Do we expect the reaction times to be approximately normal? How many samples do we have?

brake <- fosdata::brake

We have 80 observations. Let’s compute the mean, sd, skewness and number of observations in each group.

brake %>%
  group_by(age_group) %>%
  summarize(
    mean = mean(latency_p2),
    sd = sd(latency_p2),
    skew = e1071::skewness(latency_p2),
    N = n()
  )

## `summarise()` ungrouping output (override with `.groups` argument)

## # A tibble: 2 x 5
##   age_group  mean    sd  skew     N
##   <chr>     <dbl> <dbl> <dbl> <int>
## 1 Old        956. 242.  1.89     40
## 2 Young      664.  95.9 0.780    40

We see that the older group in particular is right skew. Let’s look at some plots.

ggplot(brake, aes(x = age_group, y = latency_p2)) +
  geom_boxplot(outlier.size = -1) +
  geom_jitter(height = 0, width = .2)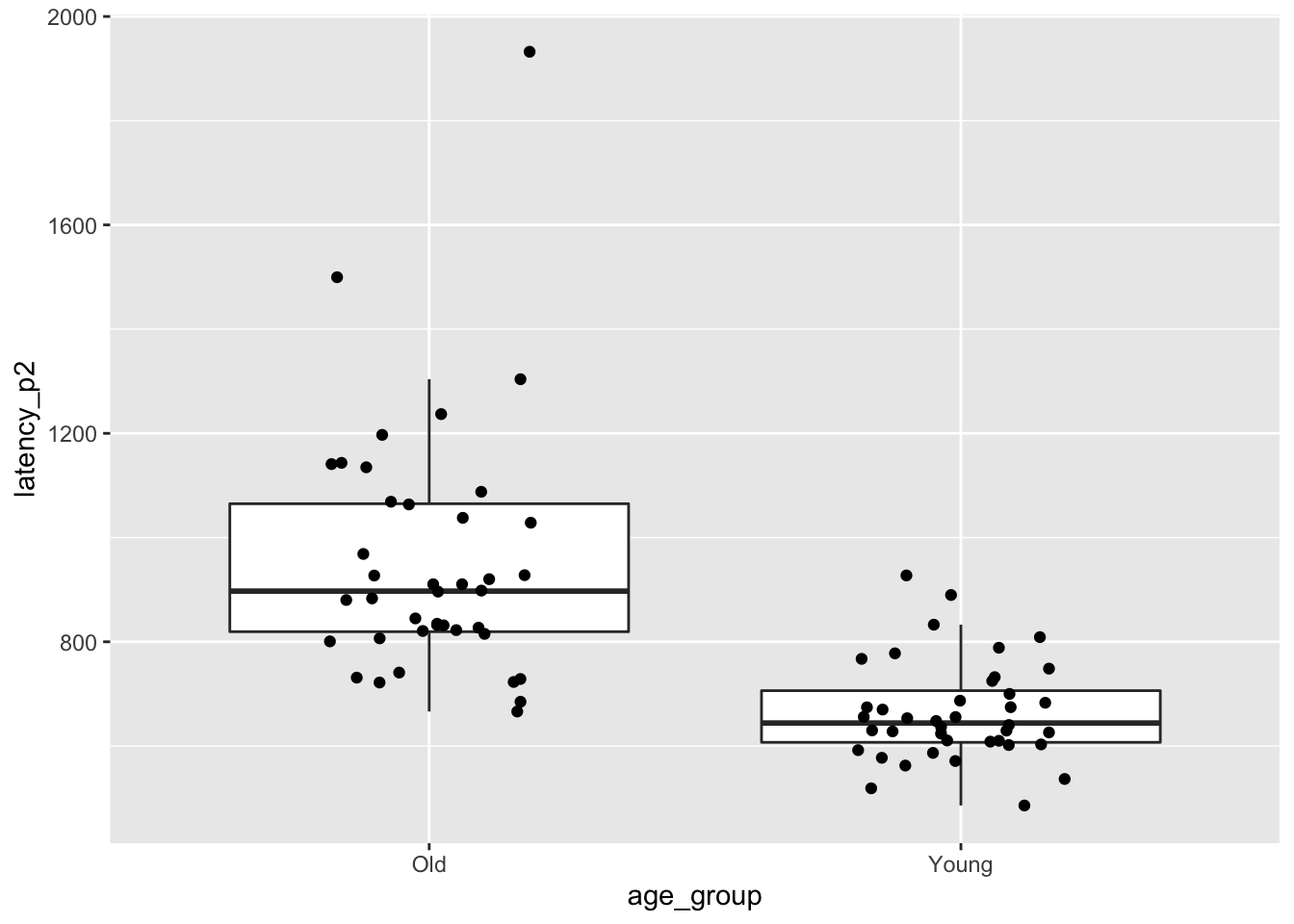

We see that there is one relatively extreme outlier in the older drivers group. We will run the analysis two times, both with and without the outlier to see whether it is making a difference. Since our data is in long format, it is easier to use the formula version of t.test. In this case, we are telling t.test to break up latency_p2 by age_group and perform a two-sample t-test.

t.test(latency_p2 ~ age_group, data = brake)

## 
##  Welch Two Sample t-test
## 
## data:  latency_p2 by age_group
## t = 7.0845, df = 50.97, p-value = 4.014e-09
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  208.7430 373.8345
## sample estimates:
##   mean in group Old mean in group Young 
##            955.7747            664.4859

We would reject the null hypothesis that the two means are the same ($p = 4.0 \times 10^{-9}$). A 95 percent confidence interval for the difference in mean times is $[209, 374]$ ms. That is, we are 95 percent confident that the mean time for older drivers is between 209 and 374 ms slower than the mean time for younger drivers.

In exercise @(brakeoutlier), you are asked to redo the above analysis after removing the largest older driver outlier. When doing so, you will see that the skewness is improved, the $p$-value gets smaller, and the confidence interval gets more narrow. Therefore, we have no reason to doubt the validity of the work we did with the outlier included.

Example Returning to the cows_small data set in the fosdata package, we wish to determine whether there is a difference between nozzle TK-0.75 and nozzle TK-12 in terms of the mean amount that they cool down cows in a three minute period.

Let $\mu_1$ denote the mean change in temperature of cows sprayed with TK-0.75 and let $\mu_2$ denote the mean change in temperature of cows sprayed with TK-12. According to the manufacturer of the TK-0.75, it sprays 0.4 liters per minute at 40 PSI, while the TK-12 sprays 4.5 liters per minute. Our null hypothesis is $H_0: \mu_1 = \mu_2$ and our alternative is $H_a: \mu_1\not= \mu_2$. Since the TK-12 sprays considerably more water, it would be worth at least considering whether to do a one-sided test in this case. However, since we don’t know any other characteristics of the nozzles, which might mitigate the flow advantage of the TK-12, we stick with a two-sided test.

We begin by creating some summary statistics after pivoting to a long format.

cows_small <- fosdata::cows_small
cows_small %>%
  tidyr::pivot_longer(cols = -cow, names_to = "nozzle", values_to = "temp_change") %>%
  filter(nozzle != "control") %>%
  group_by(nozzle) %>%
  summarize(
    mean = mean(temp_change),
    sd = sd(temp_change),
    skew = e1071::skewness(temp_change),
    N = n()
  )

## `summarise()` ungrouping output (override with `.groups` argument)

## # A tibble: 2 x 5
##   nozzle   mean    sd   skew     N
##   <chr>   <dbl> <dbl>  <dbl> <int>
## 1 tk_0_75 -1.67 0.355 -0.329    19
## 2 tk_12   -1.80 0.323 -0.562    19

This looks pretty good. Both measures of temperature change are mildly left-skew, so normality does not seem to be an issue. However, independence does seem to be a possible issue. Since the same cows are used with both nozzles, it is likely that the temperature changes are related to one another and not independent. Therefore, we will use a paired t-test.

Let’s visualize the differences of the temperature changes.

ggplot(cows_small, aes(y = tk_12 - tk_0_75)) +
  geom_boxplot()

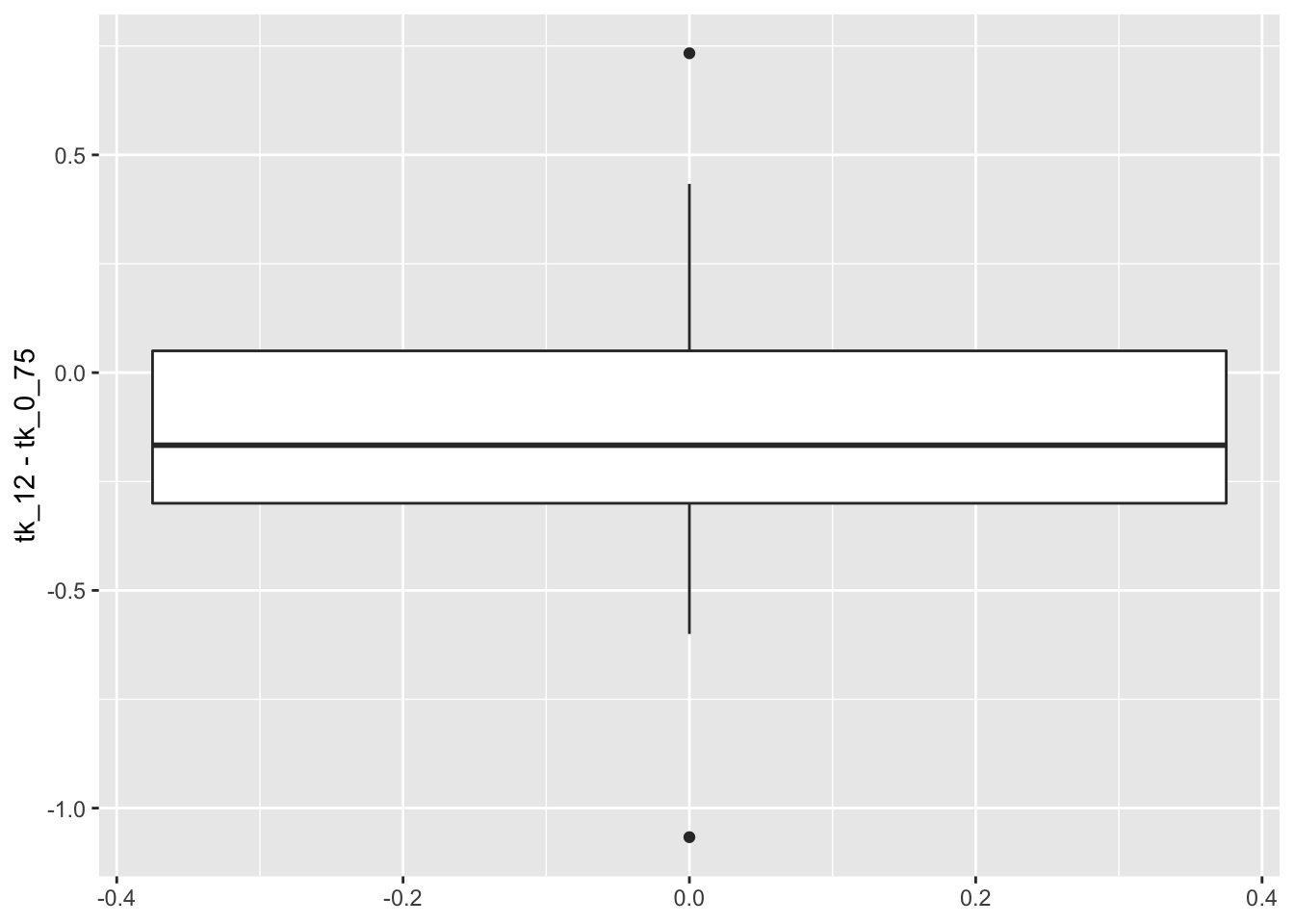
This looks plausibly normal, so let’s do the paired t-test.

t.test(cows_small$tk_12, cows_small$tk_0_75, paired = TRUE)

## 
##  Paired t-test
## 
## data:  cows_small$tk_12 and cows_small$tk_0_75
## t = -1.5118, df = 18, p-value = 0.1479
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -0.31023781  0.05058868
## sample estimates:
## mean of the differences 
##              -0.1298246

We find a 95 percent confidence interval for the difference in the means to be $[-0.31, 0.05]$, and we do not reject $H_0$ at the $\alpha = .05$ level ($p$ = .1479). We cannot conclude that there is a difference in the mean temperature change associated with the two nozzles.

7.7 Type II errors and power

Up to this point, we have been concerned about the probability of rejecting the null hypothesis when the null hypothesis is true. There is another type of error that can occur, however, and that is failing to reject the null hypothesis when the null hypothesis is false. A type I error is rejecting the null when it is true, and a type II error is failing to reject the null when it is false. The power of a test is defined to be one minus the probability of a type II error, which is the probability of correctly rejecting the null hypothesis.

One issue that arises is that the null hypothesis is (usually) a simple hypothesis; that is, it consists of a complete specification of parameters, while the alternative hypothesis is often a composite hypothesis; that is, it consists of parameters in a range of values. Therefore, when we say the null hypothesis is false, we are not completely specifying the distribution of the population. For this reason, the type II error is a function that depends on the value of the parameter(s) in the alternative hypothesis.

Let’s look at the heart rate example using normtemp. Suppose that our null hypothesis is that the mean heart rate of healthy adults is 80 beats per minute. (The American Heart Association says normal is from 60-100.) Our alternative hypothesis is that the mean heart rate of healthy adults is not 80 beats per minute. We take a sample of size 130. What is the probability of a type II error? Well, we can’t do that yet, because we don’t know the standard deviation of the underlying population or the $\alpha$ level of the test. Since the range of values according to AHA is between 60 and 100, which I interpret to mean that about 99% of healthy adults will fall in this range, we will estimate the standard deviation to be (100 - 60)/6 = 6.67. Next, we will fix a value for the alternative hypothesis. Let’s compute the probability of a type II error when the true mean is 70 beats per minute.

It is possible to do this by hand using the non-central parameter ncp argument of pt, but let’s do it using simulation. We start by taking a sample of size 130 from a normal distribution with mean 78 and standard deviation 6.67. We compute the t statistic and determine whether we would reject $H_0$. We assume $\alpha = .01$.

dat <- rnorm(130, 78, 6.67)
t_stat <- (mean(dat) - 80) / (sd(dat) / sqrt(130))
t_stat

## [1] -3.69226

qt(.005, 129) # critical value

## [1] -2.614479

Since t_stat is less than qt(.005, 129) we would (correctly) reject the null hypothesis. Easier would be to use the built in R function t.test to perform the test.

dat <- rnorm(130, 78, 6.67)
t.test(dat, mu = 80)$p.value > .01

## [1] FALSE

Next, we compute the percentage of times that the $p$-value of the test is greater than .01. That is the percentage of times that we have made a type II error, and will be our estimate for the probability of a type II error.

simdata <- replicate(10000, {
  dat <- rnorm(130, 78, 6.67)
  t.test(dat, mu = 80)$p.value > .01
})
mean(simdata)

## [1] 0.2172

We get about a 0.2172 chance for a type II error in this case.

There is a built-in R function which will make this computation for you, called power.t.test. It has the following arguments:

n the number of samples
delta the difference between the null and alternative mean
sd the standard deviation of the population
sig.level the $\alpha$ significance level of the test
power this is one minus the probability of a type II error
type either one.sample, two.sample or paired, default is two
alternative two.sided or one.sided, default is two

The function works by specifying four of the first five parameters, and the function then solves for the unspecified parameter. For example, if we wish to re-do the above simulation using power.t.test, we would use the following.

power.t.test(n = 130, delta = 2, sd = 6.67, sig.level = .01, type = "one")

## 
##      One-sample t test power calculation 
## 
##               n = 130
##           delta = 2
##              sd = 6.67
##       sig.level = 0.01
##           power = 0.7878322
##     alternative = two.sided

We get power is .7878322, so the probability of a type II error is one minus that, or

1 - .7878322

## [1] 0.2121678

which is close to what we computed in the simulation.

A traditional approach in designing experiments is to specify the significance level and power, and use a simulation or power.t.test to determine what sample size is necessary to achieve that power. In order to do so, we must estimate the standard deviation of the underlying population and we must specify the effect size that we are interested in. Sometimes there is an effect size in the literature that can be used. Other times, we can pick a size that would be clinically significant (as opposed to statistically significant). Think about it like this: if the true mean body temperature of healthy adults is 98.59, would that make a difference in treatment or diagnosis? No. What about if it were 100? Then yes, that would make a significant difference in diagnoses! It is subjective and can be challenging to specify what delta to provide, but we should provide one that would make a significant difference in some context.

Let’s look at the body temperature study. We have as our null hypothesis that the mean temperature of healthy adults is 98.6 degrees. We estimate the standard deviation of the underlying population to be 0.3 degrees. After consulting with our subject area expert, we decide that a clinically significant difference from 98.6 degrees would be 0.2 degrees. That is, if the true mean is 98.4 or 98.8 then we want to detect it with power 0.8. The sample size needed is

power.t.test(delta = 0.2, sd = .3, sig.level = .01, power = 0.8, type = "one")

## 
##      One-sample t test power calculation 
## 
##               n = 29.64538
##           delta = 0.2
##              sd = 0.3
##       sig.level = 0.01
##           power = 0.8
##     alternative = two.sided

We would need to collect 30 samples in order to have an appropriately powered test.

7.7.1 Effect size

We used the word “effect size” above, without really saying what we mean. A common measure of the effect size is given by \[ d = \frac{\overline{x} - \mu_0}{S}, \] the difference between the sample mean and the mean from the null hypothesis, divided by the sample standard deviation. The parametrization of power.t.test is redundant in the sense that the power of a test only relies delta and sd through the effect size $d$. As an example, we note that when delta = .1 and sd = .5 the effect size is 0.2, as it also is when delta = .3 and sd = 1.5. Both of these give the same power:

power.t.test(n = 30, delta = .3, sd = 1.5, sig.level = .05, type = "one")

## 
##      One-sample t test power calculation 
## 
##               n = 30
##           delta = 0.3
##              sd = 1.5
##       sig.level = 0.05
##           power = 0.1839206
##     alternative = two.sided

power.t.test(n = 30, delta = .1, sd = .5, sig.level = .05, type = "one")

## 
##      One-sample t test power calculation 
## 
##               n = 30
##           delta = 0.1
##              sd = 0.5
##       sig.level = 0.05
##           power = 0.1839206
##     alternative = two.sided

It is common to report the effect size, especially when there is statistical significance. The following chart gives easily interpretable values for $d$. The adjectives associated with effect size should be taken with a grain of salt, though, and they do not replace having a domain area understanding of effect.

Table 7.1: Descriptors of Effect Sizes
Effect Size	d
Very Small	0.01
Small	0.20
Medium	0.50
Large	0.80
Very Large	1.20

If you are designing an experiment and you aren’t sure what effect size to choose for power computation, you can use the descriptors to give yourself an idea of what size you want to detect, with the understanding that this varies widely between disciplines.

You do not want your test to be underpowered for two reasons. First, you likely will not reject the null hypothesis in instances where you would like to be able to do so. Second, when effect sizes are estimated using underpowered tests, they tend to be overestimated. This leads to a reproducibility problem, because when people design further studies to corroborate your study, they are using an effect size that is too high. Let’s run some simulations to verify. We assume that we have an experiment with power 0.2.

power.t.test(delta = 0.2, sd = 1, sig.level = .05, power = 0.25, type = "one")

## 
##      One-sample t test power calculation 
## 
##               n = 43.24862
##           delta = 0.2
##              sd = 1
##       sig.level = 0.05
##           power = 0.25
##     alternative = two.sided

This says when $d = 0.2$, we need 43 samples for the power to be 0.25. Remember, this is not recommended! We use simulation to estimate the percentage of times that the null hypothesis is rejected. We assume we are testing $H_0: \mu = 0$ versus $H_a: \mu \not=0$.

simdata <- replicate(10000, {
  dat <- rnorm(43, 0.2, 1)
  t.test(dat, mu = 0)$p.value
})
mean(simdata < .05)

## [1] 0.2494

And we see that indeed, we get about 25%, which is what power.t.test predicted. Note that the true effect size is 0.2. The estimated effect size from tests which are significant is given by:

simdata <- replicate(10000, {
  dat <- rnorm(43, 0.2, 1)
  ifelse(t.test(dat, mu = 0)$p.value < .05,
    abs(mean(dat)) / sd(dat),
    NA
  )
})
mean(simdata, na.rm = TRUE)

## [1] 0.4068898

We see that the mean estimated effect size is double the actual effect size, so we have a biased estimate for effect size. If we have an appropriately powered test, then this bias is much less.

power.t.test(delta = 0.2, sd = 1, sig.level = .05, power = 0.8, type = "one")

## 
##      One-sample t test power calculation 
## 
##               n = 198.1513
##           delta = 0.2
##              sd = 1
##       sig.level = 0.05
##           power = 0.8
##     alternative = two.sided

simdata <- replicate(10000, {
  dat <- rnorm(199, 0.2, 1)
  ifelse(t.test(dat, mu = 0)$p.value < .05,
    abs(mean(dat)) / sd(dat),
    NA
  )
})
mean(simdata, na.rm = TRUE)

## [1] 0.2252274

Vignette: A Permutation Test

What do you do when you aren’t sure whether your data comes from a population that satisfies the assumptions of a $t$-test? One popular alternative is the permutation test . If we imagine that there was no difference between the two populations, then the assignments of the grouping variables can be considered random. A permutation test takes random permutations of the grouping variables, and re-computes the test statistic. Under $H_0$: the response is independent of the grouping, we should often get values as extreme as the value obtained in the sample. We reject $H_0$ if the proportion of times we get something as unusual as in the sample is less than $\alpha$/

Let’s consider the brake data that we studied in this chapter, except this time we consider latency_p1, the time for the subject to hit the brake after seeing a red light. We load the data via

brake <- fosdata::brake

We compute the mean latency for releasing the brake of the older group minus the mean of the younger group.

mean_brake <- mean(brake$latency_p1[brake$age_group == "Old"]) - mean(brake$latency_p1[brake$age_group == "Young"])
mean_brake

## [1] -10.94183

We get that the older group was on average a bit faster than the younger group. Let’s also look at a boxplot.

ggplot(brake, aes(x = age_group, y = latency_p1)) + 
  geom_boxplot(outlier.size = -1) +
  geom_jitter(height = 0, width = 0.2)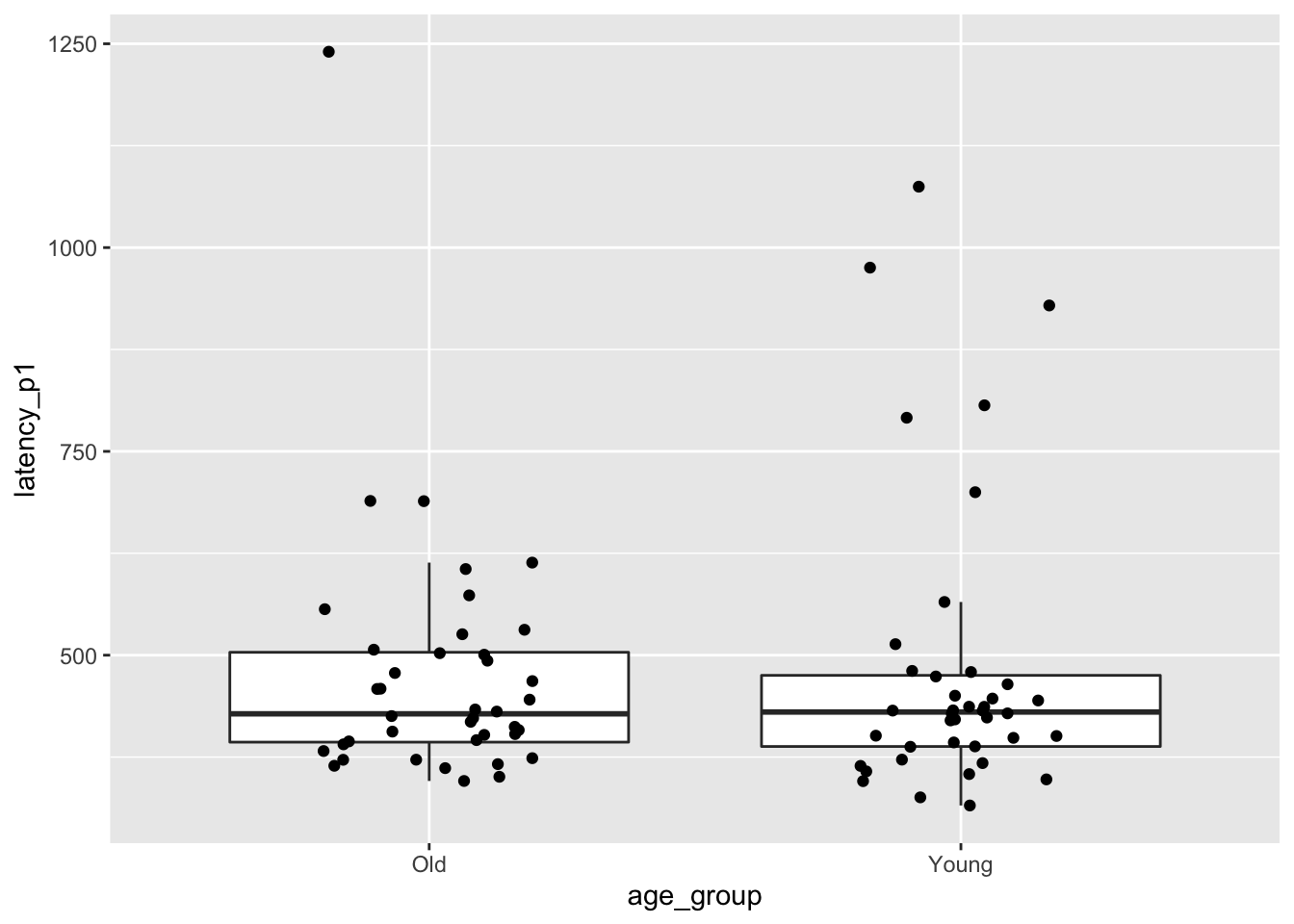

We again see that the data is skew, so there should be at least some hesitation to use a $t$-test.

Instead, we permute the age groups many times and recompute the test statistic.

perm_test <- replicate(10000, {
  brake$age_group <- sample(brake$age_group) #this randomly permutes the age groups
  mean(brake$latency_p2[brake$age_group == "Old"]) - mean(brake$latency_p2[brake$age_group == "Young"])
})
hist(perm_test)
abline(v = mean_brake, lty = 2)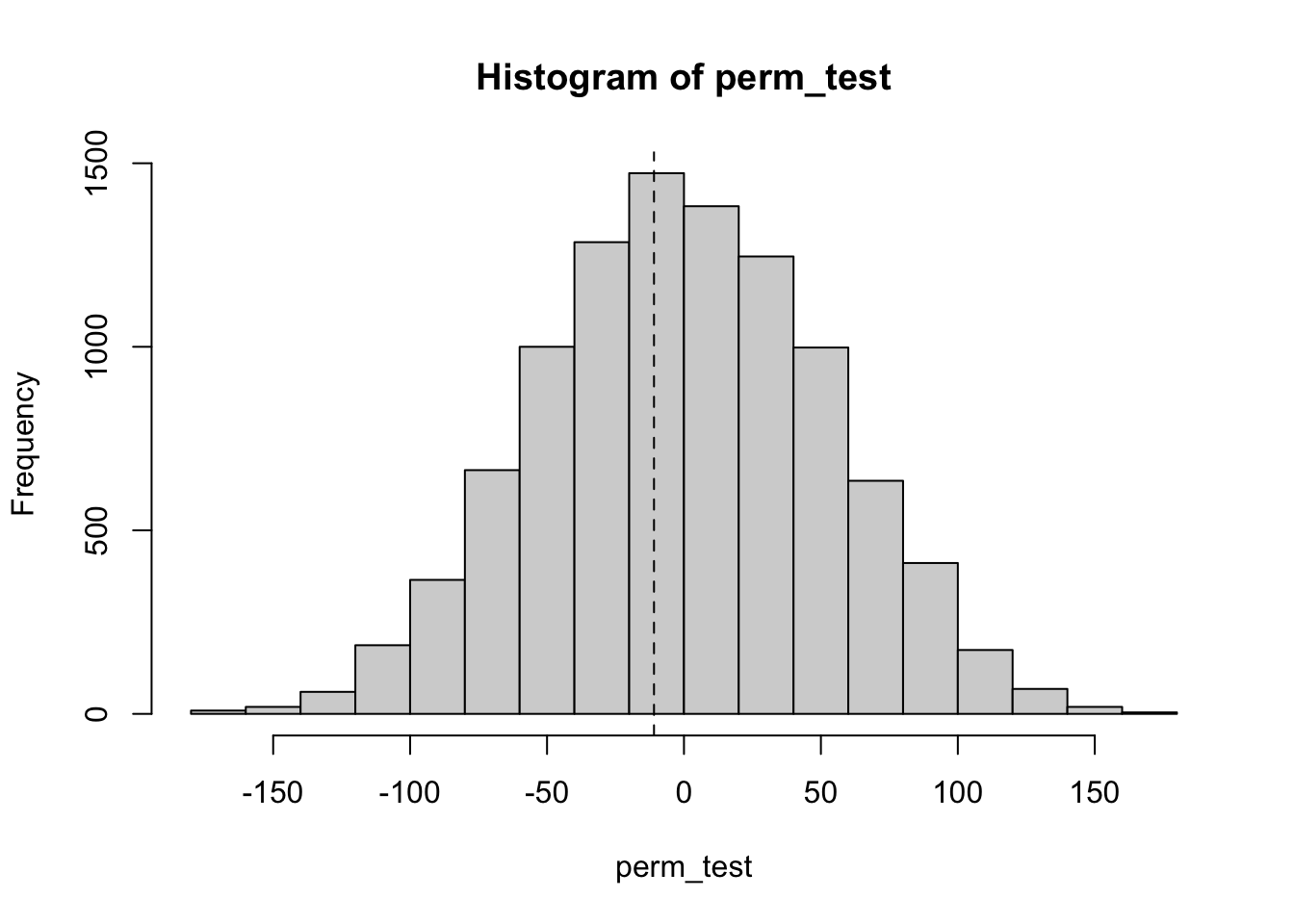

We see from the histogram that it is not at all unusual to get a value of $-11$. To get a $p$-value, we compute

2 * mean(perm_test < mean_brake) #since mean_brake < 0, Otherwise, we would do perm_test > mean_brake

## [1] 0.8462

We have a $p$-value of .8456, and we would not reject the null hypothesis.

Exercises

Use the built in R dataset precip to compute a 99% confidence interval for the mean rainfall in US cities.
Consider the brake dataset discussed in the chapter. Recall that latency_p2 is the time it takes subjects to release the pedal once they have pressed it and the car has started to accelerate rather than decelerate. Find a 95 percent confidence interval for the P2 latency for young drivers based on the data.
Michelson’s measurements of the speed of light. Get the file data/michelson_light_speed.csv. This file contains two series of measurements of the speed of light made by Albert Michelson in 1879 and 1882. The measurements are given in amounts over 299000 km/s.
1. Find a 95% confidence interval for the speed of light using the 1879 data.
2. Find a 95% confidence interval for the speed of light using the 1882 data.
3. Which set of data has a higher SD? Which set has a larger sample size? Which confidence interval is wider? Explain how these three questions are related.
4. The modern accepted value for the speed of light is 299792.5km/s. Do the 95% confidence intervals from parts a. and b. contain the true value?
5. Speculate as to why the 1879 data might give a confidence interval that does not contain the true value of the speed of light.
1. Choose 10 random values of $X$ having the Normal(4, 1) distribution. Use t.test to compute the 95% confidence interval for the mean. Is 4 in your confidence interval?
2. Replicate the experiment in part a 10,000 times and compute the percentage of times the population mean 4 was included in the confidence interval.
3. Repeat part b, except sample your 10 values when $X$ has the Exponential(1/4) distribution. What is the mean of $X$? What percentage of times did the confidence interval contain the population mean? It’s not 95%. Why?
4. Now repeat b. and c. using 100 values of $X$ to make each confidence interval. What percentage of times did the confidence interval contain the population mean? Compare to part c.
Compute $P(z > 2)$, where z is the standard normal variable. Compute $P(t > 2)$ for $t$ having Student’s $t$ distribution with each of 40, 20, 10, and 5 degrees of freedom. How does the DF affect the area in the tail of the $t$ distribution?
Consider the react data set from ISwR. Find a 98% confidence interval for the mean difference in measurements of the tuberculin reaction. Does the mean differ significantly from zero according to a t-test? Interpret.
Each of these studies has won the prestigious Ig Nobel prize. For each, state the null hypothesis.
1. Marina de Tommaso, Michele Sardaro, and Paolo Livrea, for measuring the relative pain people suffer while looking at an ugly painting, rather than a pretty painting, while being shot (in the hand) by a powerful laser beam.
2. Atsuki Higashiyama and Kohei Adachi, for investigating whether things look different when you bend over and view them between your legs.
3. Patricia Yang, David Hu, Jonathan Pham, and Jerome Choo, for testing the biological principle that nearly all mammals empty their bladders in about 21 seconds.
Mammograms are usually read by two different clinicians, but it would be more efficient to use one clinician plus computer aided detection. A study in NEJM reported: The proportion of cancers detected was 199 of 227 (87.7%) for double reading and 198 of 227 (87.2%) for single reading with computer-aided detection (P=0.89). The overall recall rates were 3.4% for double reading and 3.9% for single reading with computer-aided detection; the difference between the recall rates was small but significant.
1. Is there a significant difference between the detection rates?
2. When the clinicians see something on the mammogram, they recall patients for a follow-up. What was the difference between the recall rates?
3. How could such a small difference be significant?
Consider the bp.obese data set from ISwR. It contains data from a random sample of Mexican-American adults in a small California town. Consider only the blood pressure data for this problem. Normal diastolic blood pressure is 120. Is there evidence to suggest that the mean blood pressure of the population differs from 120? What is the population in this example?
Again for the bp.obese data set; consider now the obese variable. What is the natural null hypothesis? Is there evidence to suggest that the obesity level of the population differs from the null hypothesis?
For the bp.obese data set, is there evidence to suggest that the mean blood pressure of Mexican-American men is different from that of Mexican-American women in this small California town? Would it be appropriate to generalize your answer to the mean blood pressure of men and women in the USA?
Add a problem about MASS::anorexia that used to be in the text.
Consider the ex0112 data in the Sleuth3 package. The researchers randomly assigned 7 people to receive fish oil and 7 people to receive regular oil, and measured the decrease in their diastolic blood pressure. Is there sufficient evidence to conclude that the mean decrease in blood pressure of patients taking fish oil is different from the mean decrease in blood pressure of those taking regular oil?¹⁹
Consider the ex0333 data in the Sleuth3 package This is an observational study of brain size and litter size in mammals. Create a boxplot of the brain size for large litter and small litter mammals. Does the data look normal? Create a histogram (or a qqplot if you know how to do it). Repeat after taking the logs of the brain sizes. Is there evidence to suggest that there is a difference in mean brain sizes of large litter animals and small litter animals?
Consider the case0202 data in the Sleuth3 package This data is from a study of twins, where one twin was schizophrenic and the other was not. The researchers used magnetic resonance imaging to measure the volumes (in $\text{cm}^3$) of several regions and subregions of the twins’ brains. State and carry out a hypothesis test that there is a difference in the volume of these brain regions between the Affected and the Unaffected twins.
Consider the cows_small data set in the fosdata package that was discussed in this chapter. Is there sufficient evidence to conclude that the mean temperature change associated with the TK-0.75 nozzle is less than the mean temperature change associated with not spraying the cows at all; that is, with the control?
The authors in the wrist data paper ²⁰ did a power analysis in order to determine sample size. They wanted a power of 80 percent at the $\alpha = .05$ level, and they assumed that 30 percent of their patients would drop out. Previous studies had shown that the standard deviation of the prwe12m variable would be about 14. They concluded that they needed 40 participants in each group. What difference in means did they use in their power computation? (You can check your answer by looking up their paper.)
The authors in the wrist data paper ²¹ used the fosdata::wrist data set to find a confidence 95 percent confidence interval for the difference in the mean of prwe12m between the functional cast position and the volar-flexion and ulnar deviation cast position. They assumed equal variances in the two populations to find the 95 percent confidence interval.
1. Find the 95 percent confidence interval of the mean difference assuming equal variances, and compare it to the value that the authors found in the paper.
2. Was assuming equal variance justified?
This exercise explores how the t-test changes when data values are transformed. (See also Exercise 8.3)
1. Suppose you wish to test $H_0: \mu = 0$ versus $H_a: \mu \not = 0$ using a t-test You collect data $x_1 = -1,x_2 = 2,x_3 = -3,x_4 = -4$ and $x_5 = 5$. What is the $p$-value?
2. Now, suppose you multiply everything by 2: $H_0: \mu = 0$ versus $H_a: \mu\not = 0$ and your data is $x_1 = -2,x_2 = 4,x_3 = -6,x_4 = -8$ and $x_5 = 10$. What happens to the $p$-value? (Try to answer this without using R. Check your answer using R, if you must.)
3. Now, suppose you square the magnitudes of everything. $H_0: \mu = 0$ versus $H_a: \mu \not= 0$, and your data is $x_1 = -1,x_2 = 4,x_3 = -9,x_4 = -16$ and $x_5 = 25$. What happens to the $p$-value?
A Nature article investigated the protein caloric content in the edible skeletal muscle mass in a typical adult male human based on an analysis of 4 human males to be 19551, see table S5 here for details.

A previous article had estimated the protein caloric content in the edible skeletal muscle mass in a typical adult human male to be 18,000 calories. If you wished to test whether the true mean protein caloric content in the edible skeletal muscle mass in a typical adult human male is 18,000 calories, what sample size would you choose in order to have a power of 80% when $\alpha = .01$ at an effect size indicated by the Nature study?
The purpose of this exercise is to examine the effect of sample size, effect size, and significance level on the power of a test when the starting point is at about a power of .5.
1. Fix an effect size of $d = .2$ and a significance level of $\alpha = .05$, and compute the power of a two-sided one-sample t-test for $n = 200$ and $n = 400$. What happens to the power?
2. Fix a significance level of $\alpha - .05$ and $n = 200$, and compute the power of a two-sided one-sample t-test for $d = .2$ and $d = .4$. What happens to the power?
3. Fix $n = 200$ and an effect size of $d = .2$, and compute the power of a two-sided one-sample t-test for $\alpha = .05$ and $\alpha = .1$. What happens to the power?
$\star$ This problem explores how the $t$ test behaves in the presence of an outlier.

Create a data set of 20 random values $x_1,\ldots,x_{20}$ with the standard normal distribution. Replace $x_{20}$ with the number 1000. Perform a $t$ test with $H_0 : \mu = 5$, and observe the $t$ value. It should be quite close to 1. Is the $t$-test able to find a significant difference between the mean of this data and 5?

The next parts of this problem ask you to prove that $t$ is always close to 1 in the presence of a large outlier.
Assume that $x_1,\ldots,x_{n-1}$ are not changing, but $x_n$ varies. Let $\overline{X} = \frac 1n \sum_{i=1}^n x_i$ as usual. Show that \[ \lim_{x_n\to\infty} \frac{\overline{X}}{x_n} = \frac{1}{n}. \]
Let the sample variance be $S^2 = \frac 1{n-1}\sum_{i=1}^n (x_i - \overline{X})^2$ as usual. Show that \[ \lim_{x_n\to\infty} \frac{S^2}{x_n^2} = \frac{1}{n}. \]
Finally show that \[ \lim_{x_n\to\infty} \frac{\overline{X} - \mu_0}{S/\sqrt{n}} = 1, \] where $\mu_0$ is any real number. (Hint: divide top and bottom by $x_n$, then use parts b and c).
What does this say about the ability of a $t$ test to reject $H_0: \mu = \mu_0$ at the $\alpha = .05$ level as $x_n\to \infty$?

Re-do the analysis of latency_p2 in the brake data set with the largest older outlier removed. Does removing the largest older outlier change the conclusion of your test at the $\alpha = .05$ level?

These data are derived from a dataset presented in Mackowiak, P. A., Wasserman, S. S., and Levine, M. M. (1992), “A Critical Appraisal of 98.6 Degrees F, the Upper Limit of the Normal Body Temperature, and Other Legacies of Carl Reinhold August Wunderlich,” Journal of the American Medical Association, 268, 1578-1580. Data were constructed to match as closely as possible the histograms and summary statistics presented in that article. Additional information about these data can be found in the “Datasets and Stories” article “What’s Normal? – Temperature, Gender, and Heart Rate” in the Journal of Statistics Education (Shoemaker 1996).
↩︎
The answers to problems from the Sleuth3 package are readily available on-line. We strongly suggest that you first do your absolute best to answer the problem on your own before you search for answers!↩︎
Raittio L, Launonen AP, Hevonkorpi T, Luokkala T, Kukkonen J, Reito A, et al. (2020) Two casting methods compared in patients with Colles’ fracture: A pragmatic, randomized controlled trial. PLoS ONE 15(5): e0232153.↩︎
Raittio L, Launonen AP, Hevonkorpi T, Luokkala T, Kukkonen J, Reito A, et al. (2020) Two casting methods compared in patients with Colles’ fracture: A pragmatic, randomized controlled trial. PLoS ONE 15(5): e0232153.↩︎

Foundations of Statistics with R