Chapter 8 Rank Based Tests

In Chapter 7 we saw how to create confidence intervals and perform hypothesis testing on population means. One of our takeaways, though, was that our techniques were inappropriate to use on populations with big outliers. In this section, we discuss rank based tests that can be used, and are still effective, when the population has these outliers. When the underlying population is normal, then the rank based tests will have slightly lower power than their t.test counterpart, but in many cases they are more powerful.

The tests discussed in the chapter can also be used when the measured quantity is ordinal rather than numeric.

8.1 One sample Wilcoxon Signed Rank Test

In this test, we will be testing \(H_0: m = m_0\) versus \(H_a: m\not= m_0\), where \(m\) is the median of the underlying population. We will assume that the data is centered symmetrically around the median (so that the median is also the mean). There can be outliers, bimodality or any kind of tails.

Let’s look at how the test works by hand by examining a simple, made up data set. Suppose you wish to test

\[ H_0: m = 6 \qquad {\rm vs} \qquad H_a: m\not=6 \] You collect the data \(x_1 = 15, x_2 = 7, x_3 = 3, x_4 = 10\) and \(x_5 = 13\). The test works as follows:

  1. Compute \(y_i = x_i - m_0\) for each \(i\). We get \(y_1 = 9, y_2 = 1, y_3 = -3, y_4 = 4\) and \(y_5 = 7\).
  2. Let \(R_i\) be the rank of the absolute value of \(y_i\). That is, \(R_1 = 5, R_2 = 1, R_3 = 2, R_4 = 3, R_5 = 4\) since \(R_1\) is largest, \(R_2\) is smallest, etc.
  3. Let \(r_i\) be the signed rank of \(R_i\); i.e. \(r_i = R_i \times {\rm sign} (y_i)\). namely \(r_1 = 5, r_2 = 1, r_3 = -2, r_4 = 3, r_5 = 4\)
  4. Add all of the positive ranks. We get \(r_1 + r_2 + r_4 + r_5 = 13\). That is the test statistic for this test, and it is traditionally called \(V\).
  5. Compute the P-value for the test, which is the probability that we get a test statistic \(V\) which is this, or more, unlikely under the assumption of \(H_0\).

In order to perform the last step, we need to understand the sampling distribution of \(V\), under the assumption of the null hypothesis, \(H_0\). The ranks of our five data points will always be the numbers 1,2,3,4, and 5. When \(H_0\) is true, each data point is equally likely to be positive or negative, and so will be included in the rank-sum half of the time. So, the expected value \[ E(V) = \frac{1}{2}\cdot 1 + \frac{1}{2}\cdot 2 + \frac{1}{2}\cdot 3 + \frac{1}{2}\cdot 4 + \frac{1}{2}\cdot5 = \frac{15}{2} = 7.5 \] In our example, \(V = 13\), which is 5.5 away from the expected value of 7.5.

For the probability distribution of \(V\), we list all \(2^5 = 32\) possibilities of how the ranks could be signed. Since we have assumed that the distribution is centered about its mean, each of the possibilities are equally likely. Therefore, we can compute the proportion that lead to a test statistic at least 5.5 away from the expected value of 7.5.

Table 8.1: All possible sums of positive signed ranks
r1 r2 r3 r4 r5 Sum of positive ranks Far from 7.5?
-1 -2 -3 -4 -5 0 TRUE
-1 -2 -3 -4 5 5 FALSE
-1 -2 -3 4 -5 4 FALSE
-1 -2 -3 4 5 9 FALSE
-1 -2 3 -4 -5 3 FALSE
-1 -2 3 -4 5 8 FALSE
-1 -2 3 4 -5 7 FALSE
-1 -2 3 4 5 12 FALSE
-1 2 -3 -4 -5 2 TRUE
-1 2 -3 -4 5 7 FALSE
-1 2 -3 4 -5 6 FALSE
-1 2 -3 4 5 11 FALSE
-1 2 3 -4 -5 5 FALSE
-1 2 3 -4 5 10 FALSE
-1 2 3 4 -5 9 FALSE
-1 2 3 4 5 14 TRUE
1 -2 -3 -4 -5 1 TRUE
1 -2 -3 -4 5 6 FALSE
1 -2 -3 4 -5 5 FALSE
1 -2 -3 4 5 10 FALSE
1 -2 3 -4 -5 4 FALSE
1 -2 3 -4 5 9 FALSE
1 -2 3 4 -5 8 FALSE
1 -2 3 4 5 13 TRUE
1 2 -3 -4 -5 3 FALSE
1 2 -3 -4 5 8 FALSE
1 2 -3 4 -5 7 FALSE
1 2 -3 4 5 12 FALSE
1 2 3 -4 -5 6 FALSE
1 2 3 -4 5 11 FALSE
1 2 3 4 -5 10 FALSE
1 2 3 4 5 15 TRUE

The last column in Table 8.1 is TRUE if the sum of positive ranks is greater than or equal to 13 or less than or equal to 2. As you can see, we have 6 of the 32 possibilities are at least as far away from the test stat as our data, so the \(p\)-value would be \(\frac{6}{32} = .1875\).

Let’s check it with the built in R command.

wilcox.test(c(15,7,3,10,13), mu = 6)
## 
##  Wilcoxon signed rank exact test
## 
## data:  c(15, 7, 3, 10, 13)
## V = 13, p-value = 0.1875
## alternative hypothesis: true location is not equal to 6

We see that our test statistic \(V = 13\) and the \(p\)-value is 0.1875, just as we calculated.

In general, if you have \(n\) data points, the expected value of \(V\) is \(E(V) = \frac{n(n+1)}{4}\) (Exercise 1) To deal with ties, give each data point the average rank of the tied values.

The sampling distribution of the test statistic \(V\) under the null hypothesis is a built-in R distribution with root signrank. As usual, this function has prefixes d p q and r, which correspond to the pmf, cdf, quantile function and random generator, respectively. So, in the above example, we also could have computed the \(p\)-value as the probability that \(V\) is in \(\{0, 1, 2, 13, 14, 15\}\) as

sum(dsignrank(c(0:2, 13:15), 4))
## [1] 0.1875

Let’s examine the pmf of the test statistic when we have sample sizes of 10 and 30, in which case the expected values of the test statistic will be 27.5 and 232.5.

n <- 10
x_vals <- 0:55
for_plot <- data.frame(x = x_vals,
                       probs = dsignrank(x_vals, n))
ggplot(for_plot, aes(x = x, y = probs)) +
  geom_bar(stat = "identity") +
  ggtitle(label = "pmf of V when n = 10")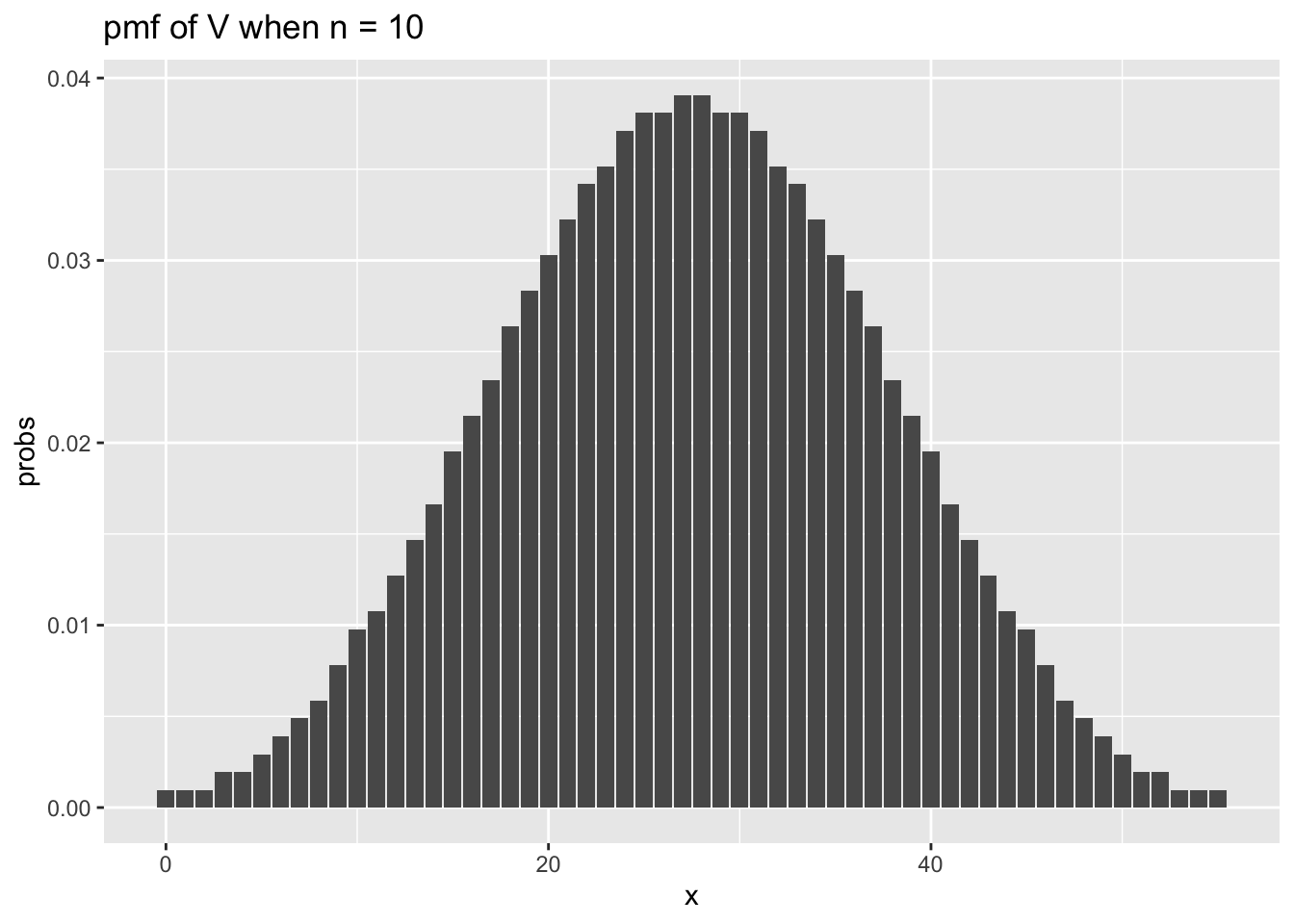 

n <- 30
x_vals <- 83:381
for_plot <- data.frame(x = x_vals,
                       probs = dsignrank(x_vals, n))
ggplot(for_plot, aes(x = x, y = probs)) +
  geom_bar(stat = "identity") +
  ggtitle(label = "pmf of V when n = 30")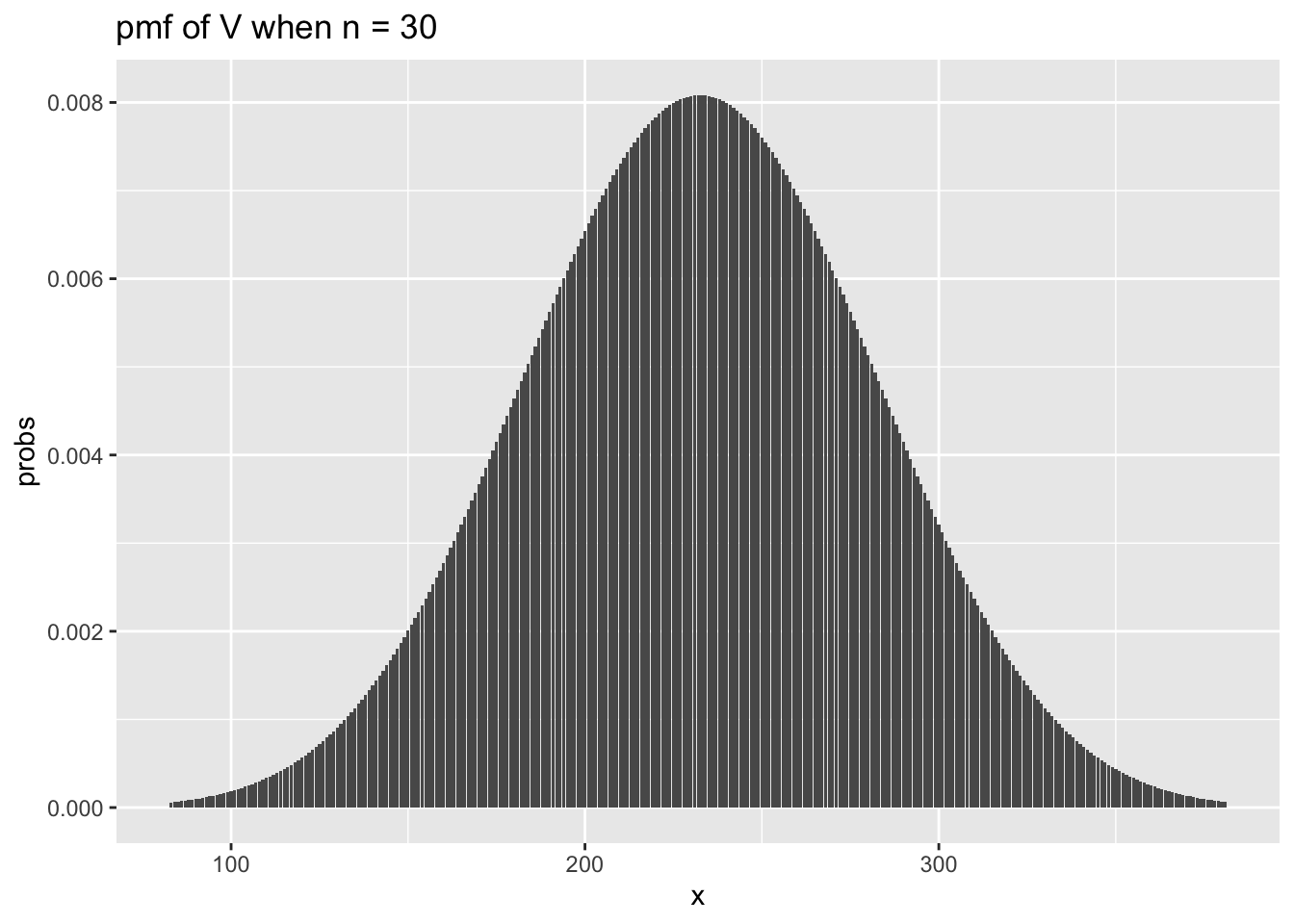

We see that the curves look very similar to a normal curve. In fact, it can be shown that when \(n\) is large, the sampling distribution of \(V\) is approximately normal with mean \(\frac{n (n + 1)}{4}\) and variance \(\frac{n(n+1)(2n+1)}{24}\). To check this, let’s super-impose the plot of a normal with that mean and variance on the plot of psignrank.

mu <- 31 * 30/4
sigma <- sqrt(30 * 31 * 61/24)
ggplot(for_plot, aes(x = x, y = probs)) +
  geom_bar(stat = "identity") +
  ggtitle(label = "pmf of V when n = 30", subtitle = "With a super-imposed normal curve") +
  stat_function(fun = ~ dnorm(.x, mu, sigma), color = "red")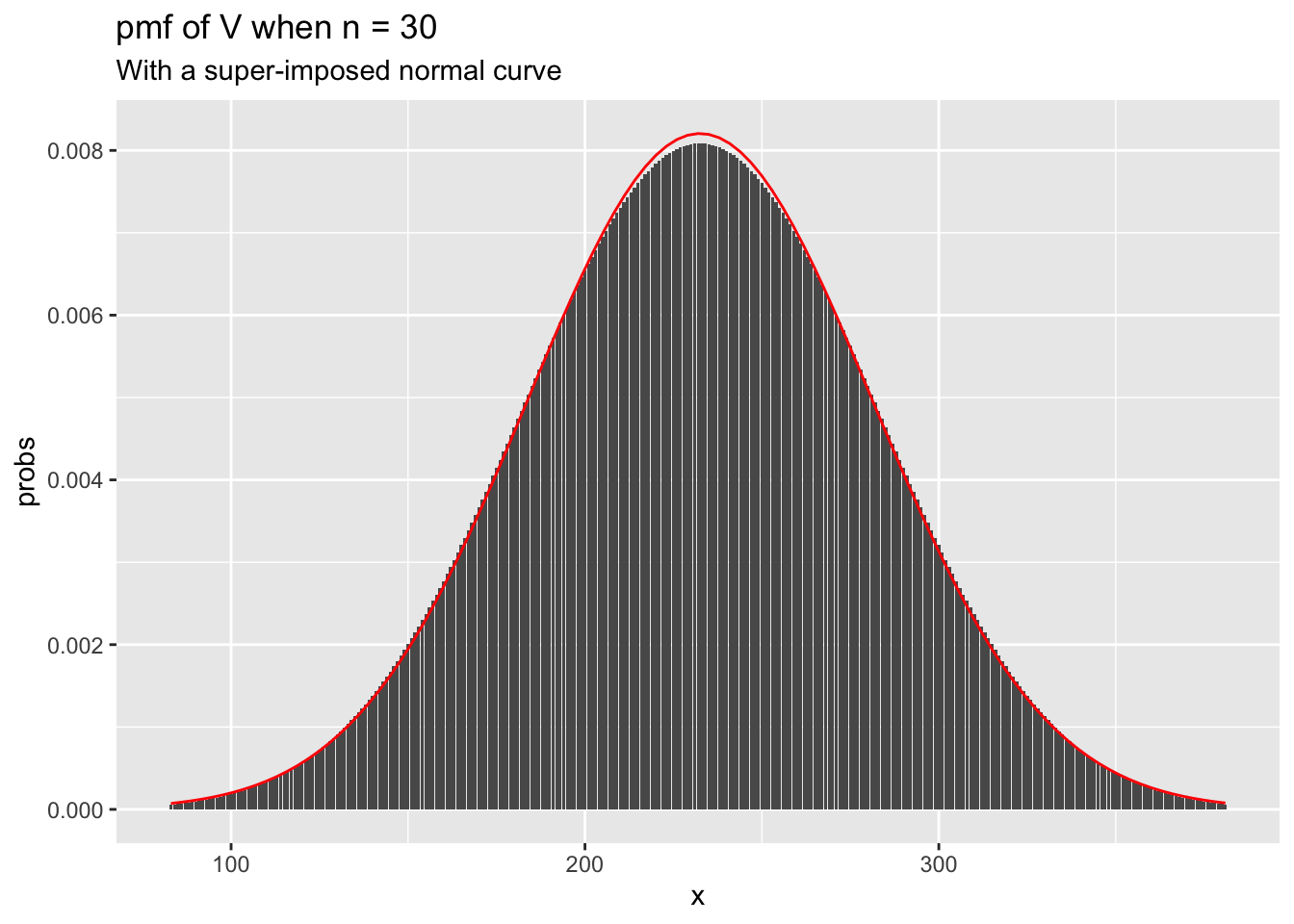

When \(n = 30\), we already have a very close approximation by a normal curve.

Let’s look at some examples. Consider the normtemp data set in the fosdata package. Recall that this data is the gender, body temperature and heart rate of 130 patients. We are interested in whether the mean or median body temperature is 98.6. A t test looks like this:

normtemp <- fosdata::normtemp
t.test(normtemp$temp, mu = 98.6)
## 
##  One Sample t-test
## 
## data:  normtemp$temp
## t = -5.4548, df = 129, p-value = 2.411e-07
## alternative hypothesis: true mean is not equal to 98.6
## 95 percent confidence interval:
##  98.12200 98.37646
## sample estimates:
## mean of x 
##  98.24923

and we got a p-value of \(2 \times 10^{-7}\). If we instead were to do a Wilcoxon test, we get

wilcox.test(normtemp$temp, mu = 98.6)
## 
##  Wilcoxon signed rank test with continuity correction
## 
## data:  normtemp$temp
## V = 1774.5, p-value = 1.174e-06
## alternative hypothesis: true location is not equal to 98.6

The p-value still leads to the same conclusion at most reasonable \(\alpha\) levels, but it is about 5 times as large as the \(t\)-test. Each test is estimating the probability that we will obtain data this unlikely or more unlikely, given that the null hypothesis is true. But they are summarizing what it means to be “this unlikely” in different ways. If the underlying population really is normal, then the \(t\)-test will be more likely to correctly determine that we can reject \(H_0\) when we need to.

(p <- sum(replicate(10000,t.test(rnorm(50),mu=.5)$p.value)< .05))
## [1] 9338

Here, we see that t.test correctly rejects \(H_0\) 93.38% of the time. Doing the same thing for Wilcoxon:

(p <- sum(replicate(10000,wilcox.test(rnorm(50),mu=.5)$p.value)< .05))
## [1] 9158

We see that Wilcoxon correctly rejects \(H_0\) 91.58% of the time. So, if you have reason to think that your data is normal or symmetric with not too heavy tails, then you will get slightly better results using t.test. If it is symmetric but with heavy tails or especially with outliers, then Wilcoxon will perform better. See Section 8.3 for more simulations and discussion.

8.2 Two Sample Wilcoxon Rank Sum test

Next, we will be considering wilcox.test when we wish to compare the samples from two distributions, referred to as the Wilcoxon rank sum test. We no longer need to assume that the populations are symmetric, but we assume that all of the observations are independent. (Later, we will see how we can handle paired data.)

The null hypothesis and alternative hypotheses can be stated as follows.

\(H_0\): the distribution of population 1 is the same as the distribution of population 2.

\(H_a\): the distribution of population 1 is different than the distribution of population 2.

The test statistic that we construct is the following: for each data point \(x\) in Sample 1, we count the number of data points in Sample 2 that are less than \(x\). The total number of “wins” for sample 1 is the test statistic. (Count ties as 0.5.) Under the null hypothesis, the expected value of the test statistic is \[ N_1 N_2 /2. \] Let’s look at a simple example for concreteness.

Suppose that we obtain the following data, which has two observations in group 1 and three observations in group 2.

group value
1 5
1 11
2 0
2 3
2 10

The value \(x = 1\) is bigger than two observations in group 2, while the value \(x = 11\) is larger than three observations in group 2. So, the value of the test statistic is \(W = 2 + 3 = 5\). The expected value of the test statistic is \(2 \times 3 /2 = 3\), so the \(p\)-value of the test is the probability (under the null) of obtaining a test statistic either 5 or larger, or obtaining one that is 1 or smaller, i.e. \(P(|W - 3| \ge 2)\). To compute this probability, we imagine that we have sorted the 5 values from smallest to largest. Under the null hypothesis, each possible arrangement of group 1 and group 2 within the sorted values would be equally likely. There are choose(5,3) = 10 possible permutations of the values, which we list here:

Table 8.2: Possible Permutations of Three 2’s and Two 1’s, with associated test statistic
V1 V2 V3 V4 V5 W
2 2 2 1 1 6
2 2 1 2 1 5
2 1 2 2 1 4
1 2 2 2 1 3
2 2 1 1 2 4
2 1 2 1 2 3
1 2 2 1 2 2
2 1 1 2 2 2
1 2 1 2 2 1
1 1 2 2 2 0

Under the assumption that the distribution of population 1 is the same as the distribution of population 2, each outcome is equally likely. It follows that \(P(|W - 3| \ge 2) = 4/10\).

As with the one-sample test, there are helper functions in R that make computations easier. The sampling distribution of the test statistic \(W\) is in the base R distribution *wilcox, where as always, the prefixes are dpqr for pmf, cdf, quantiles or random sample. For example, if we wish to compute \(P(|W - 3| \ge 2)\) when the two sample sizes are 2 and 3, as above, we could do the following.

sum(dwilcox(c(0, 1, 5, 6), m = 2, n = 3))
## [1] 0.4

Now we examine the distribution of the test statistic when \(m = 5, n = 10\) and when \(m = n = 20\).

m <- 5
n <- 10
x_vals <- 0:52
for_plot <- data.frame(x = x_vals,
                       probs = dwilcox(x_vals,m, n))
ggplot(for_plot, aes(x = x, y = probs)) +
  geom_bar(stat = "identity") +
  ggtitle(label = "pmf of W when m = 5, n = 10")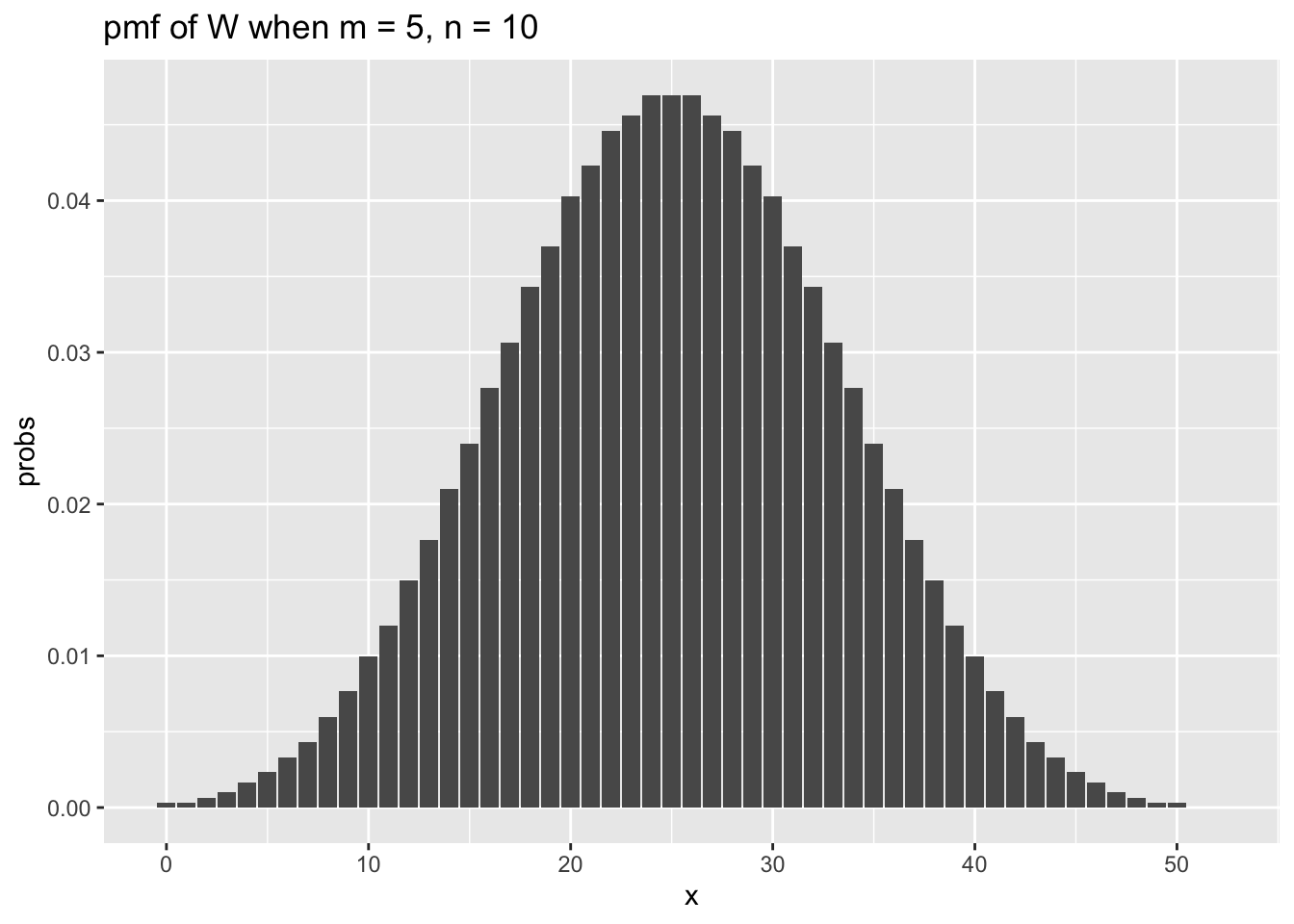 

m <- 20
n <- 20
x_vals <- 50:350
for_plot <- data.frame(x = x_vals,
                       probs = dwilcox(x_vals,m, n))
ggplot(for_plot, aes(x = x, y = probs)) +
  geom_bar(stat = "identity") +
  ggtitle(label = "pmf of W when m = 20, n = 20")

As in the one-sample case, we see that the sampling distribution of the test statistic looks approximately normal when \(n\) and \(m\) are even modestly large. The variance of the test statistic \(W\) is given by \(\frac {mn(m + n + 1)}{12}\), which we use to super-impose a normal pdf on the above plot.

ggplot(for_plot, aes(x = x, y = probs)) +
  geom_bar(stat = "identity") +
  ggtitle(label = "pmf of W when m = 20, n = 20", subtitle = "With super-imposed normal pdf") +
  stat_function(fun = ~dnorm(.x, 200, sqrt(m*n*(m + n + 1)/12)), color = "red")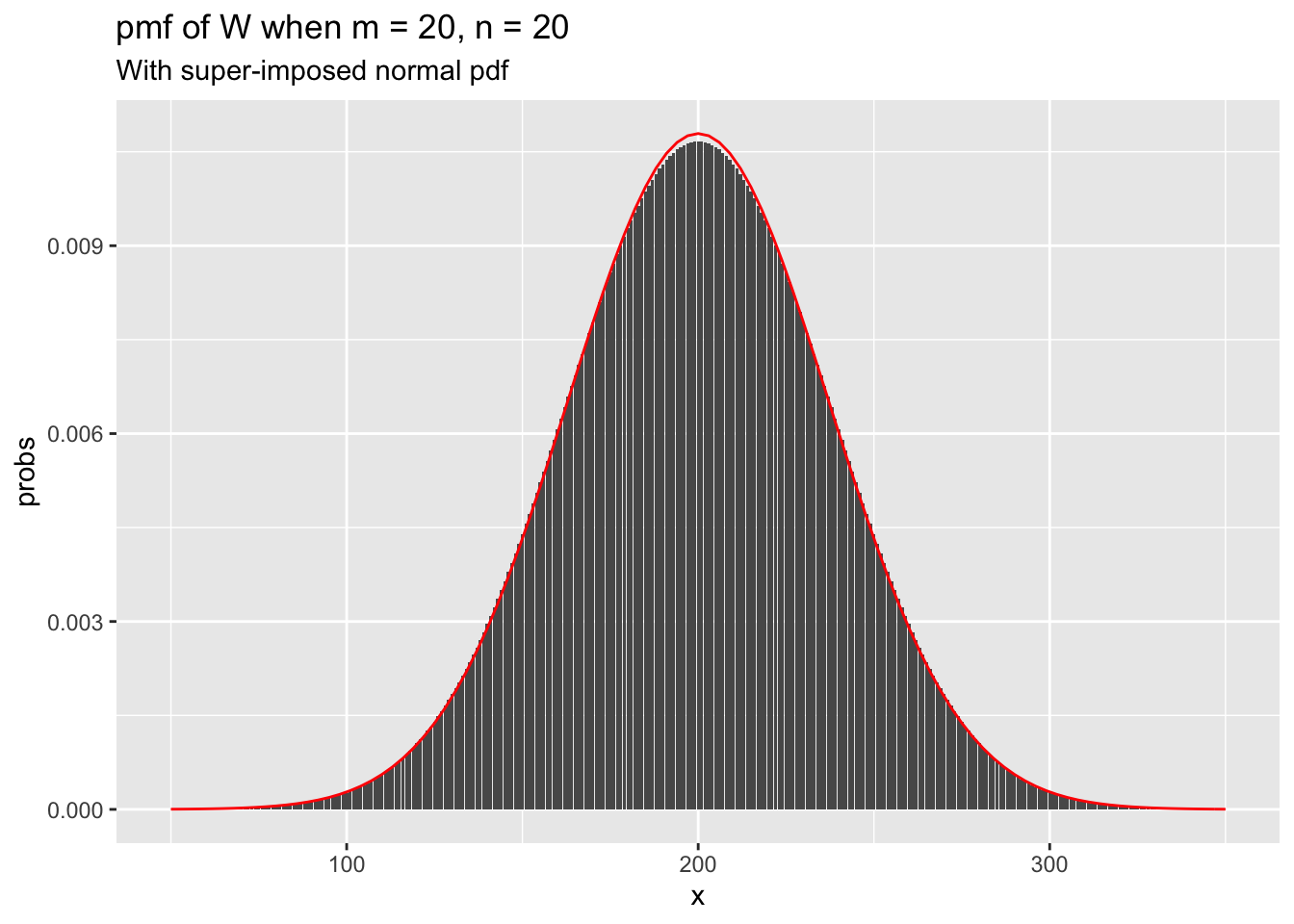

The function wilcox.test will compute test statistics and \(p\)-values in one simple step.

wilcox.test(c(5, 11), c(0, 3, 10))
## 
##  Wilcoxon rank sum exact test
## 
## data:  c(5, 11) and c(0, 3, 10)
## W = 5, p-value = 0.4
## alternative hypothesis: true location shift is not equal to 0

8.2.1 Example

Let’s look at an example from this paper22. Hillier et al. were interested in whether academic papers on climate change got more or fewer citations based on their narrative style. They assessed various aspects of the narrative style of the papers, and also counted the number of citations. The data set climate in the fosdata package summarizes their data for articles in three of the more prestigious journals.

Let’s load the data and do some exploring.

climate <- fosdata::climate

For the purposes of this example, we are going to look at whether the distribution of articles with an appeal in the abstract are associated with different citation rates than those without an appeal. An appeal being yes indicates that the author made an explicit appeal to the reader or a clear call for action. The normalized_citation variable gives the number of citations per year since publication. Let’s restrict to those two variables to clean things up a bit.

climate <- select(climate, binary_appeal, normalized_citations, abstract_number)
climate <- mutate(climate, binary_appeal = factor(binary_appeal, levels = 0:1, labels = c("No", "Yes")))
ggplot(climate, aes(x = binary_appeal, y = normalized_citations)) + 
  geom_boxplot(outlier.size = -1) +
  geom_jitter(height = 0, width = 0.2)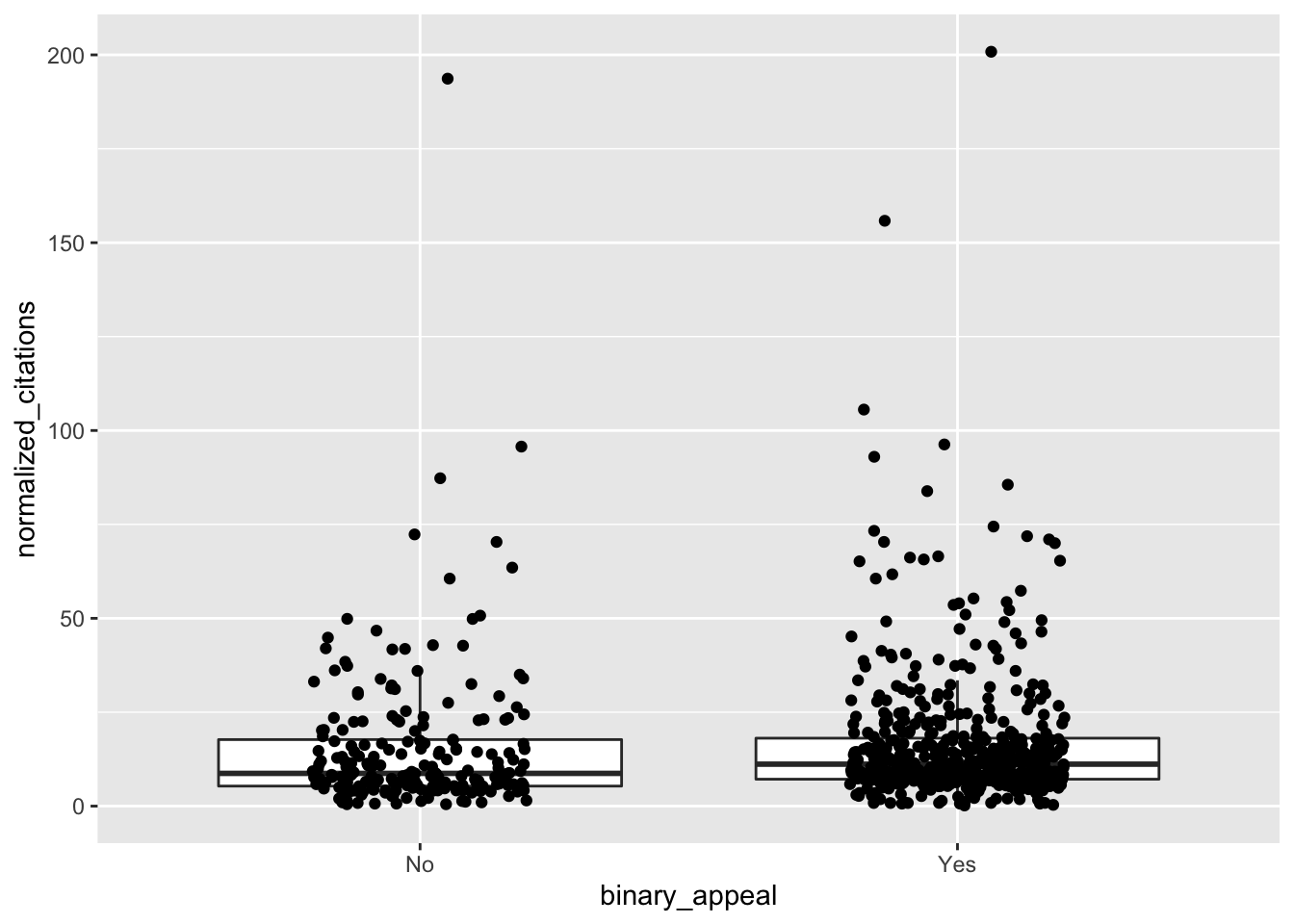

It’s a bit hard to see what is going on. Let’s compute some summary statistics.

climate %>% 
  group_by(binary_appeal) %>% 
  summarize(mean = mean(normalized_citations),
            sd = sd(normalized_citations), 
            skew = e1071::skewness(normalized_citations), 
            N = n())
## `summarise()` ungrouping output (override with `.groups` argument)
## # A tibble: 2 x 5
##   binary_appeal  mean    sd  skew     N
##   <fct>         <dbl> <dbl> <dbl> <int>
## 1 No             15.5  19.6  4.54   213
## 2 Yes            16.7  18.4  4.17   519

One thing that we notice is that there is quite a bit of skewness in these variables. The authors took the log of the citation variable, which lowered the skewness and made the data look more normal. A \(t\)-test without transforming the data would be problematic even with 200-500 samples because of the level of skewness of the data, as well as the outliers. Instead, we will use a Wilcoxon Rank Sum test to test

\(H_0\): the distribution of papers with an appeal is the same as the distribution of papers without an appeal.

\(H_a\): the distribution of papers with an appeal is different than the distribution of papers without an appeal.

wilcox.test(normalized_citations ~ binary_appeal, data = climate)
## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  normalized_citations by binary_appeal
## W = 47608, p-value = 0.003182
## alternative hypothesis: true location shift is not equal to 0

Note the use of ~ in wilcox.test; this is similar to its use in t.test, where we are telling R how we want to group the data. We reject the null hypothesis that the two distributions are the same at the \(\alpha = .05\) level.

Recall that the expected value of the test statistic is

213 * 519 /2
## [1] 55273.5

The test statistic that we obtained is 47608, which is lower than the expected value. This indicates that the no appeal papers are cited less frequently than would be expected under the null hypothesis.

In general, once we end up rejecting the null hypothesis, we will be interested in determining how the populations are different. One common, but restrictive, assumption is that the underlying populations are the same except for possibly a location shift. For example, we might assume that both populations are normal with standard deviation 1, but unknown mean. In this case, the only possible difference would be that one of the populations is probabilistically larger than the other population.

There are other instances, however, when there are different explanations for why \(H_0\) is rejected, and it can be challenging to determine exactly why \(H_0\) was rejected. Suppose for example, that population 1 consists of numbers uniformly distributed on \([-1, 1]\), and population 2 consists of numbers uniformly distributed on \([-2, -1]\) with probability \(1/2\), and numbers uniformly distributed on \([1,2]\) with probability \(1/2\). These distributions are different, but \(P(X > Y) = P(X < Y) = 1/2\). Let’s see what percentage of times, on average, we reject \(H_0\).

N <- 100
sim_data <- replicate(10000, {
  d1 <- runif(N, -1, 1)
  d2 <- sample(c(-2, 1), N, replace = TRUE) + runif(N)
  wilcox.test(d1, d2)$p.value
})
mean(sim_data < .05)
## [1] 0.0916

We see that the test rejects \(H_0\) more than with probability \(\alpha = .05\), but the test still has very low power. If we increase \(N\), we get the following table:

N <- c(10, 20, 50, 100, 200, 500, 1000)
power <- sapply(N, function(N) {
  sim_data <- replicate(1000, {
    d1 <- runif(N, -1, 1)
    d2 <- sample(c(-3, 2), N, replace = TRUE) + runif(N)
    wilcox.test(d1, d2)$p.value
  })
  mean(sim_data < .05)
})
data.frame(N = N, power = power) %>% 
  knitr::kable(digits = 4,
               caption = "Power of Wilcoxon test")
Table 8.3: Power of Wilcoxon test
N power
10 0.128
20 0.103
50 0.120
100 0.088
200 0.106
500 0.130
1000 0.102

We see that, as \(N \to \infty\), we do not have that the power of the test gets close to 1. It can be shown (see Section 8.5 for details) that when \(N \to \infty\), the power converges to about \(0.1095\). We say a test is consistent if the power converges to 1 as \(N \to \infty\).

Theorem 8.1 Suppose \(X\) and \(Y\) are random variables with finite variance and \(P(X > Y) \not= P(X < Y)\). Then, the Wilcoxon signed rank test is consistent. That is, as the number of samples goes to infinity, the power converges to 1.

In particular, we recommend using the Wilcoxon signed rank test when we suspect, or wish to detect, a difference in populations that is of the type \(P(X > Y) \not= P(X < Y)\).

8.2.2 Ordinal Data

Another common use of wilcox.test is when the data is ordinal rather than numeric. Ordinal data is such that given data points \(p_1\) and \(p_2\), we can determine whether \(p_1\) is bigger than \(p_2\), less than \(p_2\), or equal to \(p_2\). However, we do not necessarily have a natural way of assigning numbers to the data points. Many people do assume there is a way of assigning numbers to the ordinal categories, but that doesn’t necessarily mean that it is a correct thing to do. For more information, see the somewhat whimsical book Do not use means with Likert scales.

A typical example of ordinal data is Likert-scale data. We have all seen surveys where we are asked to perform tasks such as:

Circle the response that most accurately reflects your opinion

Question Strongly Agree Agree Neutral Disagree Strongly Disagree
Pride and Prejudice is a great book 1 2 3 4 5
wilcox.test is a useful R command 1 2 3 4 5

Although the options are listed as numbers, it does not necessarily make sense to treat the responses numerically. For example, if one respondent Strongly Disagrees that wilcox.test is useful, and another Strongly Agrees, is the mean of those responses Neutral? What is the mean of Strongly Agree and Agree? If the responses are numeric, what units do they have? So, it may not (and often does not) make sense to treat the responses to the survey as numeric data, even though it is encoded as numbers. However, we can order the responses in terms of amount of agreement as Strongly Agree > Agree > Disagree > Strongly Disagree. Note that I left out Neutral, because Neutral responses open a whole new can of worms. For example, we don’t know whether someone who put Neutral for Question (1) did so because they have never read Pride and Prejudice, or because they read it and don’t have an opinion on whether it is a great book. In one case, the response might better be treated as missing data, while in the other it would be natural to include the result between Agree and Disagree.

Example

Returning to the movieLens data, the number of stars that a movie receives as a rating can definitely be ordered from 5 stars being the most down to 1/2 star being the least. It is not as clear that the number of stars should be treated numerically, as it is more like asking whether a movie is Very Good, Good, OK, Bad or Very Bad. Consider the movies Toy Story and Toy Story II. Recall that the data that we have in our movie lens data set is a random sample from all users. Is there sufficient evidence to suggest that there is a difference in the ratings of Toy Story and Toy Story II in the full data set?

We need to think some about this question. Recall that the movies data set consists of observations pulled from 610 distinct users. It would not be realistic to think that if a person rates both Toy Story and Toy Story 2, that their ratings would be independent of one another. So, let’s recast the question as follows. Among those people who have only rated one or the other movie, is there sufficient evidence to suggest that there is a difference in the ratings of Toy Story and Toy Story II in the full data set?

We should also decide whether we want to do a one-sided or a two-sided test. Some people have strong opinions about which Toy Story movie is better, but I don’t believe we have sufficient evidence or reason to do a one-sided test. So, let \(X\) be the rating of Toy Story for a randomly sampled person in the large dataset who only rated one of the two movies. Let \(Y\) be the rating of Toy Story II for a randomly sampled person who only rated one of the two movies. Our null and alternative hypotheses are

\(H_0: X\) and \(Y\) have the same distribution \(H_a: X\) and \(Y\) do not have the same distribution, and we wish to detect whether one of the Toy Story’s is more likely to be rated higher than the other.

In order to do a two-sample Wilcoxon test, we need to load the data:

movies <- fosdata::movies

Now, we need to pull out the ratings that correspond to Toy Story and Toy Story II. We begin by finding the movieID of the Toy Story movies:

filter(movies, stringr::str_detect(title, "Toy Story")) %>% 
  select(movieId, title) %>% 
  distinct()
##   movieId              title
## 1       1   Toy Story (1995)
## 2    3114 Toy Story 2 (1999)
## 3   78499 Toy Story 3 (2010)

Next, we create a data frame that only has the ratings of the Toy Story movies in it, then filter out only those ratings from people who rated just one of the two movies.

ts <- filter(movies, movieId %in% c(1, 3114))
ts <- ts %>% group_by(userId) %>% 
  mutate(N = n()) %>% 
  filter(N == 1)

Now, we can perform the Wilcoxon test:

wilcox.test(rating ~ title, data = ts)
## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  rating by title
## W = 1060.5, p-value = 0.9448
## alternative hypothesis: true location shift is not equal to 0

And we can see that there is not a statistically significant difference in the ratings of Toy Story and Toy Story II, so we do not reject the null hypothesis.

8.2.3 Discussion

The primary benefit of using wilcox.test versus t.test is that the assumptions that we have made are weaker. For example, if your data is ordinal rather than numeric, it would not be appropriate to use a t-test without finding a statistically valid way of assigning the ordinal data to numerical values. However, the assumptions on wilcox.test are only that the data points can be compared to determine which is larger, so wilcox.test works just fine with ordinal data.

Wilcox.test in the two sample case is also more resistant to outliers than t.test, just as it is in the one-sample version. When your underlying data is normal, t.test will be more powerful. If your underlying data is not skewed, then typically at about 30 samples t.test works pretty well. When data is heavily skewed, you may need up to 100, 500 or even more samples before t.test is accurate. One down side of wilcox.test is that it is harder to interpret the alternative hypothesis; t.test has a nice, clean statement about the mean, while wilcox.test only concludes that the distributions are not equal.

When communicating your results to others, especially those who are not statistically sophisticated, it may be useful to include a common language effect size. One that we recommend is Vargha and Delaney’s \(A\). Roughly speaking (if there are no ties), Vargha and Delaney’s \(A\) reports the percent of time that samples from one population will be larger than samples from the other population. This effect size can be used in the context of t-tests, but is even more natural in the context of the rank based tests in this chapter. Let’s look at an example to see how it can be computed.

We compute the observed effect size by counting the number of times that samples from population one are larger than those in population two, plus one half the number of ties. We divide by the total number of comparisons to get a percentage of times that population one is greater than population two. Recalling how the test statistic was computed, this is simply the test statistic divided by the number of comparisons that are made. We consider ratings from the movies data set, and we compare the ratings for Sense and Sensibility (1995) to The Sixth Sense (1999). The corresponding MovieID’s for those movies are 17 and 2762. We again restrict to those raters who only rated one of the two movies.

sensible_movies <- movies %>% 
  filter(movieId %in% c(17, 2762))
sensible_movies <- sensible_movies %>% 
  group_by(userId) %>% 
  mutate(N = n()) %>% 
  filter(N == 1)
wilcox.test(rating ~ title, data = sensible_movies)
## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  rating by title
## W = 3089.5, p-value = 0.65
## alternative hypothesis: true location shift is not equal to 0

We get a \(p\)-value of .65. We compute the common language effect size two ways: once from the definition and once using the test statistic.

s_and_s_ratings <- filter(sensible_movies, movieId == 17) %>% 
  pull(rating)
t_s_s_ratings <- filter(sensible_movies, movieId == 2762) %>% 
  pull(rating)
sum(sapply(s_and_s_ratings, function(x) {
  sum(x > t_s_s_ratings) + 1/2 * sum(x == t_s_s_ratings)
}))/(length(s_and_s_ratings) * length(t_s_s_ratings))
## [1] 0.4776592
test_stat <- wilcox.test(rating ~ title, data = sensible_movies)$statistic
test_stat/(sum(sensible_movies$movieId == 17) * sum(sensible_movies$movieId == 2762))
##         W 
## 0.4776592

We see that Sense and Sensibility is preferred by about 47.8% of the raters, while The Sixth Sense is preferred by about 53.2% of the raters. (This is only formally true if we imagine that for those that are tied, the breakdown would be 50/50 if the rating scale were finer).

There is a package, effsize that has a built in function which will compute Vargha and Delaney’s \(A\) from the data with no manipulation. The call is:

effsize::VD.A(rating ~ title, data = sensible_movies)

You will, as usual, have to install the package effsize if you have not yet done so. This package also provides adjectives such as negligible, small, etc. associated with effect sizes. As with Cohen’s \(d\), these adjectives can be domain dependent so that a negligible effect size in one area might be considered a large effect size in another, so use these carefully. We also point out that the value that appears is roughly the percentage of people who prefer the movie that comes first when the grouping is cast as a factor. In this case, that is Sense and Sensibility.

Example

Let’s reconsider the Toy Story example. What if we want to compare the ratings from among those who have seen both movies? This is an example of a paired, one-sided Mann-Whitney-Wilcoxon test. We need to assume that the relative difference between ratings is meaningful. That is, we need to assume that a difference of 1 star is less than a difference of 1.5 stars, no matter what the actual star ratings are.

ts <- filter(movies, movieId %in% c(1, 3114))
ts <- ts %>% group_by(userId) %>% 
  mutate(N = n()) %>% 
  filter(N == 2)

It would be inappropriate to use a Wilcoxon rank sum test on this data, because the samples are not independent. We expect for there to be a correlation between the ratings of Toy Story and Toy Story 2. Therefore, we will used a paired test. This is equivalent to doing a Wilcoxon signed rank test on the differences between post and pre weights. In particular, the differences should satisfy the assumptions of the Wilcoxon signed rank test.

Let’s see if the differences are roughly symmetric.

ts %>% 
  select(title, rating, userId) %>% 
  tidyr::pivot_wider(names_from = title, values_from = rating) %>% 
  janitor::clean_names() %>% 
  mutate(diff = toy_story_1995 - toy_story_2_1999) %>% 
  select(diff) %>%
  with(hist(diff))
## Adding missing grouping variables: `user_id`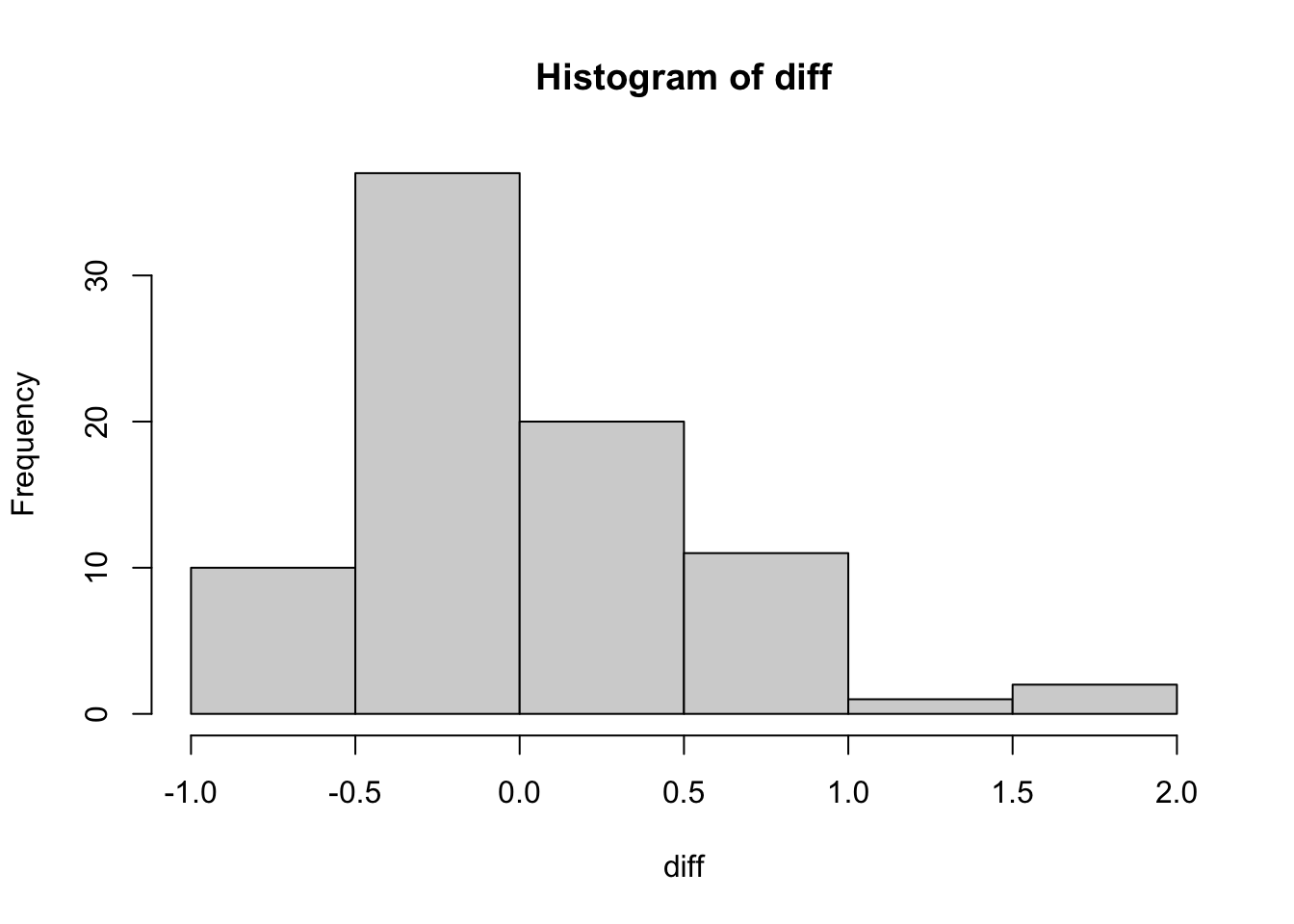

Hmmm. That might be a problem. It is a bit hard to say. The skewness of the differences through e1071::skewness is .311, so let’s proceed.

\(H_0\) the median difference in ratings is zero

\(H_a\): the median difference ratings is not zero.

wilcox.test(rating ~ title, data = ts, paired = TRUE)
## Warning in wilcox.test.default(x = c(4.5, 4, 3.5, 3, 4, 3, 5, 4, 2.5, 3, :
## cannot compute exact p-value with ties
## Warning in wilcox.test.default(x = c(4.5, 4, 3.5, 3, 4, 3, 5, 4, 2.5, 3, :
## cannot compute exact p-value with zeroes
## 
##  Wilcoxon signed rank test with continuity correction
## 
## data:  rating by title
## V = 742, p-value = 0.003114
## alternative hypothesis: true location shift is not equal to 0

With a \(p\)-value of 0.003, we would reject the null hypothesis at the \(\alpha = .05\) level and conclude there is a difference in median ratings. Note that if we hadn’t paired the data, we would have seen a much large \(p\)-value; in fact, we would have failed to reject at the \(\alpha = .05\) level.

#Not appropriate!
wilcox.test(rating ~ title, data = ts)
## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  rating by title
## W = 3783.5, p-value = 0.084
## alternative hypothesis: true location shift is not equal to 0

The choice to use a paired test is a decision that had a large influence on the outcome of the analysis. It is important to think carefully about your data before going too far in your analysis. If you start playing around with different analyses, looking for one that shows something is significant, then you can end up with drastically underestimated probabilities of Type I errors. Think about it like this - most every data set has something about it that doesn’t happen too often. If you keep testing until you land on whatever that is, then you have only learned something about the underlying process if your result is reproducible. That’s not to say you can’t look for trends in data; you just need to be sure the trend you find is representative of all data of this type, and can be replicated in further experiments. The more different kinds of analyses you perform before finding something that is significant, the more questionable your result becomes.

8.3 Simulations

We begin by comparing the power of Wilcoxon rank-sum test with t-test when the underlying data is normal. We assume we are testing \(H_0: \mu = 0\) versus \(H_a: \mu \not= 0\) at the \(\alpha = .05\) level, when the underlying population is truly normal with mean 1 and standard deviation 1 with a sample size of 10. Let’s first estimate the percentage of time that a t-test correctly rejects the null-hypothesis.

set.seed(1)
sum(replicate(10000, t.test(rnorm(10,1,1))$p.value < .05))
## [1] 7932

We see that we correctly reject \(H_0\) 79.3% of the time in this simulation Let’s see what would have happened had we used Wilcoxon.

sum(replicate(10000, wilcox.test(rnorm(10,1,1))$p.value < .05))
## [1] 7845

Here, we see that we correctly reject \(H_0\) 78.5% of the time in this simulation. If you repeat the simulations, you will see that indeed the t.test correctly rejects \(H_0\) more often than the Wilcoxon test does, on average.

However, if there is a departure from normality in the underlying data, Wilcoxon can outperform t.test. Let’s repeat the above simulations in the case that we are sampling from a t distribution with 3 degrees of freedom that has been shifted to the right by one.

sum(replicate(10000, t.test(rt(10,3) + 1)$p.value < .05))
## [1] 5358
sum(replicate(10000, wilcox.test(rt(10,3) + 1)$p.value < .05))
## [1] 5423

Here, we see that Wilcoxon outperforms t, but not by a tremendous amount.

Note that we didn’t explain how to compute the \(p\)-value when using two-sample Wilcoxon. One way we can do it is via simulation. Let’s return to the mtcars example from above, and recall that we are testing the displacement versus the transmission. Let’s remind ourselves how many data points we have:

nrow(mtcars)
## [1] 32
sum(mtcars$am == "1")
## [1] 13

We have 13 with manual transmission and 19 with automatic transmission. If there were really no difference in the displacement for automatic and manual transmissions, then the ranks of the displacement would be assigned randomly. To simulate that, we imagine that we have 32 possible ranks, and we sample 13 of them to form the ranks of displacements for the manual transmissions.

manualRanks <- sample(32, 13)

The automatic ranks are the ones that are not in manualRanks. It can be a little tricky to pull these out. Here are a couple of ways:

which(!(1:32 %in% manualRanks))
##  [1]  1  2  5  6  7 11 12 13 14 15 16 19 21 22 26 27 29 30 31
 (1:32)[-manualRanks]
##  [1]  1  2  5  6  7 11 12 13 14 15 16 19 21 22 26 27 29 30 31
setdiff(1:32, manualRanks)
##  [1]  1  2  5  6  7 11 12 13 14 15 16 19 21 22 26 27 29 30 31
autoRanks <- setdiff(1:32, manualRanks)

Now, we need to compute the test statistic for this ranking. The easiest way is to use wilcox.test and pull it out from there.

wilcox.test(manualRanks, autoRanks)$statistic
##   W 
## 130

If it is bigger than or equal to the observed value of 214 or less than or equal to 33 (which is the value equally far from the expected value of 13*19/2 = 123.5), then the test statistic would be in the smallest rejection region that contains our observed test statistic. The \(p\)-value is the probability of landing in this rejection region, so we estimate it.

mean(replicate(20000, { 
  manualRanks <- sample(32, 13)
  autoRanks <- setdiff(1:32, manualRanks)
  abs(wilcox.test(manualRanks, autoRanks)$statistic - 123.5) >= 90.5
}))
## [1] 6e-04

Simulating these low probability events is not going to be extremely accurate. but we can say that the probability of getting a result that strong against the null hypothesis by change is very low. If you run the above code several times, you will see that it is between .0002 and .0005; so our estimate for the \(p\)-value based on this would be that it is somewhere in that range of values. Note that this is different than what wilcox.test returns, in part because we did not take into account ties in our simulation.

Another option would be to take the 32 data points that we have, and randomly assign them to either auto or manual transmissions, and estimate the \(p\)-value this way. The code would look like this: I am suppressing warnings in wilcox.test so we don’t get warned about ties so much!

mean(replicate(20000, {
  manualSample <- sample(32, 13) 
  manualDisp <- mtcars$disp[manualSample]
  autoDisp <- mtcars$disp[setdiff(1:32, manualSample)]
  abs(suppressWarnings(wilcox.test(manualDisp, autoDisp)$statistic) - 123.5) >= 90.5
}))
## [1] 2e-04

The results are similar to the previous method.

8.4 Robustness, power, and sample size

We begin with a discussion of the robustness of the one and two sample Wilcoxon tests. Recall that for the one-sample test, we assumed that the underlying population was symmetric about its mean. This is an important assumption, as the following example shows. Suppose that the underlying population is exponential with mean 1. We take a sample size of 20 and estimate via simulation the effective type I error rate associated with a Wilcoxon ranked-sum test.

simdata <- replicate(10000, {
  dat <- rexp(20, 1)
  wilcox.test(dat, mu = 1)$p.value
})
mean(simdata < .05)
## [1] 0.1242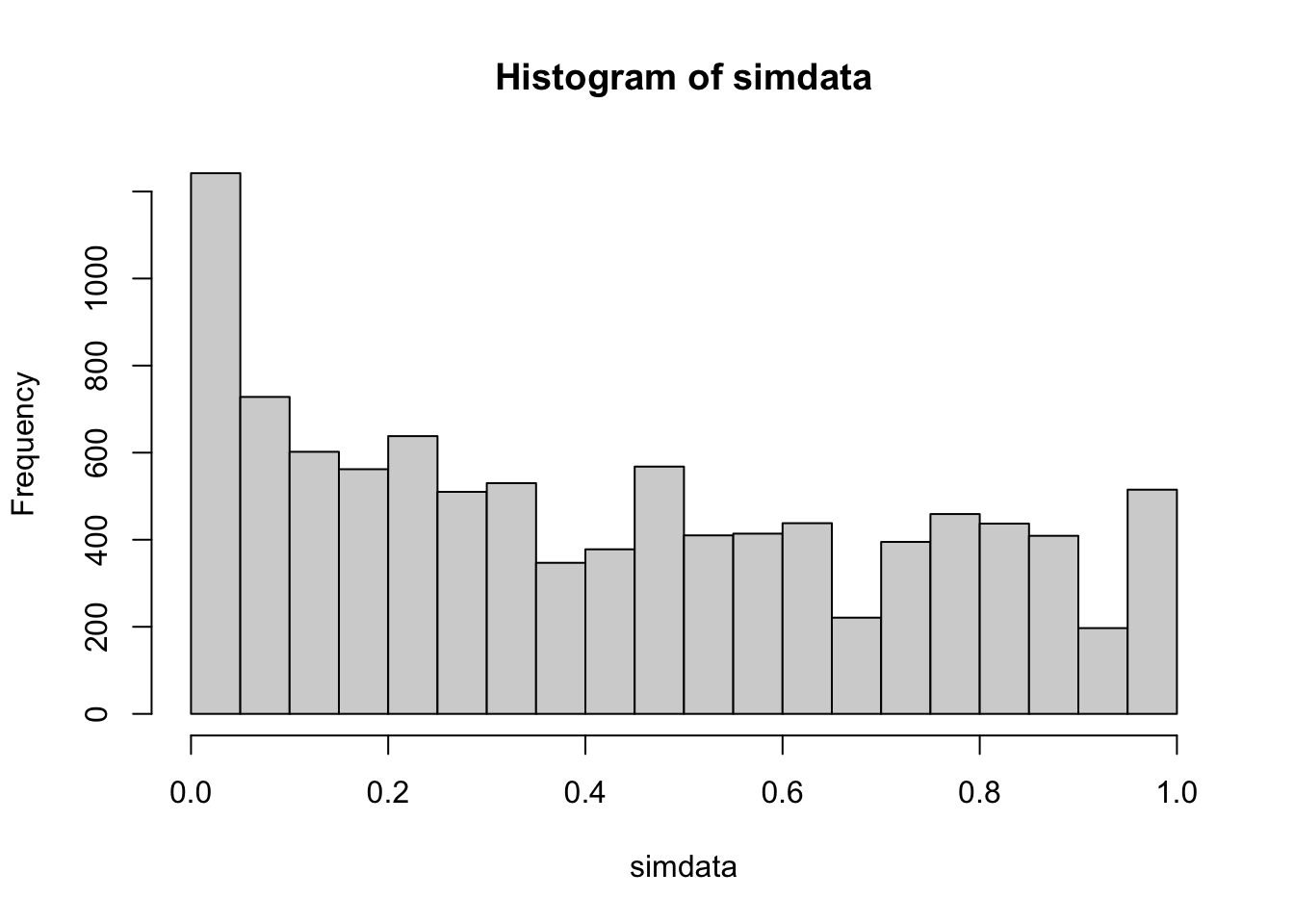
hist(simdata)

As we can see, there is a bias in \(p\)-values towards significance. The true effective type I error rate is more than twice the planned rate of 0.05. However, the Wilcoxon ranked sum test is robust to outliers.

simdata <- replicate(10000, {
  dat <- runif(20, -1, 1)
  dat[21] <- sample(c(-1,1), 1) * 100 #single large outlier
  wilcox.test(dat, mu = 0, alternative = "g")$p.value
})
hist(simdata)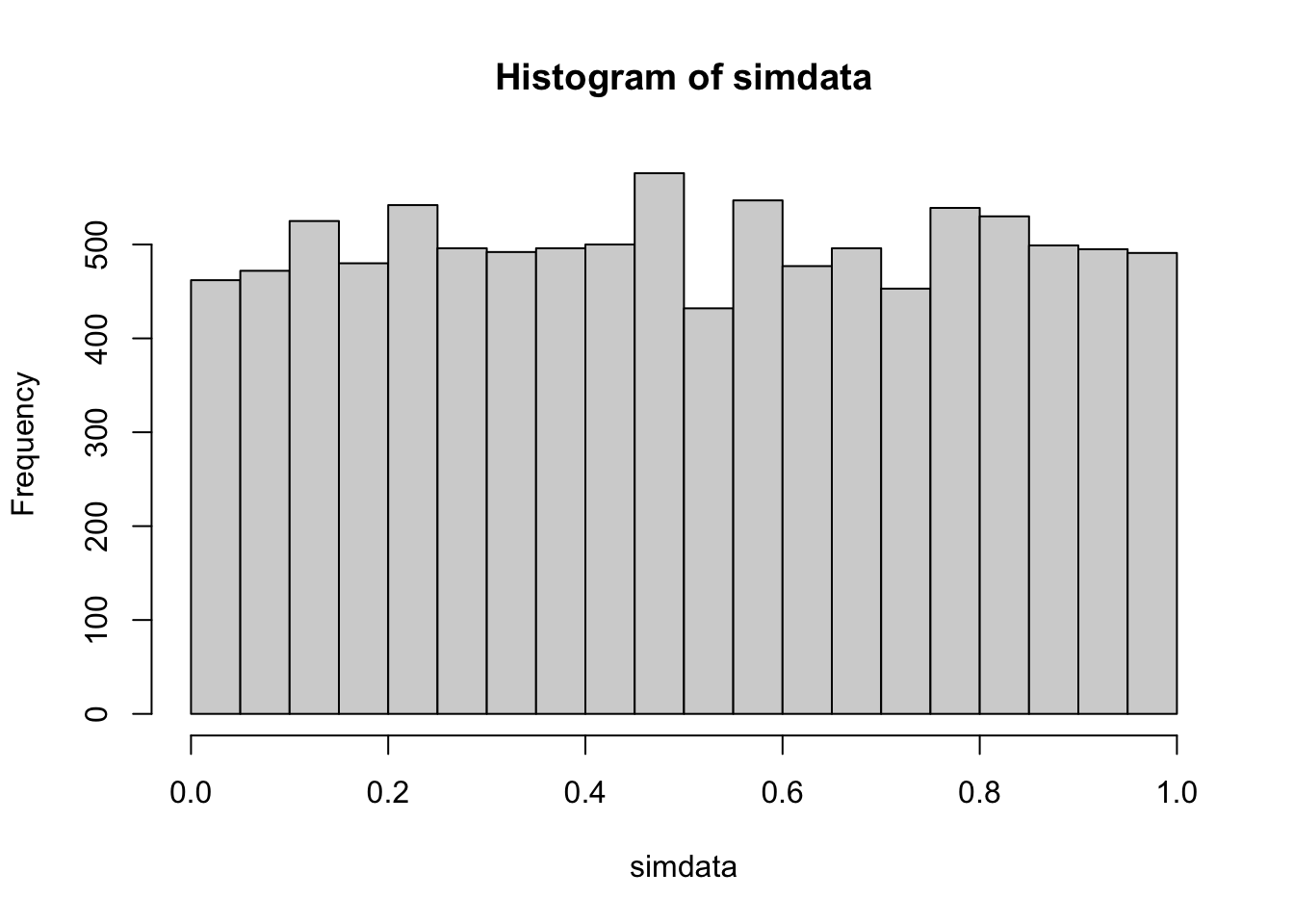

mean(simdata < .05)
## [1] 0.0462

We see that the type I error rate is slightly less than the planned rate of .05, but still reasonably close. The histogram of \(p\)-values is still reasonably close to the desired outcome of uniform on the interval \([0,1]\). We recall here that the type I error rate of a \(t\)-test in the above scenario is essentially 0, as is the power.

For the one-sample Wilcoxon test, in order to compute power we need to discuss the normal approximation method for estimating the \(p\)-value.

Next, we discuss robustness, power and sample size as it relates to the two-sample Wilcoxon test. Let’s begin by seeing that the two-sample test is not affected by skewness, at least in the instance when both populations are identical.

simdata <- replicate(10000, {
  dat1 <- rexp(20, 1)
  dat2 <- rexp(20, 1)
  wilcox.test(dat1, dat2)$p.value
})
hist(simdata)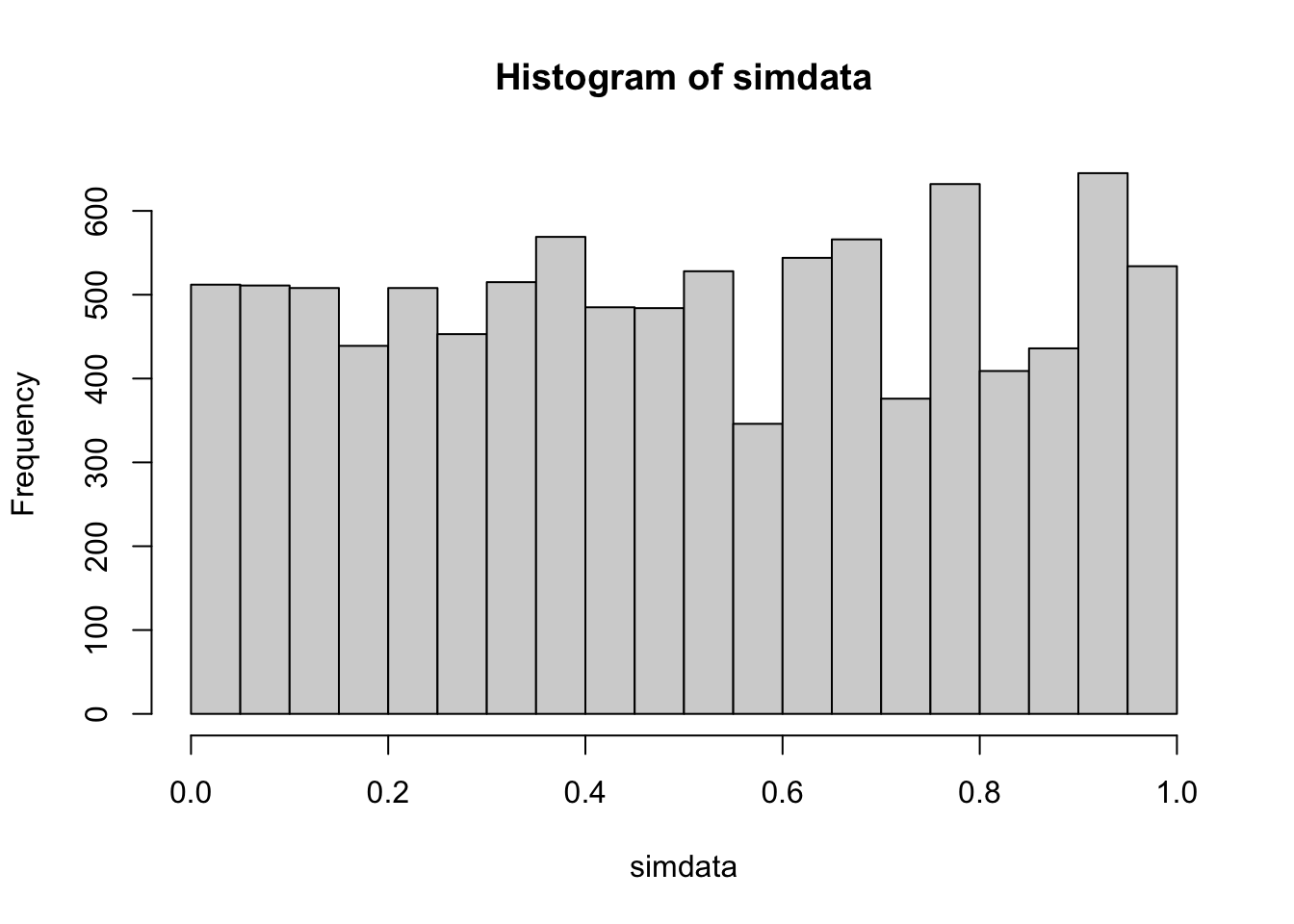

mean(simdata < .05)
## [1] 0.0512

Next, we imagine that we have a single large outlier in one of the two populations with a sample size of 20 in each population. We see that the two-sample test is robust to the influence of the outlier.

simdata <- replicate(10000, {
  dat1 <- runif(20, -1, 1)
  dat2 <- runif(20, -1, 1)
  dat1[21] <- sample(c(-1, 1), 1) * 100
  wilcox.test(dat1, dat2)$p.value
})
mean(simdata < .05)
## [1] 0.0467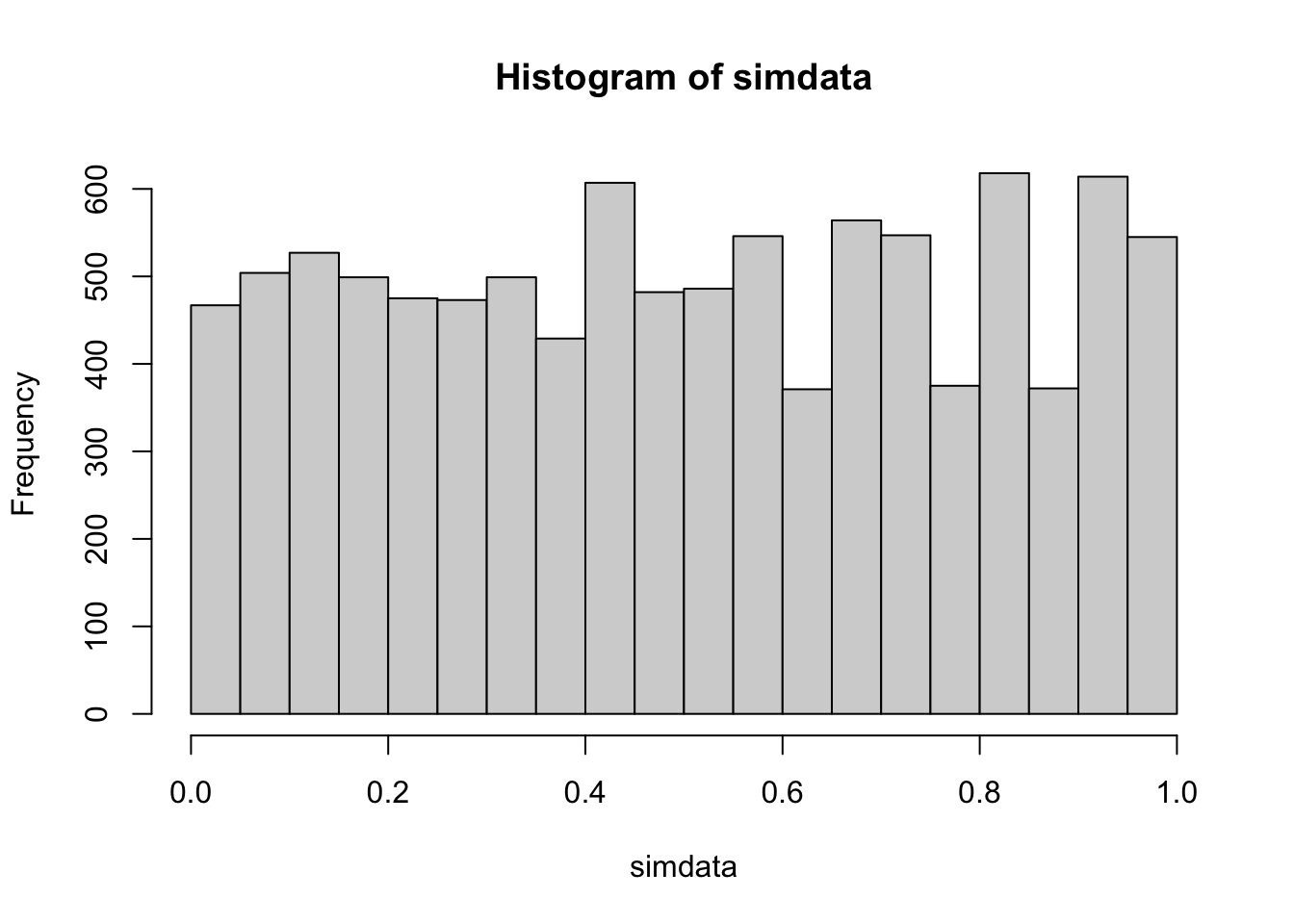
hist(simdata)

Note that if we just had an outlier of size 100 without a random sign, then the robustness of the test (especially when looking at one-sided tests) would change. We chose the random sign because in that situation, \(H_0\) is still true so we are checking whether the test is working as designed.

Recall that a type II error consists of failing to reject the null hypothesis when the alternative hypothesis is true, and the power of a test is the probability of rejecting the null when the alternative is true. When performing rank-based tests, we recommend using simulation to estimate power and sample sizes. In order to do so, we will need to know the \(\alpha\) level at which we wish to test and an estimate of the two populations. This can be challenging to do well.

Example Suppose we are designing an experiment in which students are randomly assigned to either a traditional classroom or a flipped classroom. At the end of the semester, students will be given a statement and asked whether they Strongly Agree, Agree, Disagree or Strongly Disagree with the statement, and we wish to determine whether there is a statistically significant difference in the responses between those in the traditional classroom and those in the flipped classroom. In order to have power of 80%, what number of students would need to be assigned to each group?

In order to do this, we estimate not only an effect size that we wish to detect, but also a specific distribution of responses in the two groups. After reading the literature, we decide that a reasonable effect would be probability distributions given in the table below.

Traditional Flipped
Strongly Agree 0.4 0.6
Agree 0.3 0.3
Disagree 0.1 0.1
Strongly Disagree 0.2 0.0

We recommend estimating the power for various sample sizes and plotting a smoothed version of the resulting line. When using this technique, we don’t need to estimate each probability as accurately as we would if we were only doing it once.

dd <- data.frame(p1 = c(.4, .3, .1, .2),
                 p2 = c(.6, .3, .1, 0))
sample_sizes <- seq(10, 150, length.out = 20)
powers <- sapply(sample_sizes, function(x) {
  tt <- replicate(500, {
    d1 <- sample(1:4, x, T, prob = dd$p1)
    d2 <- sample(1:4, x, T, prob = dd$p2)
    suppressWarnings(wilcox.test(d1, d2))$p.value
  })
  mean(tt < .05)
})
for_plot <- data.frame(sample_size = sample_sizes,
                       power = powers)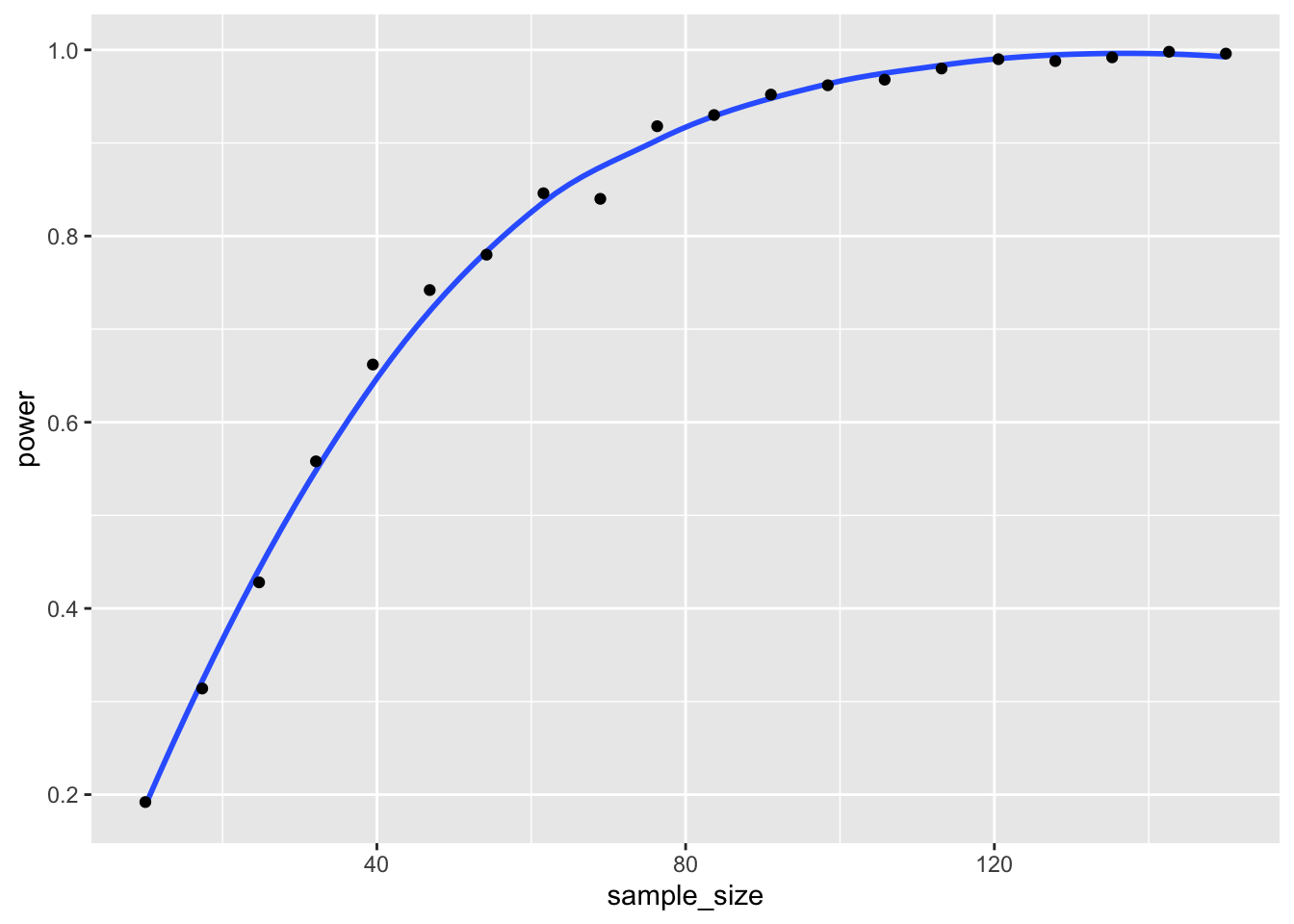
ggplot(for_plot, aes(x = sample_size, y = power)) +
  geom_smooth(se = F) + 
  geom_point()

We read off of the plot that in order to have a power of about 0.8, we would need about 58 samples in each group.

8.5 Consistency

In this section, we discuss the consistency of the one population t.test and the two population wilcox.test. A hypothesis test is said to be consistent if the probability of rejecting the null hypothesis given that the null hypothesis is false converges to 1 as the sample size goes to infinity. We will not be doing proofs of consistency for the tests that we have discussed, but we will examine this via simulations.

Consider t.test with one population, where we are testing \(H_0: \mu = \mu_0\) versus \(H_a: \mu \not= \mu_0\). We assume that the underlying population is normal with mean \(\mu_a \not= \mu_0\) and variance 1. We show through simulations that the probability of rejecting \(H_0\) gets close to 1 when the sample size gets very large.

We start by computing the percentage of times \(H_0\) will be rejected at the \(\alpha = .01\) level when \(\mu_0 = 1\), \(\mu_a = 2\) and the sample size is \(N = 20\).

mu0 <- 1
mua <- 2
sigma <- 1
N <- 20
pvals <- replicate(10000, {
  dat <- rnorm(N, mua, sigma)
  t.test(dat, mu = mu0)$p.value
})
mean(pvals < .01)
## [1] 0.9338

We see that with 20 samples, we already reject \(H_0\) about 93 percent of the time. We can recompute this for various values of \(N\) and \(\mu_a\) so that we can create some plots.

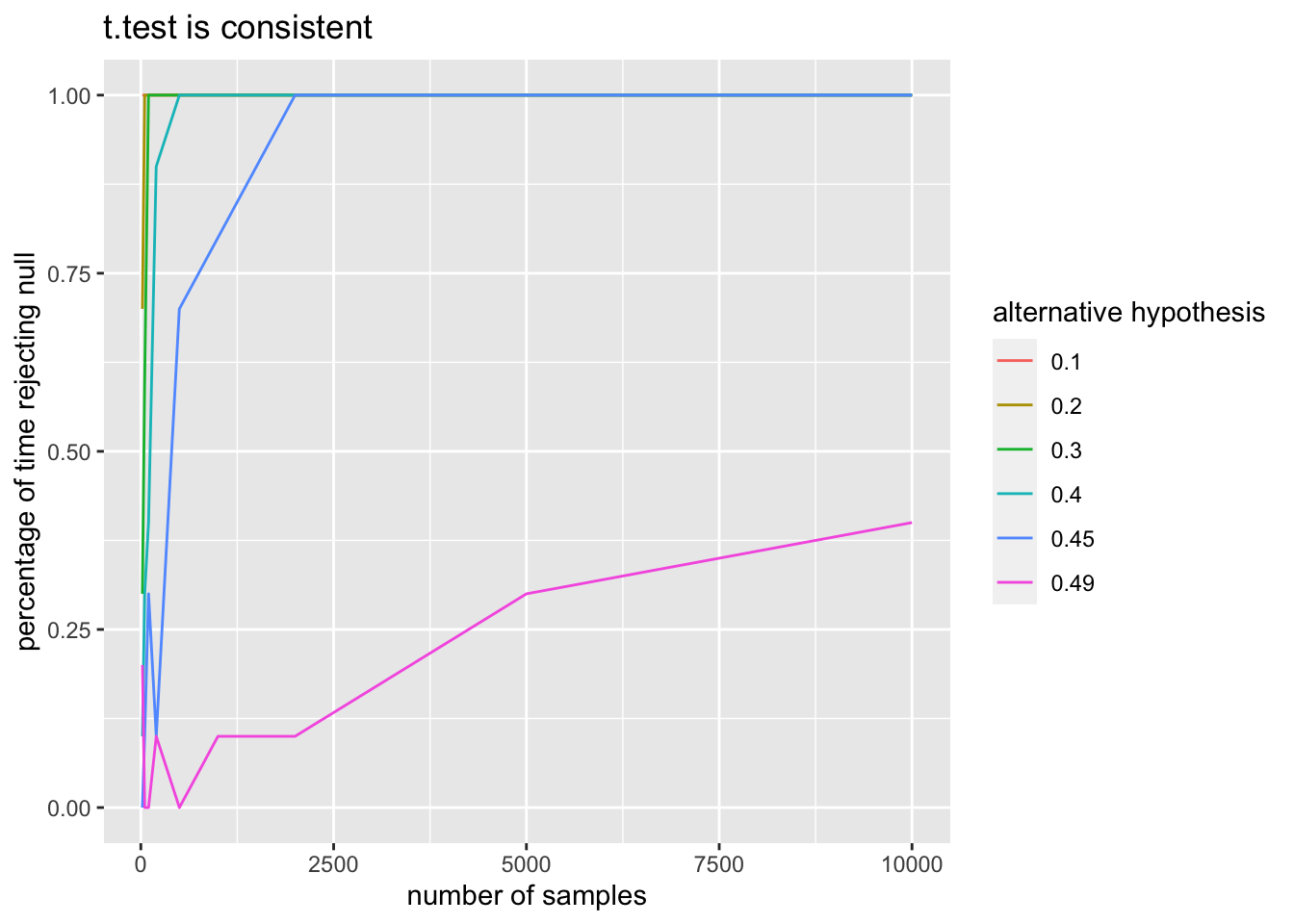
mua <- c(2, 1.5, 1.2, 1.1, 1.05, 1.02)
Ns <- c(20, 50, 100, 200, 500, 1000, 2000, 5000, 10000)
for_plot <- dplyr::bind_rows(lapply(mua, function(mua) {
  lapply(Ns, function(N) {
    pvals <- replicate(1000, {
      dat <- rnorm(N, mua, sigma)
      t.test(dat, mu = mu0)$p.value
    })
    data.frame(mua = mua,
         N = N,
         prob_reject = mean(pvals < .01)
    )
  })
}))
ggplot(for_plot, aes(x = N, y = prob_reject, color = factor(mua))) +
  geom_line() +
  labs(x = "number of samples", 
       y = "percentage of time rejecting null",
       color = "alternative hypothesis",
       title = "t.test is consistent")

As we can see from the plot, it appears that the probability of rejecting \(H_0\) is getting larger as the sample size increases, and it also appears to be converging to 1. We would need to take more samples to see this for \(\mu_a = 1.02\), but that is also a very small difference between the null and alternative hypothesis.

Now we repeat this for the Wilcoxon Rank Sum test. Recall that we said that this test is not always consistent, and we saw an example where it did not appear that the probability of rejecting the null hypothesis converged to 1. However, it is consistent when \(P(X > Y) \not= P(X < Y)\). To make things simple, we will assume that \(X\) is supported on \([1,2]\) and that \(Y\) takes values 0 and 3 with probabilities not equal to 1/2. The closer the probabilities are to 1/2, the more difficult samples we would probably need to consistently reject \(H_0\).

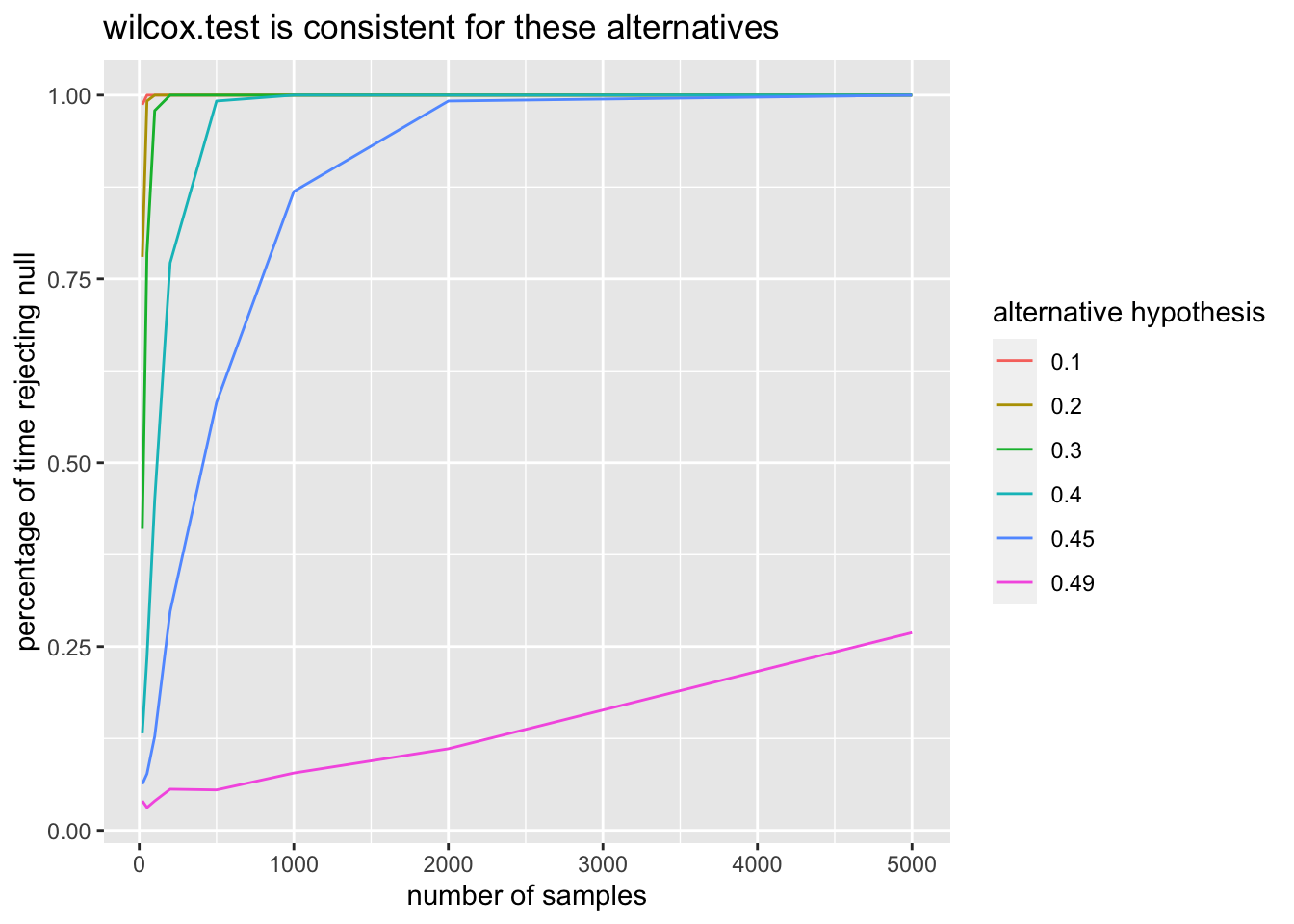
ps <- c(.1, .2, .3, .4, .45, .49)
Ns <- c(20, 50, 100, 200, 500, 1000, 2000, 5000)
for_plot_wilcox <- dplyr::bind_rows(lapply(ps, function(ps) {
  lapply(Ns, function(N) {
    x <- runif(N, 1, 2)
    pvals <- replicate(1000, {
      y <- sample(c(0, 3), size = N, replace = TRUE, prob = c(ps, 1 - ps))
      suppressWarnings(wilcox.test(x, y))$p.value
    })
    data.frame(mua = ps,
         N = N,
         prob_reject = mean(pvals < .01)
    )
  })
}))
ggplot(for_plot_wilcox, aes(x = N, y = prob_reject, color = factor(mua))) +
  geom_line() +
  labs(x = "number of samples", 
       y = "percentage of time rejecting null",
       color = "alternative hypothesis",
       title = "wilcox.test is consistent for these alternatives")

Again, we can see that the percentage of times rejected appears to be converging to 1 as the sample size goes to infinity.

8.6 Summary

In this section, we provided an alternative to t.test. In the one-sample case, we can use the Wilcoxon signed rank test when the population is symmetric and we have taken a random sample from it, and it is preferred over t.test when either the data is ordinal and means cannot be taken, or when in the presence of outliers. When the underlying population is normal, use t.test because it has slightly larger power. When the population is skew or unknown (but with no outliers), use t.test with the caveats regarding sample size presented in Chapter 7.

In the independent two-sample case, we can use the Wilcoxon rank sum test as an alternative to t.test. Use the Wilcoxon rank sum test when the data is ordinal, when there may be outliers, or when the sample sizes are small enough that the Central Limit Theorem may not apply. Recall that the sample size required for the Central Limit Theorem to apply depends on the distribution. Use t.test when the populations are normal or when the sample size is large enough that the Central Limit Theorem applies. If the data is ordinal, but can be transferred meaningfully to a numeric scale, then you can use t.test on the transferred data. However, it can be difficult to re-interpret your result in the original scale when you do this.

In the paired two-sample case, we can use the Wilcoxon signed rank test on the differences as an alternative to a t test on the differences. For the Wilcoxon signed rank test to be valid, the differences in values must be meaningful, and in particular, must satisfy the conditions of the Wilcoxon signed rank test. Use this when the data is ordinal with meaningful differences or when there are outliers.

Vignette: ROC Curves and the Wilcoxon Rank Sum Statistic

Suppose you wish to classify an object into one of two groups. It would be helpful if there were a variable \(X\) and a value \(x_0\) such that whenever \(X < x_0\) we would classify the object into group 1, and whenever \(X \ge x_0\) we would classify the object into group 2. A receiver operating charactersitc curve (ROC curve) is a graphical measurement of how well a variable discriminates between two alternatives.

As an example, let’s consider palmerpenguins::penguins and suppose that we are trying to distinguish between Adelie and Chinstrap penguins, based solely on bill length.

penguins <- palmerpenguins::penguins %>% 
  filter(species %in% c("Adelie", "Chinstrap")) %>% 
  mutate(species = droplevels(species))
ggplot(penguins, aes(x = bill_length_mm, y = flipper_length_mm, color = species)) + 
  geom_point() +
  geom_vline(xintercept = c(40.9, 46), linetype = "dashed")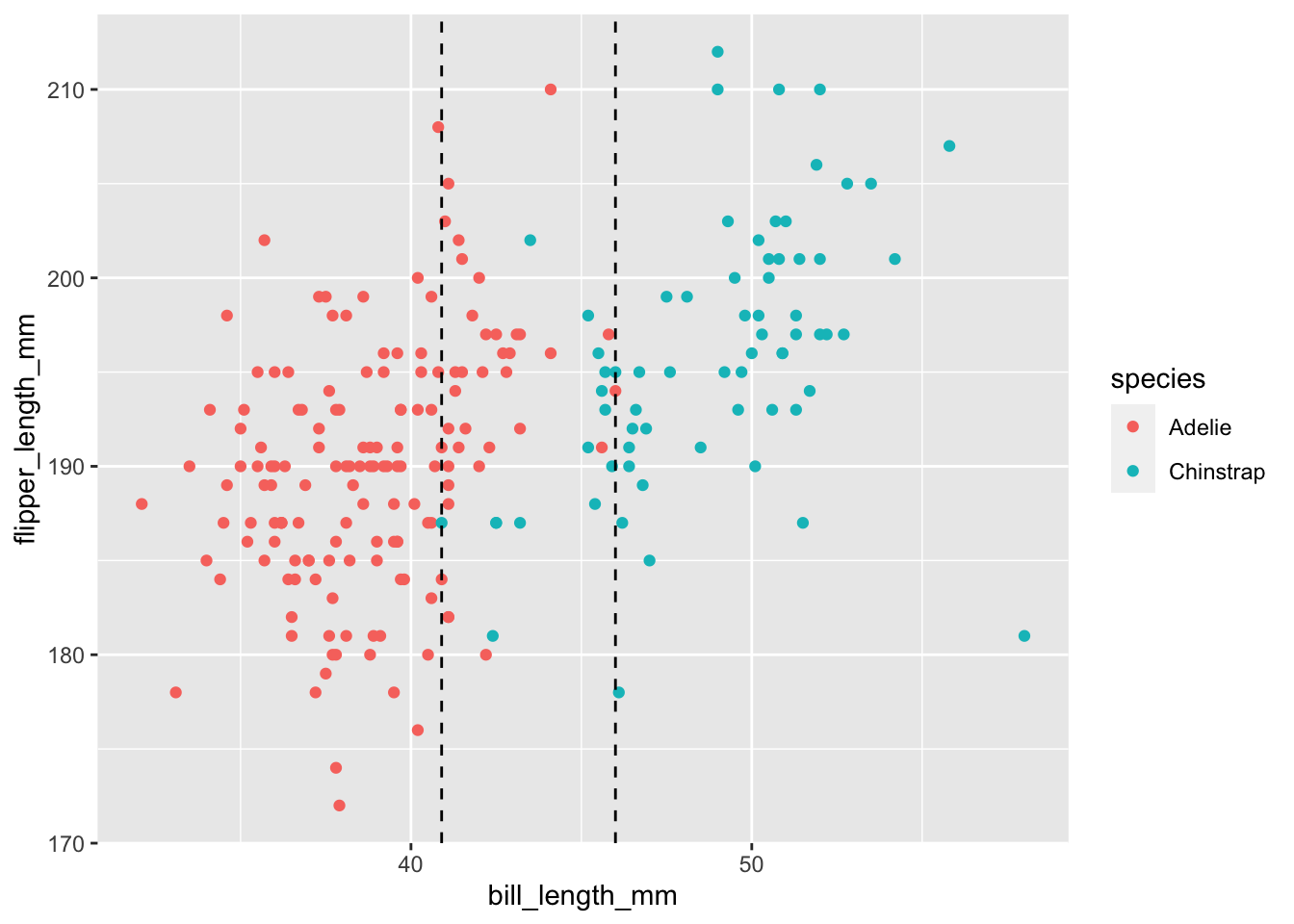

Based on this graph, we can see that there is not a value of bill length that completely separates the two variables. Whatever \(x_0\) we pick so that we assign and penguin with bill length less than \(x_0\) to be Adelie, we will be misclassifying some of the penguins. The ROC curve is computed as follows. Start at the smallest bill length and imagine that is your split value; all penguins with bill length less than that are classified as Adelie. The \(y\) coordinate is the percentage of penguins correctly classified as Adelie with that split value, and the \(x\) coordinate is the percentage of penguins incorrectly classified as Adelie with that split value. An ideal ROC curve would look like this:

dd <- data.frame(x = c(0, 0, 1), y = c(0, 1, 1)) 
ggplot(dd, aes(x = x, y  = y)) + 
  geom_line() +
  labs(title = "Ideal ROC Curve")

This means that there is at least one \(x_0\) such that all of the objects in group 1 have values less than \(x_0\) while all of the objects in group 2 have values at least \(x_0\). Let’s look at the ROC curve for the penguins using the ROCR package.

library(ROCR)
penguins <- select(penguins, species, bill_length_mm)
penguins <- penguins[complete.cases(penguins),]
pred <- prediction(penguins$bill_length_mm, penguins$species)
perf <- performance(pred, "tpr", "fpr")
plot(perf,colorize=TRUE)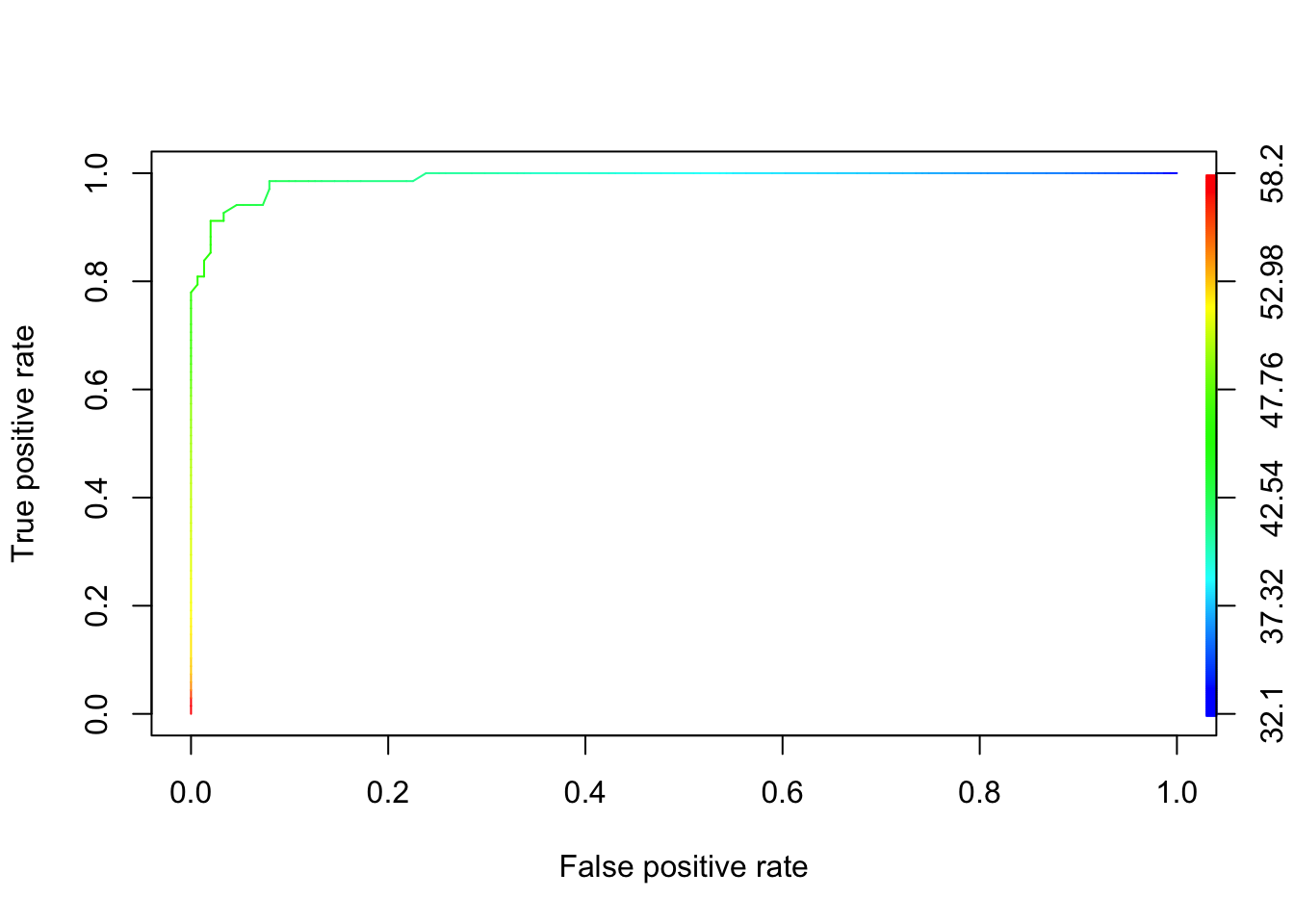

Note that the curve looks similar to the idealized version, except that it cuts off the corner at the top left. The curve there is green, which corresponds to bill lengths of around 45 mm. Those values of bills are exactly where we are unsure how the penguin should be classified.

The AUC or area under the ROC curve (think calculus area) is a measure of how separated the values are. The AUC measures the probability that a randomly selected member of group 2 has a higher value of the variable under question than a randomly selected member of group 1. It is used as a performance measure for machine learning algorithms.

With the background that we have developed, though, we can see it in terms of Vargha and Delaney’s \(A\), which is also the Wilcoxon Rank Sum test statistic divided by the total number of comparisons! So, now we have another way of conceptualizing Vargha and Delaney’s \(A\). It is the test statistic of a Wilcoxon Rank Sum test divided by the number of comparisons, or it is the area under ROC curve. The following code verifies that three ways of computing the AUC are the same in this context.

penguins <- mutate(penguins, species = factor(species, levels = c("Chinstrap", "Adelie")))
wilcox.test(bill_length_mm ~ species, data = penguins)$statistic/(151 * 68)
##         W 
## 0.9901636
effsize::VD.A(bill_length_mm ~ species, data = penguins)
## 
## Vargha and Delaney A
## 
## A estimate: 0.9901636 (large)
perf <- performance(pred, "auc")
perf@y.values[[1]]
## [1] 0.9901636

Exercises

  1. Consider the data in ex0221 in the Sleuth3 package. This data gives the Humerus length of 24 adult male sparrows that perished in a winter storm, as well as the Humerus length of 35 adult male sparrows that survived. The question under consideration is whether those that perished did so because of some physical characteristic; measured in this case by Humerus length.

    1. Create a boxplot of Humerus length for the sparrows that survived and those that perished. Note that there is one rather extreme outlier in the Perished group.
    2. Use a Wilcoxon ranked sum test to test whether the median Humerus length is the same in both groups.
    3. Is there evidence to conclude that the Humerus length is different in the two groups?

     

  2. Consider the sharks data in the fosdata package.23 Participants either watched a video or listened to an audio documentary about sharks while different types of music played. Participants were then asked to rate sharks on various dimensions such as gracefulness and viciousness. For this problem, consider only those participants who watched a video and head either ominous or uplifting music.

    1. Is there a difference in those participants’ responses to how vicious sharks are? Test at the \(\alpha = .05\) level.
    2. If there is a difference, provide the common language effect size and explain.

     

  3. Consider the data in ex0428 in the Sleuth3 package. This gives the plant heights in inches of plants of the same age, one of which was grown from a seed from a cross-fertilized flower, and the other of which was grown from a seed from a self-fertilized flower.

    1. Is there a significant difference in the height of the flowers at the \(\alpha = .05\) level?
    2. Create a boxplot of the height of the flowers for each type of fertilization. Comment on any abnormalities apparent. (Hint: this data is in “wide” format rather than “long” format, and you may want to use pivot_longer to convert it.)

     

  4. The data set malaria from the ISwR package contains 100 observations of children in Ghana. The data records each child’s age, levels of a particular antibody, and whether or not they have malaria symptoms.

    1. State and carry out a hypothesis test that the antibody levels (ab) differ between the groups with and without malaria symptoms. Use the Wilcoxon rank-sum test.
    2. Inspect a histogram of the ab variable. Would you use this variable in a t-test? Explain.
    3. Inspect a histogram of \(\log(\text{ab})\). Would you use this variable in a t-test? Explain.
    4. Carry out a t-test that the log of antibody levels differ between malaria groups and compare your results to the Wilcoxon test.

     

  5. The file flint.csv on the book webpage contains data on lead in tap water from Flint, Michigan in 2015 (Source: Flint Water Study). Is there a difference in the mean lead level after running water for 45 seconds (Pb2) and for 2 minutes (Pb3)?

    1. Use a paired t-test. Report your P-value and whether it is significant at the 0.05 level.
    2. Plot the data. Do you trust the results of your t-test in part a?
    3. Transform the data by computing the logarithm of the lead levels and try the t-test again.
    4. Test again using a Wilcoxon signed rank test.
    5. What is your overall conclusion and why?

     

  6. Assume that \(x_1,\ldots,x_n\) is a random sample from a symmetric distribution with mean 0.

    1. Show that the expected value of the Wilcoxon test statistic \(V\) is \(\displaystyle E(V) = \frac{n(n+1)}{4}\)
    2. Find \(\displaystyle \lim_{x_n\to \infty} E[V]\), which is the scenario of a single, arbitrarily large outlier.

     

  7. This problem explores the effective type I error rate for a one sample Wilcoxon and t-tests. Choose a sample of 21 values where \(X_1,\ldots,X_{20}\) are iid normal with mean 0 and sd 1, and \(X_{21}\) is 10 or -10 with equal probability. Test \(H_0: m = 0\) versus \(H_a: m\not= 0\) at the \(\alpha = .05\) level. How often does the Wilcoxon test reject \(H_0\)? Compare with the effective type I error rate for a t-test of the same data. Which test is performing closer to how it was designed?

  8. Compare the effective power of t.test versus wilcox.test in the case of testing \(H_0: \mu = 0\) versus \(H_a: \mu \not= 0\) when the underlying population is uniform with on the interval \([-0.5, 1]\), and the sample size is 30.

  9. This exercise explores how the Wilcoxon test changes when data values are transformed.

    1. Suppose you wish to test \(H_0: \mu = 0\) versus \(H_a: \mu \not = 0\) using a Wilcoxon test You collect data \(x_1 = -1,x_2 = 2,x_3 = -3,x_4 = -4\) and \(x_5 = 5\). What is the \(p\)-value?
    2. Now, suppose you multiply everything by 2: \(H_0: \mu = 0\) versus \(H_a: \mu\not = 0\) and your data is \(x_1 = -2,x_2 = 4,x_3 = -6,x_4 = -8\) and \(x_5 = 10\). What happens to the \(p\)-value? (Try to answer this without using R. Check your answer using R, if you must.)
    3. Now, suppose you square the magnitudes of everything. \(H_0: \mu = 0\) versus \(H_a: \mu \not= 0\), and your data is \(x_1 = -1,x_2 = 4,x_3 = -9,x_4 = -16\) and \(x_5 = 25\). What happens to the \(p\)-value?
    4. Compare your answers to the those that you got when you did the same exercise for \(t\)-tests in Exercise 7.8.

     

  10. Consider the movies data set.

    1. Is there sufficient evidence at the \(\alpha = .05\) level to conclude that people prefer one of the movies “Sleepless in Seattle” or “While you were Sleeping” to the other?
    2. Report Vargha and Delaney’s \(A\) effect size for this data, and interpret.

     

  11. Suppose you wish to test \(H_0:\mu = 3\) versus \(H_a: \mu\not= 3\). You collect the data points \(x_1 = -1\), \(x_2 = 0\), \(x_3 = 2\) and \(x_4 = 8\). Go through all of the steps of a Wilcoxon signed rank test and determine a \(p\)-value. Check your answer using R.

  12. In this problem, we estimate the probability of a type II error. Suppose you wish to test \(H_0:\mu = 1\) versus \(H_a: \mu\not=1\) at the \(\alpha = .05\) level.

    1. Suppose the true underlying population is \(t\) with 3 degrees of freedom, and you take a sample of size 20.
      1. What is the true mean of the underlying population?
      2. What type of error would be possible to make in this context, type I or type II? In the problems below, if the error is impossible to make in this context, the probability would be zero.
    2. Approximate the probability of a type I error if you use a t test.
    3. Approximate the probability of a type I error if you use a Wilcoxon test.
    4. Approximate the probability of a type II error if you use a t test.
    5. Approximate the probability of a type II error if you use a Wilcoxon test.
    6. Note that \(t\) random variables with small degrees of freedom have heavy tails and contain data points that look like outliers. Does it appear that Wilcoxon or t test is more powerful with this type of population?

     

  13. How well can hypothesis tests detect a small change? Suppose the population is normal with mean \(\mu = 0.1\) and standard deviation \(\sigma = 1\). We test the hypothesis \(H_0: \mu = 0\) versus \(H_a: \mu \neq 0\).

    1. When \(n = 100\), what percent of the time does a t-test correctly reject \(H_0\)?
    2. When \(n = 100\), what percent of the time does a Wilcoxon test correctly reject \(H_0\)?
    3. Repeat parts a and b with \(n = 1000\).
    4. The assumptions for both tests are satisfied, since the population is normal. Which test does a better job of rejecting the null hypothesis?

  1. Hillier A, Kelly RP, Klinger T (2016) Narrative Style Influences Citation Frequency in Climate Change Science. PLoS ONE 11(12): e0167983.↩︎

  2. Nosal AP, Keenan EA, Hastings PA, Gneezy A (2016) The Effect of Background Music in Shark Documentaries on Viewers’ Perceptions of Sharks. PLoS ONE 11(8): e0159279.↩︎