Chapter 10 Simple Linear Regression

Assume you have data that is given in the form of ordered pairs \((x_1, y_1),\ldots, (x_n, y_n)\). In this chapter, we study the model \(y_i = \beta_0 + \beta_1 x_i + \epsilon_i\), where \(\epsilon_i\) are iid normal random variables with mean 0. We develop methods for estimating \(\beta_0\) and \(\beta_1\), we examine whether the model is satisfied, we study prediction and confidence intervals for \(y\), and we perform inference on the slope and intercept.

10.1 Fitting a line

10.1.1 An introductory example

Consider the data Formaldehyde, which is built in to R:

Formaldehyde

##   carb optden
## 1  0.1  0.086
## 2  0.3  0.269
## 3  0.5  0.446
## 4  0.6  0.538
## 5  0.7  0.626
## 6  0.9  0.782

In this experiment, a container of the carbohydrate Formaldehyde of known concentration carb was tested for its optical density optden (a measure of how much light passes through the liquid). The variable carb is called the explanatory variable, denoted in formulas by \(x\). The optden variable is the response variable \(y\). In this data, the experimenters selected the values \(x_1 = 0.1\), \(x_2 = 0.3\), \(x_3 = 0.5\), \(x_4 = 0.6\), \(x_5 = 0.7\), and \(x_6 = 0.9\) and created solutions at those concentrations. They then measured the values \(y_1 = 0.086, \dotsc, y_6 = 0.782\).

A plot of this data shows a nearly linear relationship between the concentration of formaldehyde and the optical density of the solution:

Formaldehyde %>% 
  ggplot(aes(x = carb, y = optden)) + 
  geom_point()

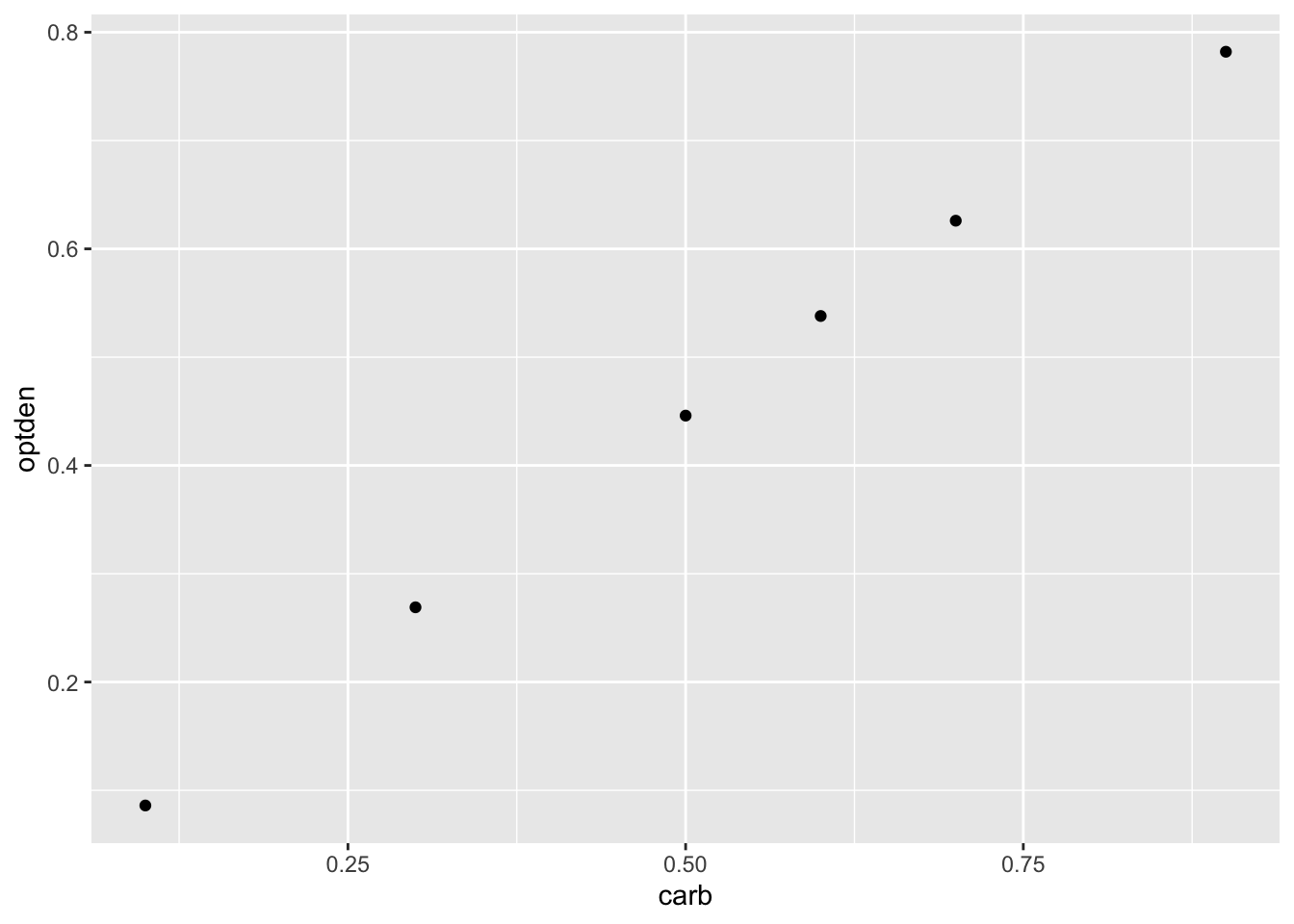
The goal of simple linear regression is to find a line that fits the data. The resulting line is called the regression line or the best fit line. R calculates this line with the lm command, which stands for linear model:

lm(optden ~ carb, data=Formaldehyde)

## 
## Call:
## lm(formula = optden ~ carb, data = Formaldehyde)
## 
## Coefficients:
## (Intercept)         carb  
##    0.005086     0.876286

In the lm command, the first argument is a formula. Read the tilde character as “explained by”, so that the formula says that optden is explained by carb. The output gives the coefficients of a linear equation \[ \widehat{\text{optden}} = 0.0050806 + 0.876286\cdot \text{carb}.\] The ggplot geom geom_abline can plot a line given an intercept and slope. Here is the data again, shown with the regression line:

Formaldehyde %>% ggplot(aes(x = carb, y = optden)) +
  geom_point() +
  geom_abline(intercept = 0.005086, slope = 0.876286)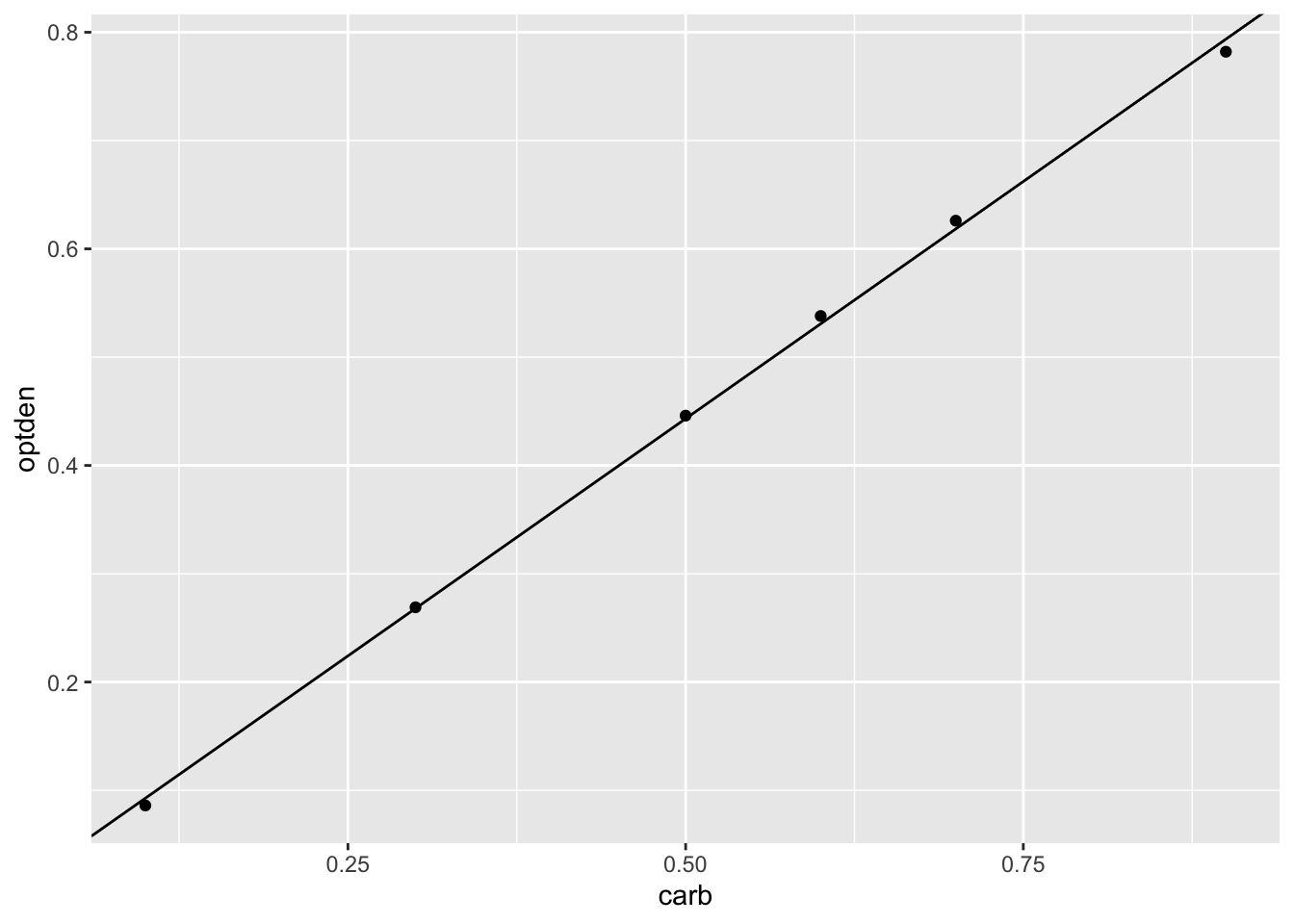

10.1.2 Least squares

Assume data comes in the form of ordered pairs \((x_1, y_1),\ldots,(x_n, y_n)\). Values of the slope \(\beta_1\) and the intercept \(\beta_0\) describe a line \(y = \beta_0 + \beta_1 x\).

The true values of the intercept and slope are denoted by \(\beta_0\) and \(\beta_1\). We will denote estimates of \(\beta_0\) and \(\beta_1\) based on data by \(\hat \beta_0\) and \(\hat \beta_1\). More generally, putting a hat on a variable indicates that we are talking about its estimate from the data. For each value of \(x_i\), the estimated regression line has value \(\hat y_i\) given by the linear equation: \[ \hat y_i = \hat \beta_0 + \hat \beta_1 x_i. \] The error associated with the estimation is \(\hat \epsilon_i = y_i - \hat y_i\). This error, \(\hat \epsilon_i\), is the vertical distance between the actual value of the data \(y_i\) and the value estimated by our line. (We will explain why \(\hat \epsilon\) has a hat below.)

The goal of regression is to choose \(\beta_0\) and \(\beta_1\) to make the error terms \(\hat \epsilon_i\) as small as possible.

Definition 10.1 The regression line for points \((x_1, y_1),\ldots,(x_n, y_n)\) is the line \[ y = \hat \beta_0 + \hat \beta_1 x \] which minimizes the sum of squared errors \[ SSE(\beta_0,\beta_1) = \sum_i \hat \epsilon_i^2 = \sum_i \left(y_i - (\beta_0 + \beta_1 x_i)\right)^2 \]

Note that in the previous equation, \(\beta_0\) and \(\beta_1\) are not the fixed unknown constants that determine the true relationship between \(x\) and \(y\), but rather variables that can take on any values. This is a common abuse of notation.

The sum of squared errors is not the only possible way to measure the quality of fit, so sometimes the line is called the least squares regression line. Minimizing SSE is reasonably simple, it involves all data points, and it is a smooth function (unlike, say, absolute value). Using SSE also has a natural geometric interpretation: minimizing SSE is equivalent to minimizing the length of the error vector \((\hat \epsilon_1,\dotsc,\hat \epsilon_n)\).

For the regression line, the error terms \(\hat \epsilon_i\) are called residuals. The lm command in R returns a data structure which contains the residuals as a variable.

Example Find \(\hat \beta_i\) for the Formaldehyde data, and calculate the residuals and the SSE.

In the notation developed above, the estimated intercept \(\hat \beta_0 = 0.005086\) and the estimated slope \(\hat \beta_1 = 0.876286\)

Formaldehyde_model <- lm(optden ~ carb, data = Formaldehyde)
Formaldehyde_model$residuals

##            1            2            3            4            5            6 
## -0.006714286  0.001028571  0.002771429  0.007142857  0.007514286 -0.011742857

sum(Formaldehyde_model$residuals ^ 2)

## [1] 0.0002992

In this code, the result of the lm function is stored in a variable we chose to call Formaldehyde_model. Observe that the first and sixth residuals are negative, since the data points at \(x_1 = 0.1\) and \(x_6 = 0.9\) are both below the regression line. The other residuals are positive since those data points lie above the line. The SSE for this line is 0.0002992.

If we fit any different line the SSE will be larger than 0.0002992. For example, using the line \(\widehat{\text{optden}} = 0 + 0.9\cdot \text{carb}\) results in a SSE of 0.0008, so it is not the best fit:

optden_hat <- 0.9 * Formaldehyde$carb  # fit values
optden_hat - Formaldehyde$optden  # compute errors

## [1] 0.004 0.001 0.004 0.002 0.004 0.028

sum( ( optden_hat - Formaldehyde$optden )^2 )  # compute SSE

## [1] 0.000837

10.2 Regression and predictions

Linear models are used to describe a relationship between variables and also to make predictions. This section explains how to interpret the regression line and make predictions with confidence.

Artwork by @allison_horst

The main example used in this section will be the dataset penguins from the palmerpenguins package. This has measurements of three species of penguins found in Antarctica, and was originally collected by Gorman et. al. in 2007-2009. For now, we focus on the Chinstrap species, and investigate the relationship between flipper length and body mass.

Here is a plot, using flipper length as the explanatory variable and body mass as the response. The geometry geom_smooth can fit various lines and curves to a plot. Here method = "lm" indicates that we want to use a linear model, the regression line.

library(palmerpenguins)
chinstrap <- filter(penguins, species == "Chinstrap")
chinstrap %>%
  ggplot(aes(x = flipper_length_mm, y = body_mass_g)) +
  geom_point() +
  geom_smooth(method = "lm") +
  labs(title = "Chinstrap penguins")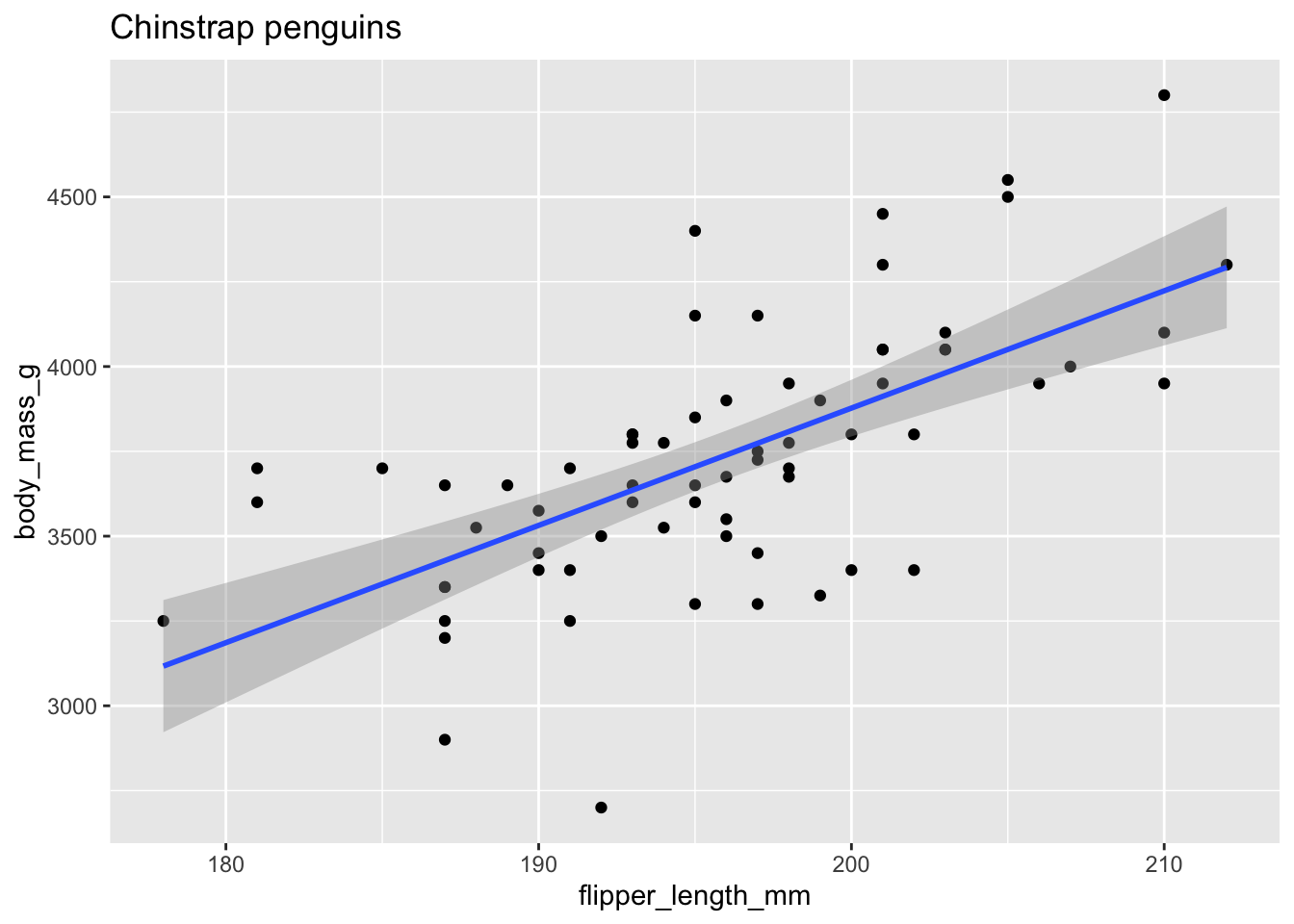

The upward slope of the line suggests that chinstrap penguins with longer flippers will have greater body mass. Here are the linear model and the coefficients of the regression line:

chinstrap_model <- lm(body_mass_g ~ flipper_length_mm, data = chinstrap)
chinstrap_model$coefficients

##       (Intercept) flipper_length_mm 
##       -3037.19577          34.57339

The equation of the regression line is \[ \widehat{\text{mass}} = -3037.19577 + 34.57339 \cdot \text{flipper length}. \] The estimated slope \(\hat \beta_1 \approx 34.6\) means that for every additional millimeter of flipper length, we expect an additional 34.6g of body mass. The estimated intercept \(\hat \beta_0 \approx -3037\) has little meaning, because it describes the supposed mass of a penguin with flipper length zero. This is typical: the slope of the regression line often has a useful interpretation while the intercept often does not.

Observe that ggplot includes a gray band around the regression line. This is the 95% confidence band for the regression line. Because the sample of penguins was random, the line resulting from regression analysis is random. Repeating the study would produce new measurements and a new line. So, the regression line shown is only an estimate of a hypothetical true regression line for the entire population. We are 95% confident that the true regression line lies within the gray band shown in the plot. We will explore this idea more in Section 10.7 with simulations.

Example

The data set child_tasks is available in the fosdata package and can be loaded into R via.

child_tasks <- fosdata::child_tasks

It contains results from a study³¹ in which 68 children were tested at a variety of executive function tasks. The variable stt_cv_trail_b_secs measures the speed at which the child can complete a “connect the dots” task called the Shape Trail Test, which you may try yourself on the sample image.

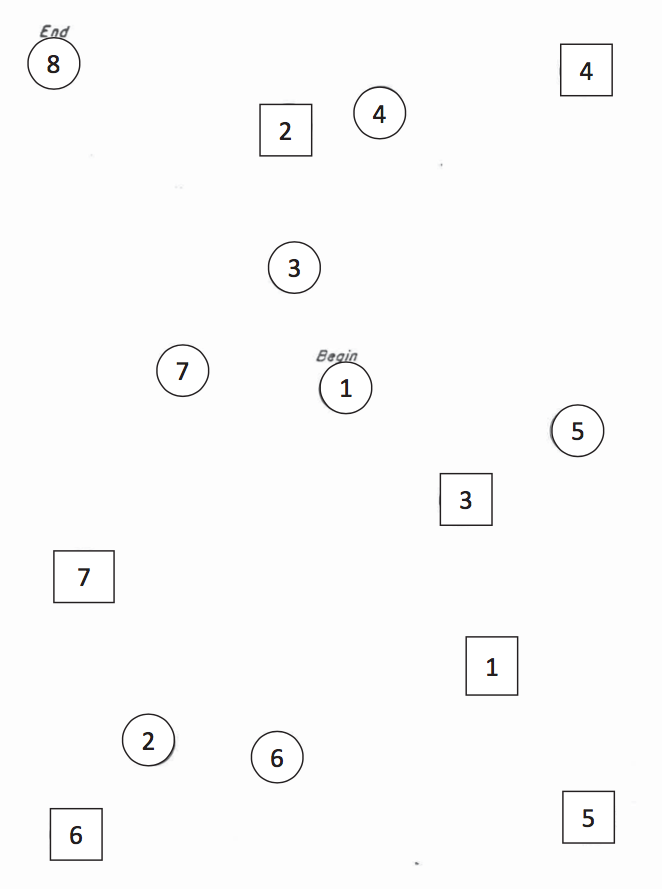
Figure 10.1: STT Trail B. Connect the circles in order.

How does a child’s age affect their speed at completing the Shape Trail Test? We choose age_in_months as the explanatory variable and stt_cv_trail_b_secs as the response variable.

child_tasks <- read.csv("data/child_tasks.csv")
child_tasks %>% ggplot(aes(x=age_in_months, y = stt_cv_trail_b_secs)) +
  geom_point() +
  geom_smooth(method = "lm")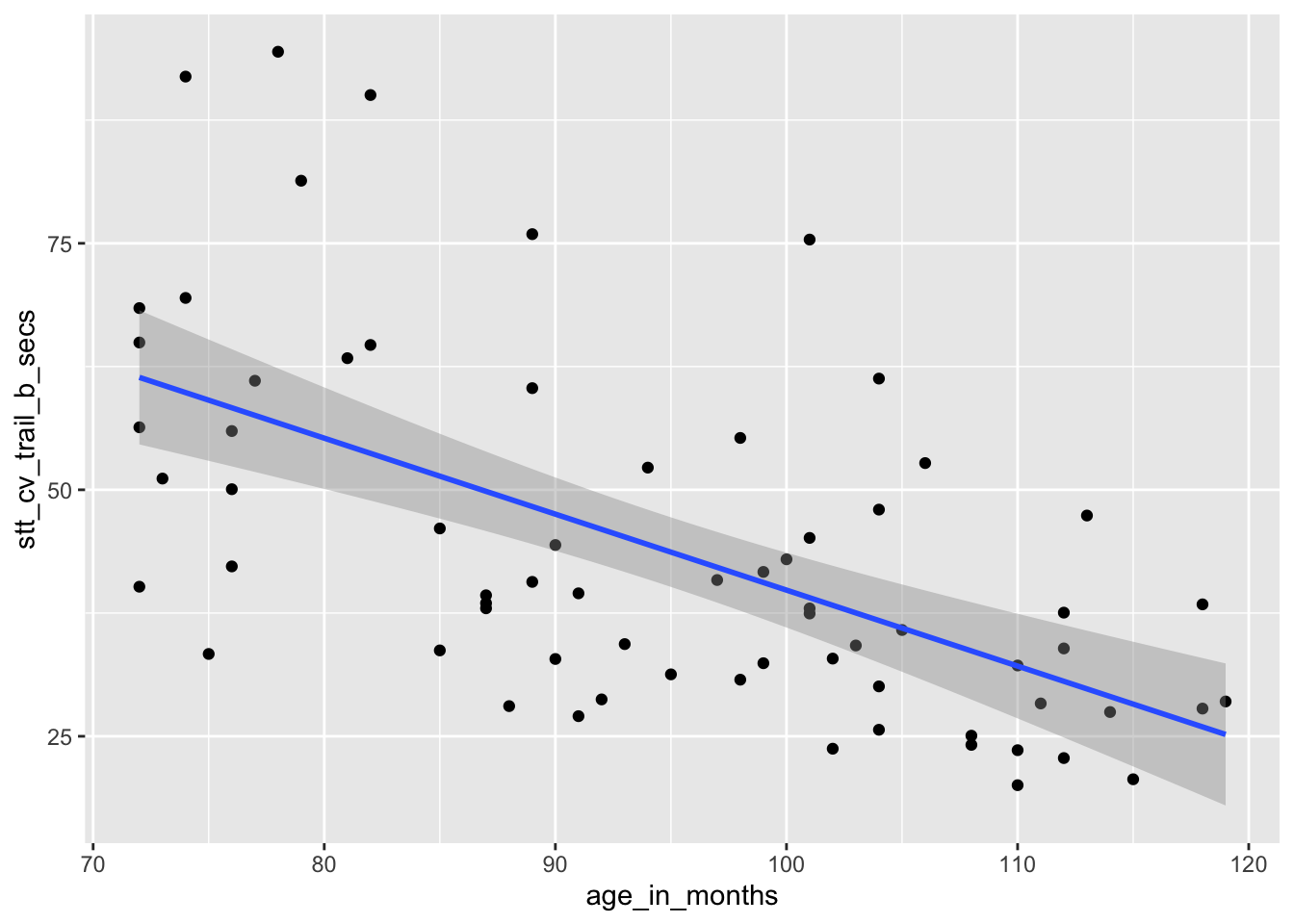

stt_model <- lm(stt_cv_trail_b_secs ~ age_in_months, data = child_tasks)
stt_model$coefficients

##   (Intercept) age_in_months 
##   116.8865146    -0.7706084

The regression line is given by the equation \[ \widehat{\text{test time}} = 116.9 - 0.77 \cdot \text{age} \]

The estimated slope \(\hat \beta_1 = -0.77\) indicates that each additional month of age reduces the mean time for children to complete the STT by 0.77 seconds on average. The estimated intercept \(\hat \beta_0 = 116.9\) is meaningless since it corresponds to a child of age 0, and a newborn child cannot connect dots.

10.2.1 Predictions

Suppose we have found the line of best fit given the data, and it is represented by \(y = \hat \beta_0 + \hat \beta_1 x\). We would like to be able to predict what happens if we collect new data, possibly at \(x\) values that weren’t in the original sample. Notationally, we will call \(x_\star\) the new \(x\) value. The value \(y_\star\) is the true mean value of \(y\) when \(x = x_\star\). We will denote \(\hat y_\star\) as a prediction of the response variable for a given value of the explanatory variable \(x\).

Our model \(Y = \beta_0 + \beta_1 x + \epsilon\) assumes that \(\epsilon\) is normal with mean zero, so that values of \(Y\) for a given \(x_\star\) will be normally distributed around the true mean value of \(y\) at \(x_\star\), namely \(\beta_0 + \beta_1 x_\star\). The prediction is a point estimate for the mean of the response variable at \(x_\star\).

Example Suppose you want to predict the body mass of a Chinstrap penguin whose flipper length is known to be 204mm. From the regression line, \[ \widehat{\text{mass}} = -3037.196 + 34.574 \cdot 204 = 4015.9 \] which predicts a body mass of 4015.9g.

The predict command in R can perform the same computation, given the model and a data frame containing the \(x\) values you wish to use to make predictions. Needing to wrap the explanatory variable in a data frame is a nuisance for making simple predictions, but will prove essential when using more complicated regression models.

predict(chinstrap_model, data.frame(flipper_length_mm = 204))

##        1 
## 4015.777

A key assumption in the linear model is that the error terms \(\epsilon_i\) are iid, so that they have the same variance for every choice of \(x_i\). This allows estimation of the common variance from the data, and from that an interval estimate for \(Y\). The predict command can provide a prediction interval using the interval option.³² By default, this option produces a prediction interval that includes 95% of all \(Y\) values for the given \(x\):

Example

predict(chinstrap_model, data.frame(flipper_length_mm = 204), interval = "predict")

##        fit      lwr      upr
## 1 4015.777 3412.629 4618.925

The fit column is the prediction, lwr and upr describe the prediction interval. We expect that 95% of new observations of chinstrap penguins with flipper length 204mm will have body weights between 3413 and 4619g.

Remark The choice of explanatory and response variable determines the regression line, and that choice is not reversible. We saw that a 204mm flipper predicts a 4016g body mass. Now switch the explanatory and response variables so that we can use body mass to predict flipper length:

reverse_model <- lm(flipper_length_mm ~ body_mass_g, data = chinstrap)
predict(reverse_model, data.frame(body_mass_g = 4015.777))

##       1 
## 199.189

A 4016g body mass predicts a 199mm flipper length, shorter than the 204mm you might have expected. In turn, a 199mm flipper length predicts a body mass of 3849g. Extreme values of flipper length predict extreme values of body mass, but the predicted body mass is relatively closer to the mean body mass. Similarly, extreme values of body mass predict extreme values of flipper length, but the predicted flipper length will be relatively closer to the mean flipper length. This phenomenon is referred to as regression to the mean.

Example How quickly will 95% of seven year old children complete the Shape Trail Test trail B?

predict(stt_model, data.frame(age_in_months = 7*12), interval = "predict")

##        fit      lwr      upr
## 1 52.15541 22.72335 81.58747

The prediction interval is \([22.7, 81.6]\) so that 95% of seven year old children will complete trail B between 22.7 and 81.6 seconds.

Remark Making predictions for \(x\) values that are outside the observed range is called extrapolation, and is not supported by statistical theory. In the child task study, the youngest children observed were six years old and the oldest were ten. Predictions about children outside of this age range would need to be treated with caution. For example, the regression line predicts that a 13 year old child would complete trail B in negative three seconds, clearly impossible.

10.2.2 Confidence intervals

The value \(\hat{y}_\star\) is the point estimate for the mean of the random variable \(Y\), given \(x_\star\). There are two sources of error in the point estimate. First, there is uncertainty in the estimates of \(\beta_0\) and \(\beta_1\). Second, there is random noise in the model itself. Like all point estimates, a confidence interval can give more refined information about the quality of the estimate.

For example, suppose you need to transport a chorus line of 80 chinstrap penguins, carefully selected to all have flipper length 204mm. The average weight for such a penguin is 4016g, so you expect your squad to weigh 321280 or about 321kg. How much will that total mass vary? Looking at the ggplot graph of chinstrap penguins above, the value 4016g comes from the regression line at \(x_\star=204\). That value varies by the width of the gray band above \(x_\star = 204\). The predict function can compute the range precisely:

predict(chinstrap_model, data.frame(flipper_length_mm = 204), interval = "confidence")

##        fit      lwr     upr
## 1 4015.777 3905.903 4125.65

This gives a 95% confidence interval of \([3906,4126]\) for the average mass of chinstrap penguins with flipper length 204mm. Assuming that the mean of the 80 penguins is approximately the same as the true mean of all penguins of that weight, we can multiply by 80 and then be 95% confident that the 20 penguin dance troupe will weigh between 312.4kg and 330kg.

To summarize this section, let’s plot the chinstrap penguin data again. This is a complicated plot, and it begins by building a new data frame called bounds_data which contains flipper length values from 178 to 212 and both confidence and prediction bounds for each of those \(x\) values. Here we go.

flipper_range = data.frame(flipper_length_mm = seq(178,212,2))

prediction_bounds <- predict(chinstrap_model, newdata = flipper_range, interval = "p")
colnames(prediction_bounds) <- c("p_fit","p_lwr","p_upr")
confidence_bounds <- predict(chinstrap_model, newdata = flipper_range, interval = "c")
colnames(confidence_bounds) <- c("c_fit","c_lwr","c_upr")

bounds_data <- cbind(flipper_range, confidence_bounds, prediction_bounds)

chin_plot <- chinstrap %>% ggplot(aes(x = flipper_length_mm, y = body_mass_g)) + 
  geom_point() + 
  geom_smooth(method = "lm") +
  labs(title="Chinstrap penguin flipper length and body mass",
       subtitle="Confidence bounds (dashed) and prediction intervals (orange)")

chin_plot <- chin_plot +
  geom_line(data = bounds_data, aes(y = c_lwr), linetype = "dashed") +
  geom_line(data = bounds_data, aes(y = c_upr), linetype = "dashed") 

chin_plot <- chin_plot +
  geom_line(data = bounds_data, aes(y = p_lwr), color="orange") +
  geom_line(data = bounds_data, aes(y = p_upr), color="orange")

chin_plot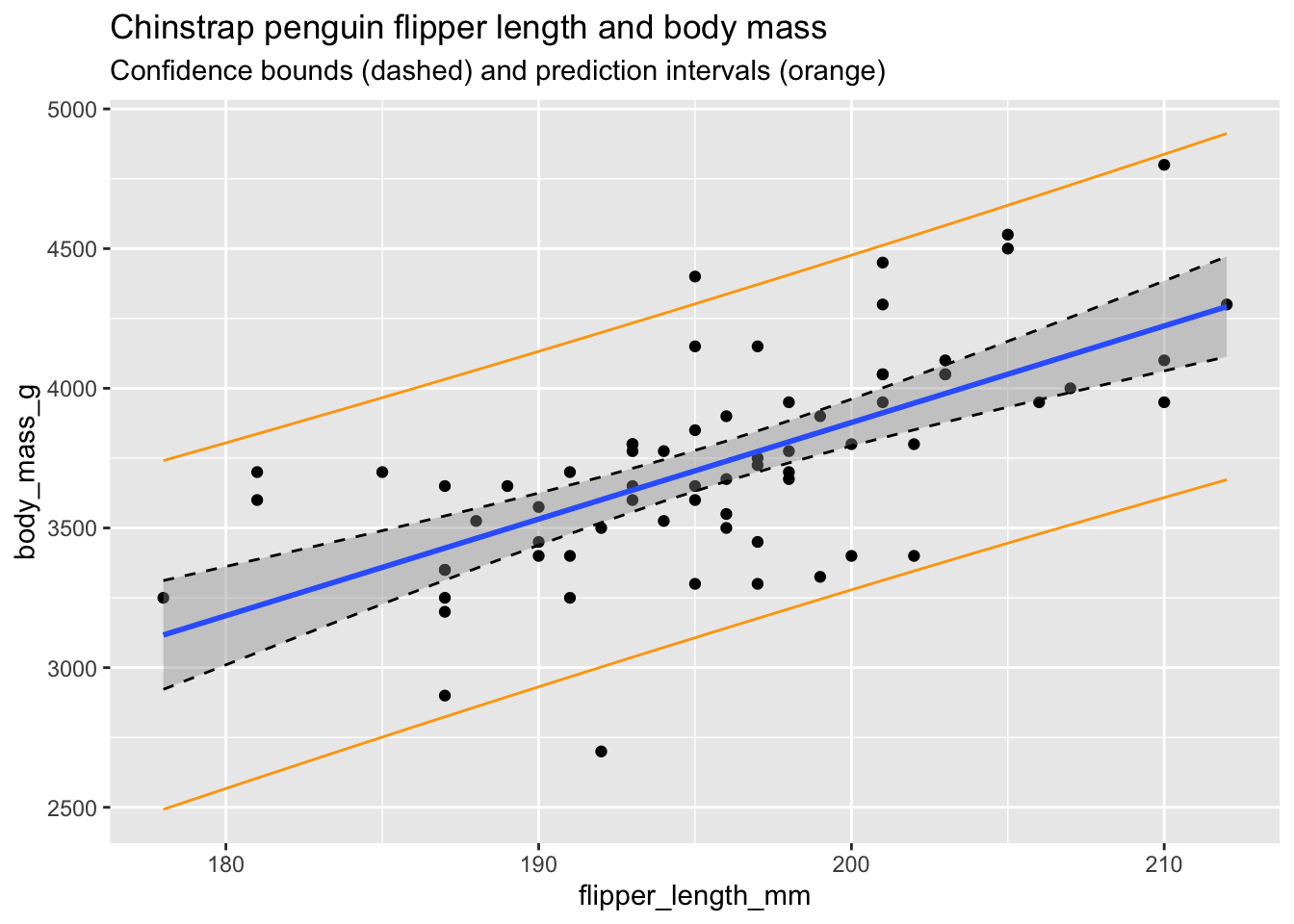

In the plot, the confidence interval about the regression line is shown in gray as usual, and is also outlined with dashed lines. The prediction interval is shown in orange.

Some things to notice:

Roughly 95% of the data falls within the orange prediction interval. While prediction intervals are predictions of future samples, it is often the case that the original data also falls in the prediction interval roughly 95% of the time.
We are 95% confident that the true population regression line falls in the gray confidence band.
The confidence band is narrowest near \((\overline{x}, \overline{y})\) and gets wider away from that central point. This is typical behavior.
We have confirmed the method that geom_smooth uses to create the confidence band.

10.3 Correlation

The correlation \(\rho\) is a number between -1 and 1 that measures the strength of the linear relationship between two random variables \(X\) and \(Y\). It is positive when \(X\) and \(Y\) tend to be large together and small together, and it is negative when large \(X\) values accompany small \(Y\) values and vice versa. A correlation of 0 indicates no linear relationship, and a correlation of \(\pm 1\) is achieved only when \(X\) and \(Y\) have an exact linear relationship.

If \(X\) and \(Y\) have means and standard deviations \(\mu_X\), \(\sigma_X\) and \(\mu_Y\), \(\sigma_Y\) respectively, then \[ \rho_{X,Y} = \frac{E\left[(X-\mu_X)(Y-\mu_Y)\right]}{\sigma_X\sigma_Y} \]

Given a sample \((x_1, y_1),\ldots, (x_n, y_n)\), we define the sample correlation coefficient \(r\) as follows:

Definition 10.2 The sample correlation coefficient is \[ r = \frac{1}{n-1} \sum ^n _{i=1} \left( \frac{x_i - \bar{x}}{s_x} \right) \left( \frac{y_i - \bar{y}}{s_y} \right) \]

The \(i^{\text{th}}\) term in the sum for \(r\) will be positive whenever:

Both \(x_i\) and \(y_i\) are larger than their means \(\bar{x}\) and \(\bar{y}\).
Both \(x_i\) and \(y_i\) are smaller than their means \(\bar{x}\) and \(\bar{y}\).

It will be negative whenever

\(x_i\) is larger than \(\bar{x}\) while \(y_i\) is smaller than \(\bar{y}\).
\(x_i\) is smaller than \(\bar{x}\) while \(y_i\) is larger than \(\bar{y}\).

Since \(r\) is a sum of these terms, \(r\) will tend to be positive when \(x_i\) and \(y_i\) are large and small together, and \(r\) will tend to be negative when large values of \(x_i\) accompany small values of \(y_i\) and vice versa.

Note that correlation is symmetric in \(x\) and \(y\), and is not dependent on the assignment of explanatory and response to the variables.

Example The correlation between carb and optden in the Formaldehyde data set is \(r = 0.9995232\), which is quite close to 1. The plot showed these data points were almost perfectly on a line.

cor(Formaldehyde$carb, Formaldehyde$optden)

## [1] 0.9995232

Example Here are scatterplots of all three penguin species:

penguins %>% ggplot(aes(x = flipper_length_mm, y = body_mass_g, color=species)) +
  geom_point(size = 0.1) +
  facet_grid(.~species)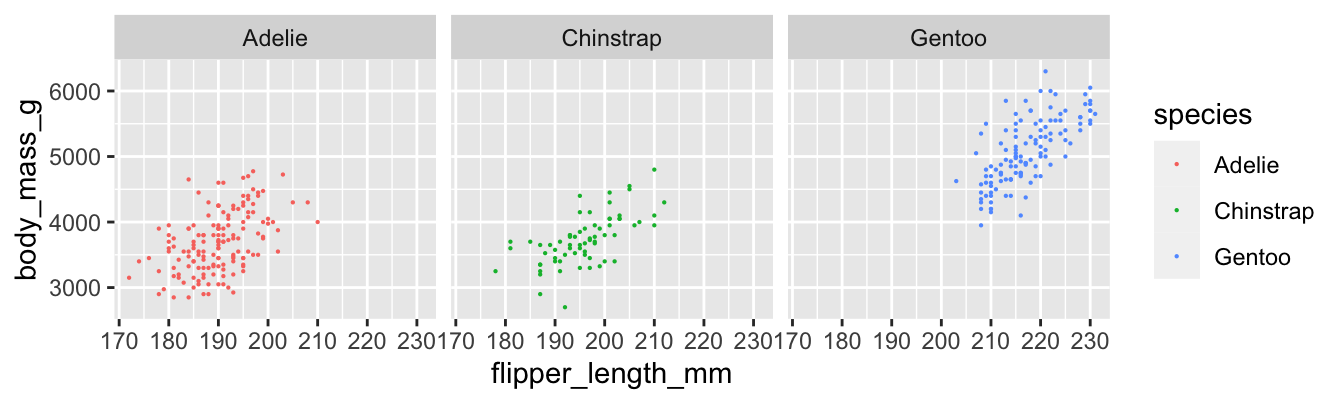

The correlations between flipper length and body mass for each species are:

penguins %>% group_by(species) %>%
  summarize(correlation = cor(flipper_length_mm, body_mass_g, use="complete.obs"))

## # A tibble: 3 x 2
##   species   correlation
##   <fct>           <dbl>
## 1 Adelie          0.468
## 2 Chinstrap       0.642
## 3 Gentoo          0.703

We see that the Gentoo penguins have the strongest linear relationship between flipper length and body mass, with \(r = 0.703\). The Adelie penguins have the weakest, with \(r = 0.468\). The difference is visible in the plots, where the points for Adelie penguins have a looser clustering. All three scatterplots do exhibit a clear linear pattern.

Example In the child tasks study, the correlation between child’s age and time on the STT trail B is \(r = -0.593\).

cor(child_tasks$age_in_months, child_tasks$stt_cv_trail_b_secs)

## [1] -0.5928128

The negative correlation indicates that older children post faster times on the test. This is visible in the scatterplot as a downward trend as you read the plot from right to left.

Note that correlation is a unitless quantity. The term \((x_i - \bar{x})/\sigma_x\) has the same units (for \(x\)) in the numerator and denominator, so they cancel, and the \(y\) term is similar. This means that a linear change of units will not affect the correlation coefficient:

child_tasks$age_in_years <- child_tasks$age_in_months / 12
cor(child_tasks$age_in_years, child_tasks$stt_cv_trail_b_secs)

## [1] -0.5928128

It it clear (from experience, not from a statistical point of view) that there is a causal relationship between a child’s age and their ability to connect dots quickly. As children age, they get better at most things. However, correlation is not causation. There are many reasons why two variables might be correlated, and \(x\) causes \(y\) is only one of them.

As a simple example, the size of children’s shoes are correlated with their reading ability. However, you cannot buy a child bigger shoes and expect that to make them a better reader. The correlation between shoe size and reading ability is due to a common cause, age. In this example, age is a lurking variable, important to our understanding of both shoe size and reading ability, but not included in the correlation.

10.4 Geometry of regression

In this section, we establish two geometric facts about the least squares regression line.

We assume data is given as \((x_1,y_1), \dotsc, (x_n,y_n)\), and that the sample means and standard deviations of the data are \(\bar{x}\), \(\bar{y}\), \(s_x\), \(s_y\).

Theorem 10.1

The least squares regression line passes through the point \((\bar{x},\bar{y})\).
The least squares regression line has slope \(\hat \beta_1 = r \frac{s_y}{s_x}\).

Before turning to the proof, we illustrate with chinstrap penguins:

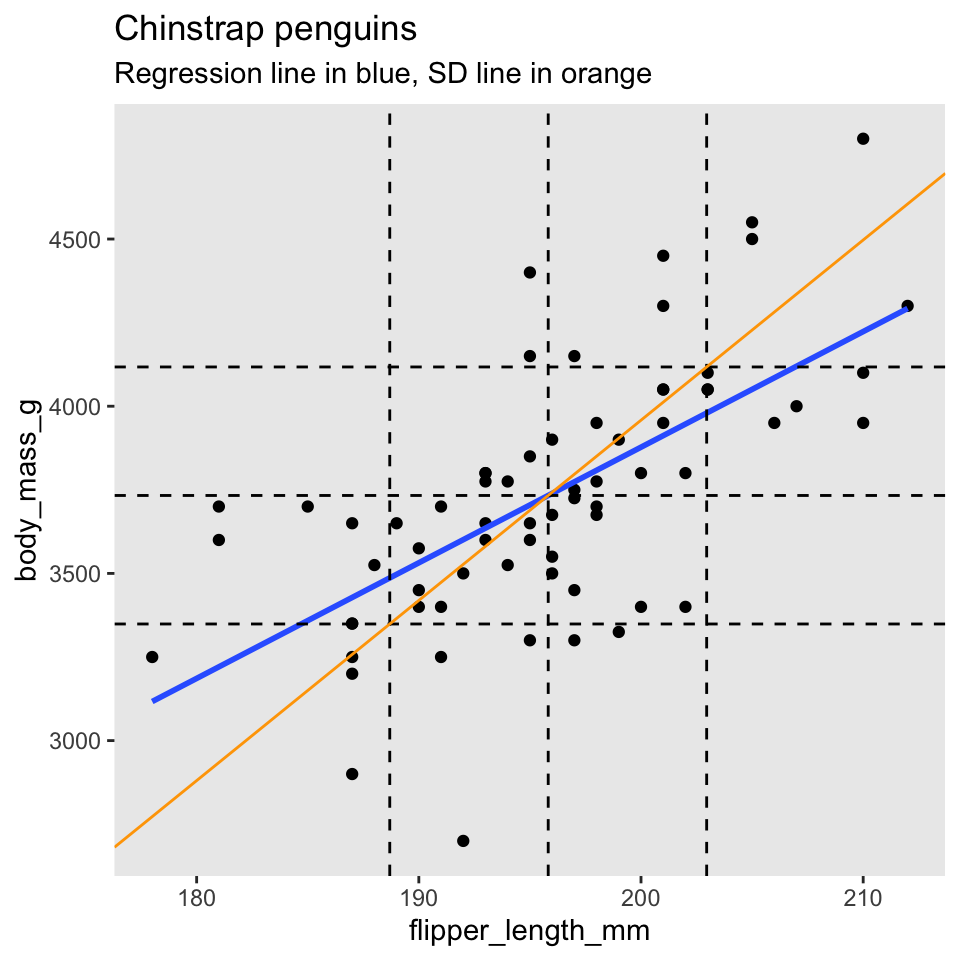
In this picture, there are vertical dashed lines at \(\bar{x}\) and \(\bar{x} \pm s_x\). Similarly, horizontal dashed lines are at \(\bar{y}\) and \(\bar{y} \pm s_y\). The regression line is thick and blue. The central dashed lines intersect at the point \((\bar{x},\bar{y})\) and this confirms part 1 of the theorem: the regression line passes through the “center of mass” of the data.

To better understand part 2 of the theorem, the scale of the plot has been adjusted so that one standard deviation is the same distance on both the \(x\) and \(y\) axes. The diagonal orange line in the picture is called the standard deviation line and it has slope \(\frac{s_y}{s_x}\). Since one SD appears the same length both horizontally and vertically in the plot, the SD line appears at a \(45^\circ\) angle, with apparent slope 1. When looking at scatterplots, the SD line is the visual axis of symmetry of the data. But the SD line is not the regression line. The regression line is always flatter than the SD line. Since the regression line has slope \(r \frac{s_y}{s_x}\), it appears in our scaled figure to have slope \(r\), in this case 0.64. In other words, the correlation coefficient \(r\) describes how much flatter the regression line will be than the diagonal axis of the data.

Proof of Theorem 10.1

The regression line is given by \(y = \hat \beta_0 + \hat \beta_1 x\). The error for each data point is \(\hat \epsilon_i = y_i - \hat{y_i} = y_i - \hat \beta_0 - \hat \beta_1 x_i\). The coefficients \(\hat \beta_0\) and \(\hat \beta_1\) are chosen to minimize the two variable function

\[ SSE(\beta_0,\beta_1) = \sum_i \left(y_i - \beta_0 - \beta_1 x_i\right)^2 \]

This minimum will occur when both partial derivatives of SSE vanish. That is, the least squares regression line satisfies \[ \frac{\partial SSE}{\partial \beta_0} = 0 \quad \text{and} \quad \frac{\partial SSE}{\partial \beta_1} = 0.\]

First compute the partial derivative with respect to \(\beta_0\) (keeping in mind that all \(x_i\) and \(y_i\) are constants):

\[ \frac{\partial SSE}{\partial \beta_0} = -2 \sum_i (y_i - \beta_0 - \beta_1 x_i) \]

Setting this equal to zero and dividing by \(n\),

\[ 0 = \frac{1}{n} \sum_i (y_i - \beta_0 - \beta_1 x_i) = \bar{y} - \beta_0 - \beta_1 \bar{x} \]

Therefore \(\bar{y} = \hat \beta_0 + \hat \beta_1 \bar{x}\) or in other words, the point \((\bar{x}, \bar{y})\) lies on the regression line.

This proves part 1 of the theorem. For part 2, observe that the slope of the regression line won’t change if we shift all data points along either the \(x\) or \(y\) axis. So from here on we assume that both \(\bar{x}\) and \(\bar{y}\) are zero. In that case, we manipulate the formulas for \(s_x\) and the correlation coefficient \(r\) as follows:

\[ s_x = \sqrt{\frac{\sum(x_i-\bar{x})^2}{n-1}} \implies \sum_i x_i^2 = (n-1)s_x^2 \] \[ r = \frac{1}{n-1}\sum\left(\frac{x_i-\bar{x}}{s_x}\right)\left(\frac{y_i-\bar{y}}{s_y}\right) \implies \sum_i x_i y_i = (n-1)s_x s_y r \]

Now compute the partial derivative of SSE with respect to \(\beta_1\):

\[ \frac{\partial SSE}{\partial \beta_1} = -2 \sum_i (y_i - \beta_0 - \beta_1 x_i)x_i \]

Setting this to zero we find:

\[ 0 = \sum_i x_i y_i - \beta_0 \sum_i x_i - \beta_1 \sum_i x_i^2 \]

Since \(\bar{x} = 0\) the middle sum vanishes, and we have \[ 0 = (n-1)s_x s_y r - \beta_1 (n-1)s_x^2 \]

Finally, solve for \(\beta_1\) to get \(\hat \beta_1 = r\frac{s_y}{s_x}\), which is part 2 of the theorem.

10.5 Inference

How can we detect a relationship between two numeric variables? Given a sample \((x_1,y_1), \dotsc, (x_n,y_n)\), the correlation coefficient \(r\) and the regression line \(y = \hat \beta_0 + \hat \beta_1 x\) both describe a linear relationship between \(x\) and \(y\). However, the correlation and the regression line both depend on the sample. A different sample would lead to different statistics. How do we decide if the one sample we have available gives evidence of a linear relationship between the two variables? The answer is to use hypothesis testing.

The natural null hypothesis is that there is no linear relationship between \(x\) and \(y\). To make this precise mathematically, observe that under this null hypothesis, the slope of the regression line would be zero. That is, the line would be flat. The hypothesis test then becomes:

\[ H_0 : \beta_1 = 0, \quad H_a : \beta_1 \neq 0 \]

Since the slope of the regression line is directly proportional to the correlation coefficient, an equivalent test is:

\[ H_0 : \rho = 0, \quad H_a : \rho \neq 0 \]

Rejecting \(H_0\) means that there is a linear relationship between \(x\) and \(y\), or equivalently that \(x\) and \(y\) are correlated.

To run this test, assume \(H_0\), then observe a sample. From the sample, compute the test statistic, which is the slope of the regression line. Then estimate the probability of observing such a slope (or an even less likely slope) under the assumption that the true slope is actually 0. This probability is the \(p\)-value for the test.

In R, these computations are done by the summary command applied to the linear model constructed by lm.

Example Is there a correlation between chinstrap penguin flipper length and body mass? If \(\beta_1\) is the true slope of the regression line, we test the hypotheses \[ H_0 : \beta_1 = 0, \quad H_a : \beta_1 \neq 0 \]

The summary command produces quite a bit of output.

summary(chinstrap_model)

## 
## Call:
## lm(formula = body_mass_g ~ flipper_length_mm, data = chinstrap)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -900.90 -137.45  -28.55  142.59  695.38 
## 
## Coefficients:
##                    Estimate Std. Error t value Pr(>|t|)    
## (Intercept)       -3037.196    997.054  -3.046  0.00333 ** 
## flipper_length_mm    34.573      5.088   6.795 3.75e-09 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 297 on 66 degrees of freedom
## Multiple R-squared:  0.4116, Adjusted R-squared:  0.4027 
## F-statistic: 46.17 on 1 and 66 DF,  p-value: 3.748e-09

The \(p\)-value we need for this hypothesis test is given in the Coefficients section, at the end of the flipper_length_mm line. It is labeled Pr(>|t|). For this hypothesis test, \(p = 3.75\times 10{-9}\) and it is significant. The *** following the value means that the results are significant at the \(\alpha = 0.001\) level.

We reject \(H_0\) and conclude that there is a significant linear relationship between flipper length and body mass for chinstrap penguins.

Example Lifting weights can build muscle strength. Scientific studies require detailed information about the body during weight lifting, and one important measure is the time under tension (TUT) during muscle contraction. However, time under tension is difficult to measure. The best measurement comes from careful human observation of a video recording, which is impractical for a large study. In their 2020 paper³³, Viecelli et. al. used a smartphone’s accelerometer to estimate the time under tension for various common machine workouts. They also used a video recording of the workout to do the same thing. Could the much simpler and cheaper smartphone method replace the video recording?

The data is available as accelerometer in the fosdata package.

accelerometer <- fosdata::accelerometer

In this example, we focus on the abductor machine during the Rep mode of the contraction. The data set contains observations tagged as outliers, which we remove.

abductor <- accelerometer %>%
  filter(machine == "ABDUCTOR") %>%
  filter(stringr::str_detect(contraction_mode, "Rep")) %>% 
  filter(!rater_difference_outlier & 
           !smartphone_difference_outlier & 
           !video_smartphone_difference_outlier)

Let’s start by looking at a plot. Following the authors of the paper, we will create a Bland-Altman plot. A Bland-Altman plot is used when there are two measurements of the same quantity, especially when one is considered the “gold standard.” We plot the difference of the two measurements versus the mean of the two measurements.

abtimediff <- abductor %>%
  mutate(difference = smartphones_mean_ms - video_rater_mean_ms,
         mean_time = (video_rater_mean_ms + smartphones_mean_ms)/2)
abtimediff %>%
  ggplot(aes(x = mean_time/1000, y = difference/1000)) +
  geom_point() +
  labs(x = "Mean time estimate (sec)",
       y = "Difference in Estimates (sec)",
       title = "Bland-Altman plot of video and smartphone measurements")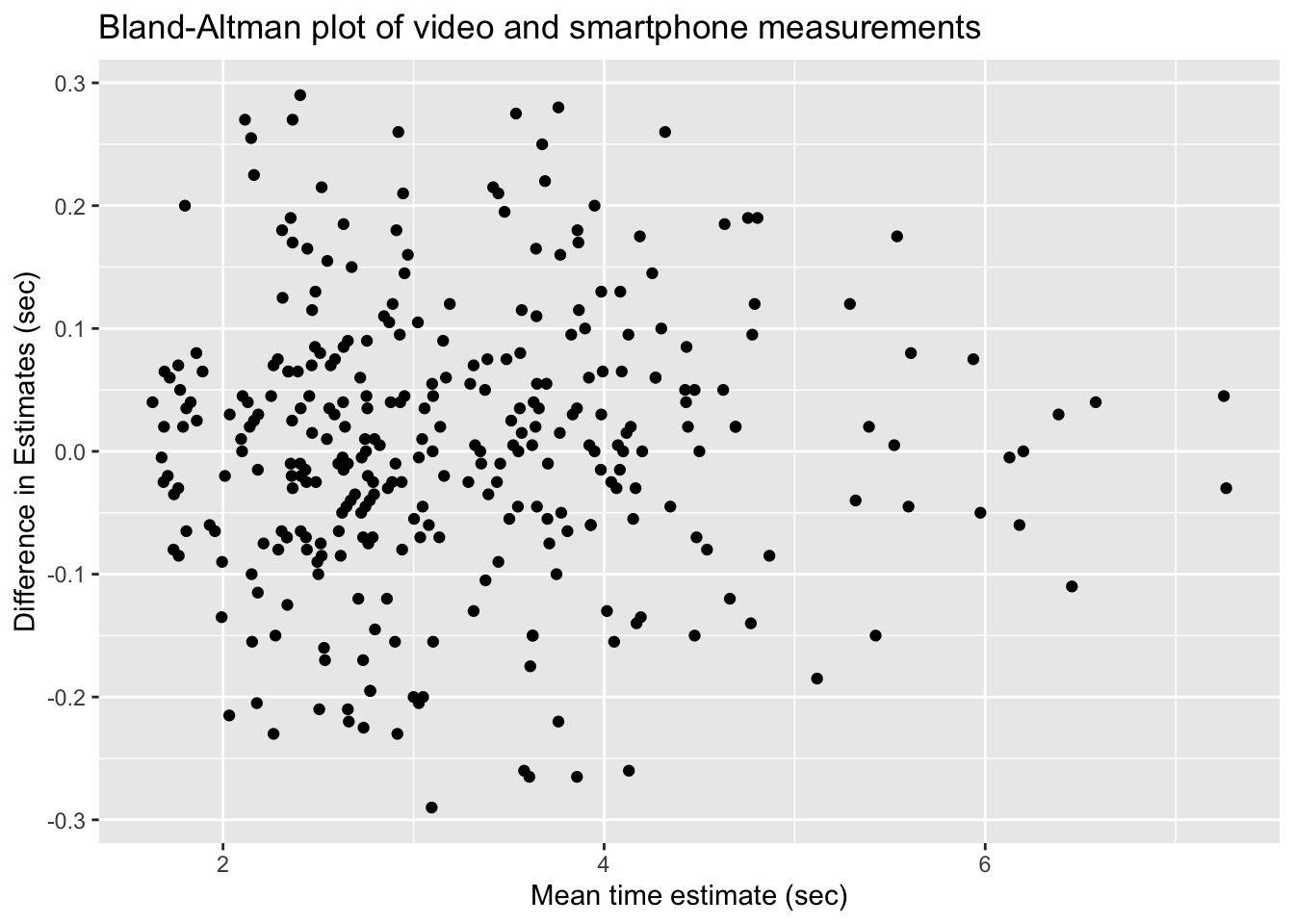

If the phone measurement is a good substitute for the video measurement, the difference of the measurements should have small standard deviation, have mean zero, and not depend on the mean of the measurements. We can use linear regression to assess the last two objectives.

The regression line through these points should have a slope and an intercept of 0. Indeed, if the intercept is not zero (but the slope is zero), then that would indicate a bias in the smartphone measurements. If the slope is not zero, then that would indicate that the smartphone estimate is not working consistently through all of the time intervals. So, let’s perform a linear regression and see what we get.

accel_mod <- lm(difference ~ mean_time, data = abtimediff)
summary(accel_mod)$coefficients

##                 Estimate  Std. Error    t value  Pr(>|t|)
## (Intercept) -6.226185392 20.37164776 -0.3056299 0.7600870
## mean_time    0.003519751  0.00600059  0.5865675 0.5579117

We cannot reject the null hypothesis that the slope is zero (\(p=0.56\)), nor the null hypothesis that the intercept is zero (\(p=0.76\)). It appears that the smartphone accelerometer measurement is a good substitute for video measurement of abductor time under tension.

10.5.1 The summary command

Let’s go through the rest of the output that R produces in the summary of a linear model. The full output of the command summary(chinstrap_model) is shown in the previous section. Here, we take it apart.

## Call: ## lm(formula = body_mass_g ~ flipper_length_mm, data = chinstrap)

The Call portion of the output reproduces the original function call that produced the linear model. Since that call happened much earlier in this chapter, it is helpful to have it here for review.

## Coefficients: ## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -3037.196 997.054 -3.046 0.00333 ** ## flipper_length_mm 34.573 5.088 6.795 3.75e-09 ***

The Coefficients portion describes the coefficients of the regression model in detail. The Estimate column gives the intercept value and the slope of the regression line, which is \(\widehat{\text{mass}} = -3037.196 + 34.573 \cdot \text{flipper length}\) as we have seen before.

The standard error column Std. Error is a measure of how accurately we can estimate the coefficient. We will not describe how this is computed. The value is always positive, and should be compared to the size of the estimate itself by dividing the estimate by the standard error. This division produces the \(t\) value, i.e. \(t = 34.573/5.088 = 6.795\) for flipper length.

Under the assumption that the errors are iid normal(0, \(\sigma\)), the test statistic \(t\) has a students t distribution, with \(n-2\) degrees of freedom. Here, \(n = 68\) is the number of penguins in the chinstrap data. We subtract 2 because we used the data to estimate two parameters (the slope and the intercept) leaving only 66 degrees of freedom. The \(p\)-value for the test is the probability that a random \(t\) is more extreme than the observed value of \(t\), which explains the notation Pr(>|t|) in the last column.

To reproduce the \(p\)-values associated with flipper_length_mm, use

 2 * ( 1 - pt(6.795, df=66) )

## [1] 3.743945e-09

where we have doubled the value because the test is two-tailed.

The final Coefficients column contains the significance codes, which are not universally loved. Basically, the more stars, the lower the \(p\)-value in the hypothesis test of the coefficients as described above. One problem with these codes are that the (Intercept) coefficient is often highly significant, even though it has a dubious interpretation. Nonetheless, it receives three stars in the output, which bothers some people.

## Residual standard error: 297 on 66 degrees of freedom ## Multiple R-squared: 0.4116, Adjusted R-squared: 0.4027 ## F-statistic: 46.17 on 1 and 66 DF, p-value: 3.748e-09

The residual standard error is an estimate of the standard deviation of the error term in the linear model. Recall that we are working with the model \(y_i = \beta_0 + \beta_1 x_i + \epsilon_i\), where \(\epsilon_i\) are assumed to be iid normal random variables with mean 0 and unknown standard deviation \(\sigma\). The residual standard error is an estimate for \(\sigma\).

Multiple R-squared is the square of the correlation coefficient \(r\) for the two variables in the model.

The rest of the output is not interesting for simple linear regression, i.e. only one explanatory variable, but becomes interesting when we treat multiple explanatory variables in Chapter 12. For now, notice that the \(p\)-value on the last line is exactly the same as the \(p\)-value for the flipper_length_mm coefficient, which was the \(p\)-value needed to test for a relationship between flipper length and body weight.

10.5.2 Inference on the slope

The most likely type of inference on the slope we will make is \(H_0: \beta_1 = 0\) versus \(H_a: \beta_1 \not = 0\). The \(p\)-value for this test is given in the summary of the linear model. However, there are times when we want a confidence interval for the slope, or to test the slope against a value other than 0. We illustrate with the following example.

Example Consider the data set Davis in the package carData. The data consists of 200 observations of the variables sex, weight, height, repwt and repht. Let’s look at a plot of patients weight versus their reported weight.

Davis <- carData::Davis
ggplot(Davis, aes(x = repwt, y = weight)) + geom_point()

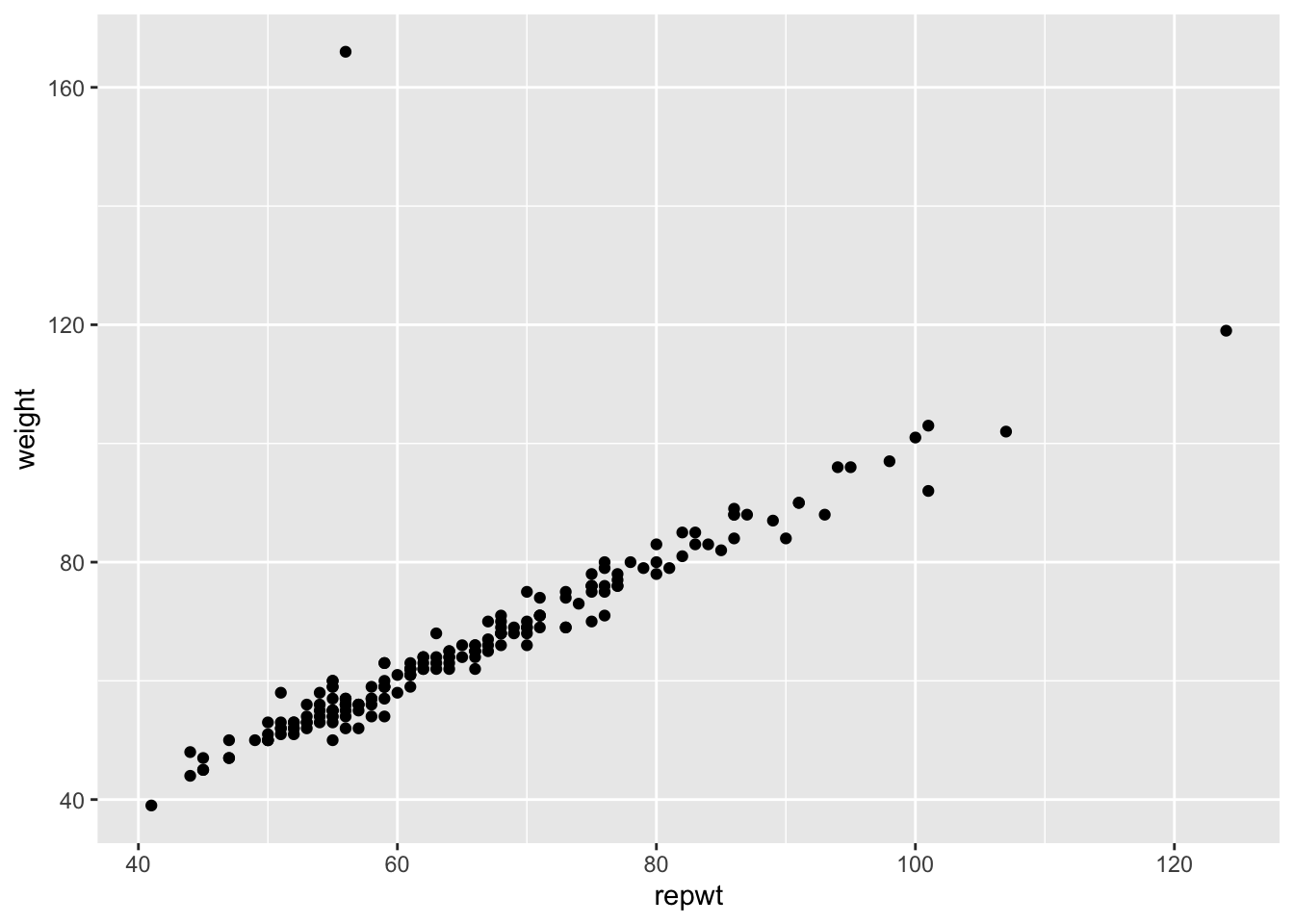
As we can see, there is a very strong linear trend in the data. There is also one outlier, who has reported weight of 56 and observed weight of 166. Let’s remove that data point:

Davis <- filter(Davis, weight != 166)

Create a linear model for weight as explained by repwt and then extract the coefficients:

modDavis <- lm(weight~repwt, data = Davis)
summary(modDavis)$coefficients

##              Estimate Std. Error   t value      Pr(>|t|)
## (Intercept) 2.7338020 0.81479433  3.355205  9.672344e-04
## repwt       0.9583743 0.01214273 78.925763 1.385270e-141

In this example, we are not interested in testing the slope of the regression line against zero, since the linear relationship is obvious.

The statement we would like to test is whether people report their weights accurately. Perhaps as people vary further from what is considered a healthy weight, they report their weights toward the healthy side. Underweight people might overstate their weight and overweight people might understate their weight. So, an interesting question here is whether the slope of the regression line is 1.

Let’s estimate the 95% confidence interval for the slope of the regression line. This interval is given by the estimate for the slope plus or minus approximately twice its standard error. From the regression coefficients data, the estimate is 0.95837 and the standard error is 0.01214, giving an interval of roughly \([.93, .98]\).

To get more precise information, can use the R function confint.

confint(modDavis,level = .95)

##                 2.5 %    97.5 %
## (Intercept) 1.1260247 4.3415792
## repwt       0.9344139 0.9823347

We are 95% confident that the true slope is in the interval \([0.934, 0.982]\)

The corresponding hypothesis test is \(H_0: \beta_1 = 1\) against \(H_a: \beta_1 \neq 1\). Since the 95% confidence interval for the slope does not contain the value 1, we can reject \(H_0\) in favor of \(H_a\) at the \(\alpha - .05\) level. We conclude that the slope is significantly different from 1, and that the population covered by this study does tend to report weights with a bias towards the mean weight.

10.6 Residual analysis

Simple linear regression fits a line to data. Inference using simple linear regression relies on the assumption that the data follows the linear model \(y_i = \beta_0 + \beta_1 x_i + \epsilon_i\). When using a linear model, it is essential to investigate whether or not the model actually makes sense. In this section, we will focus on three common problems that can occur with linear models:

The relationship between the explanatory and response variables is not linear.
There are outliers that adversely affect the model.
Our assumptions that the \(\epsilon_i\) are iid normal with identical standard deviation are violated.

There can be other problems besides these three common ones. The most straightforward way to assess problems with a model is by visual inspection of the residuals. This is more of an art than a science, and in the end it is up to the investigator to decide whether a model is accurate enough to act on the results.

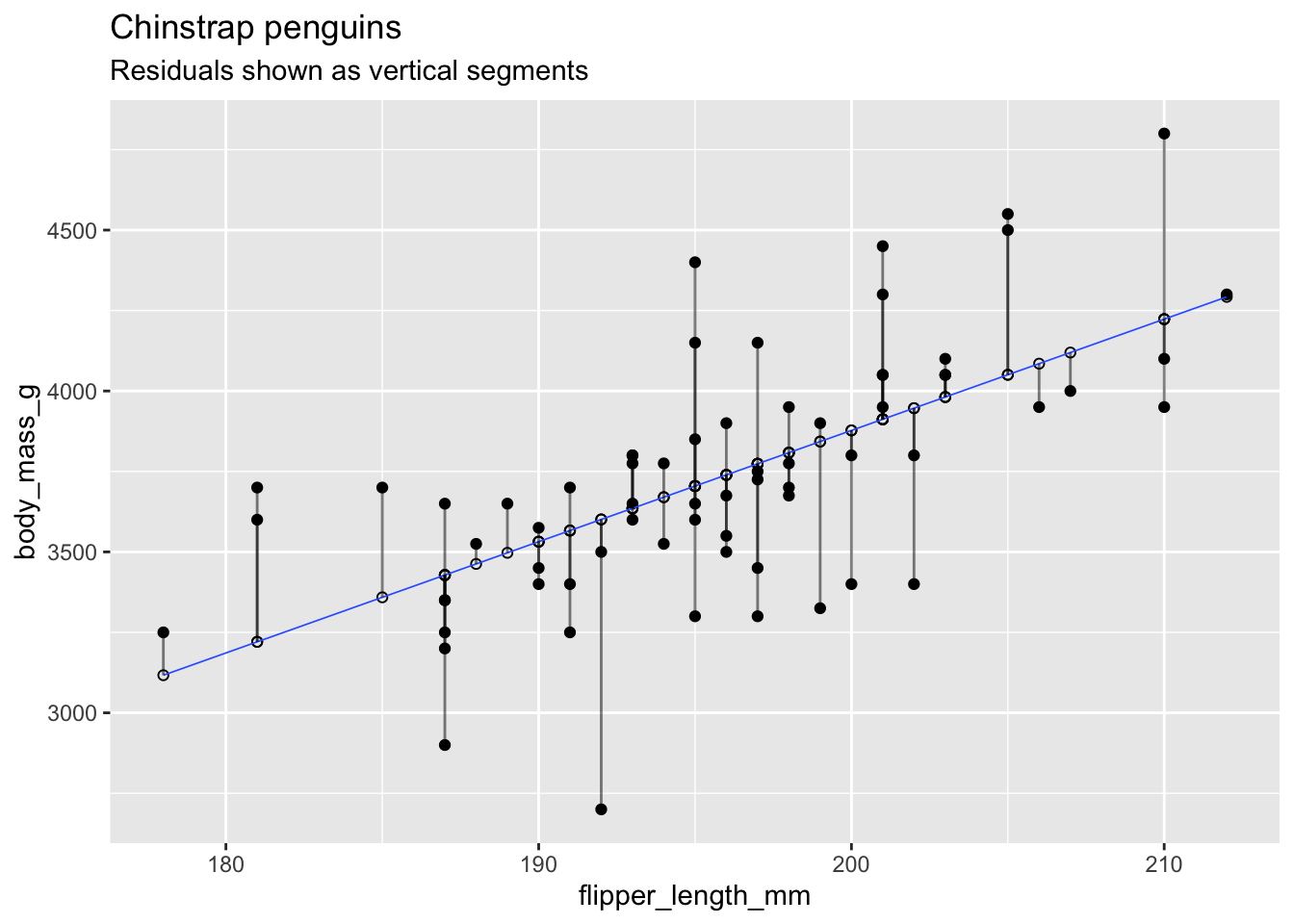
Recall that the residuals are the vertical distances between the regression line and the data points. This plot of chinstrap penguin data shows the residuals as vertical line segments. Black points are the penguin data, and the fitted points \((x_i,\hat{y_i})\) are shown as open circles. The residuals are the lengths of the segments between the actual and fitted points.

The simplest way to visualize the residuals for a linear model is to apply the base R function plot to the linear model. The plot function produces four diagnostic plots, and when used interactively it shows the four graphs one at a time, prompting the user to hit return between graphs. In RStudio the Plots panel has arrow icons that allow the user to view older plots, which is often helpful after displaying all four.

Here are the residuals for the chinstrap penguin data, visualized with plot:

plot(chinstrap_model)

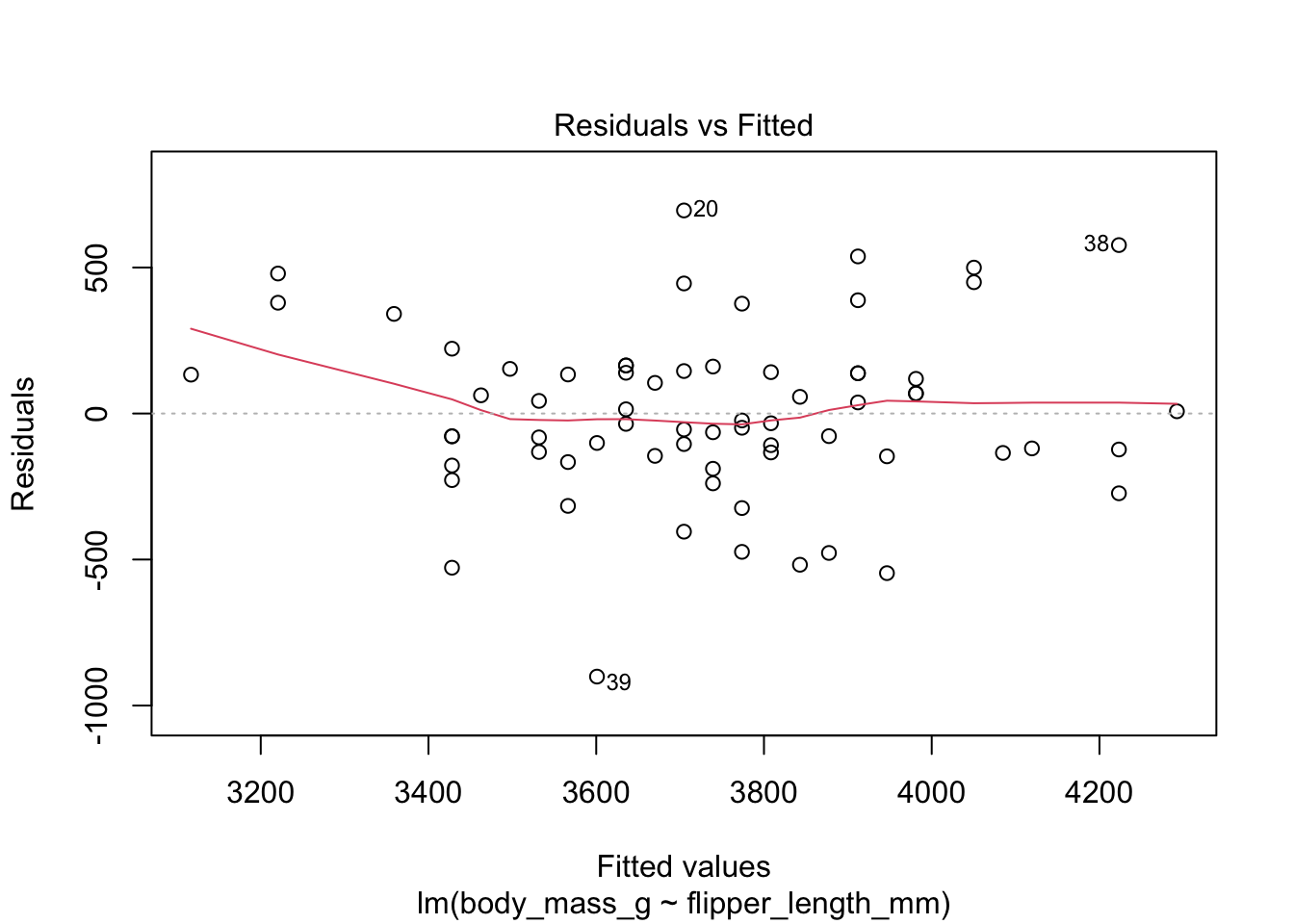
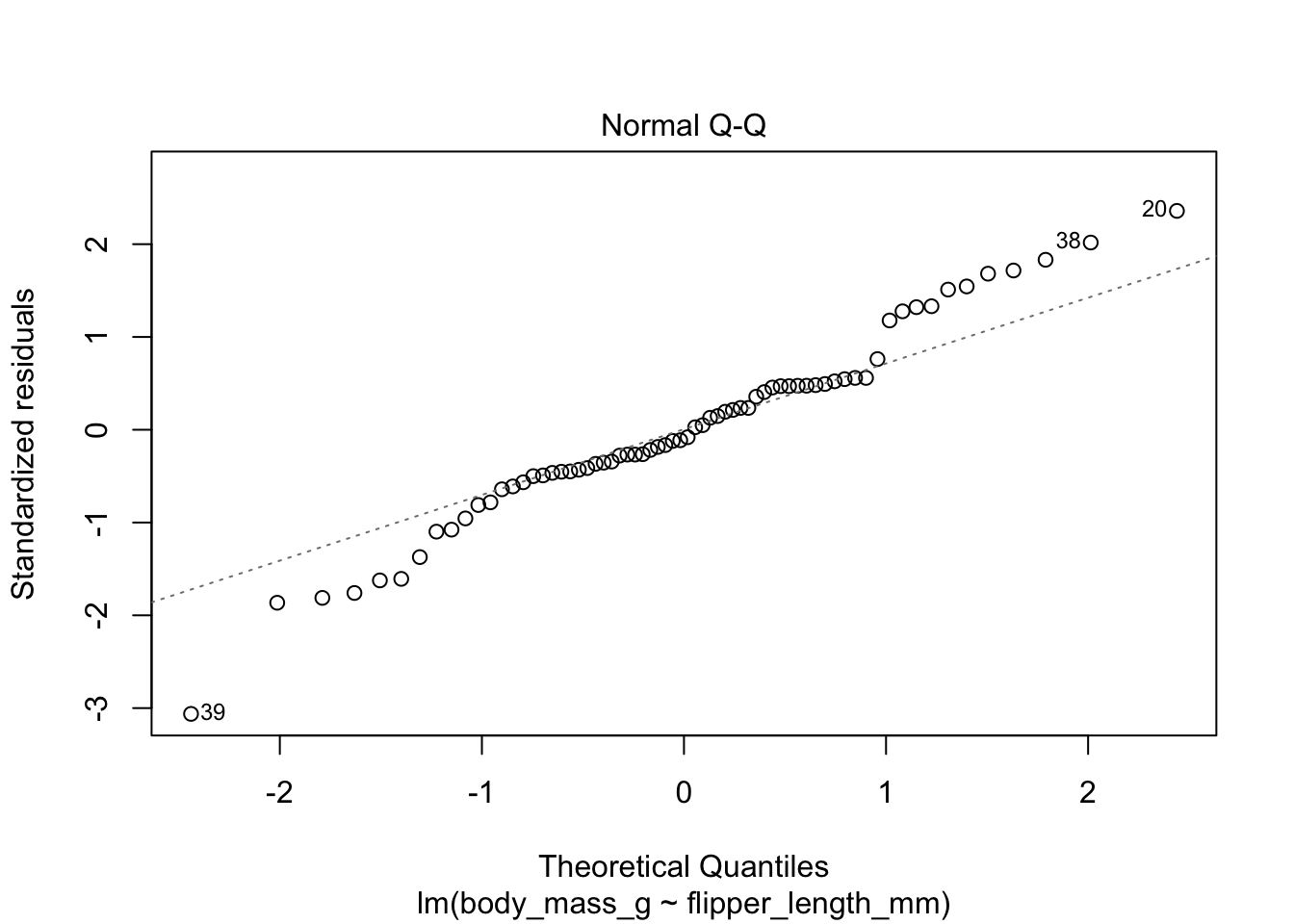
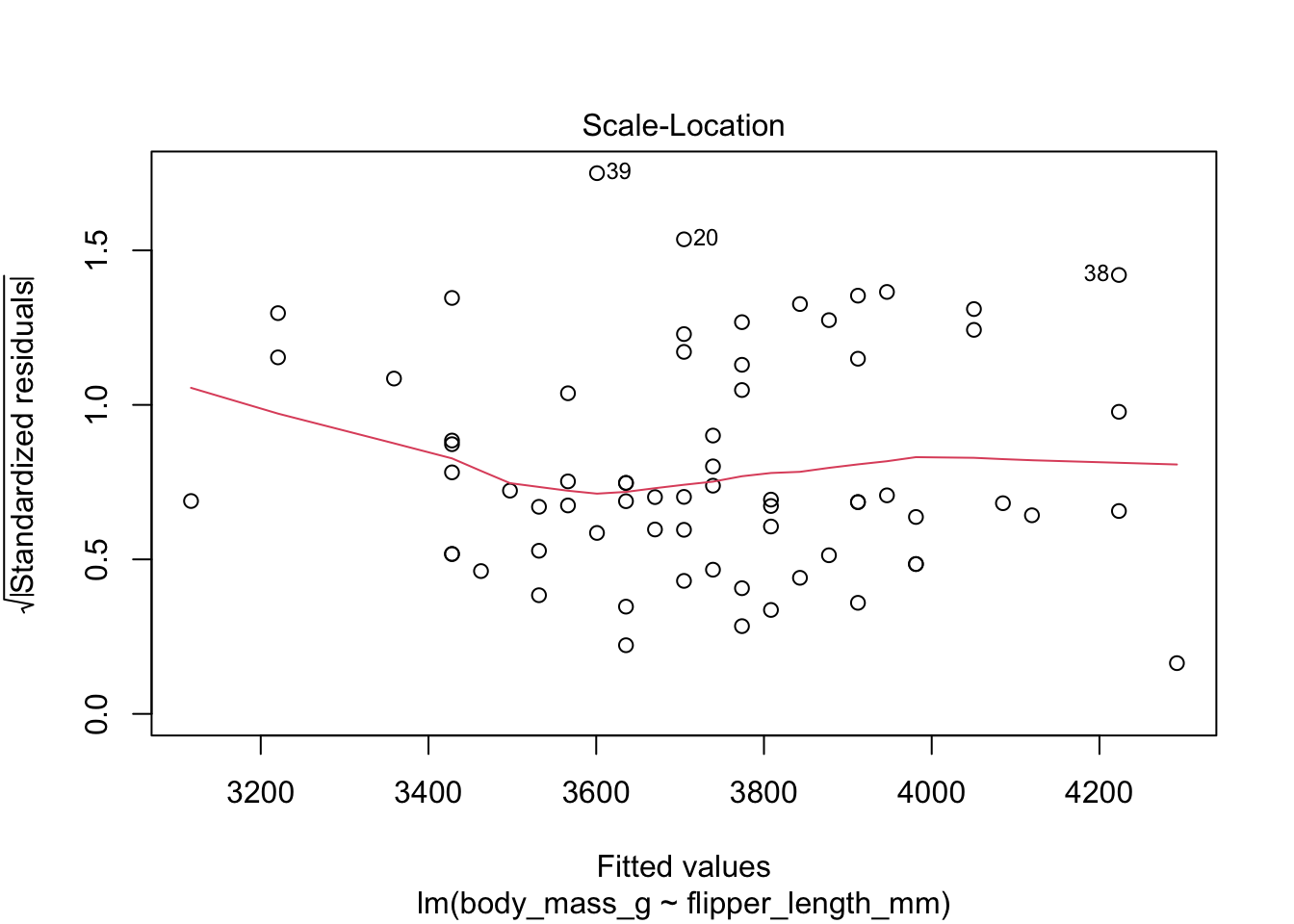
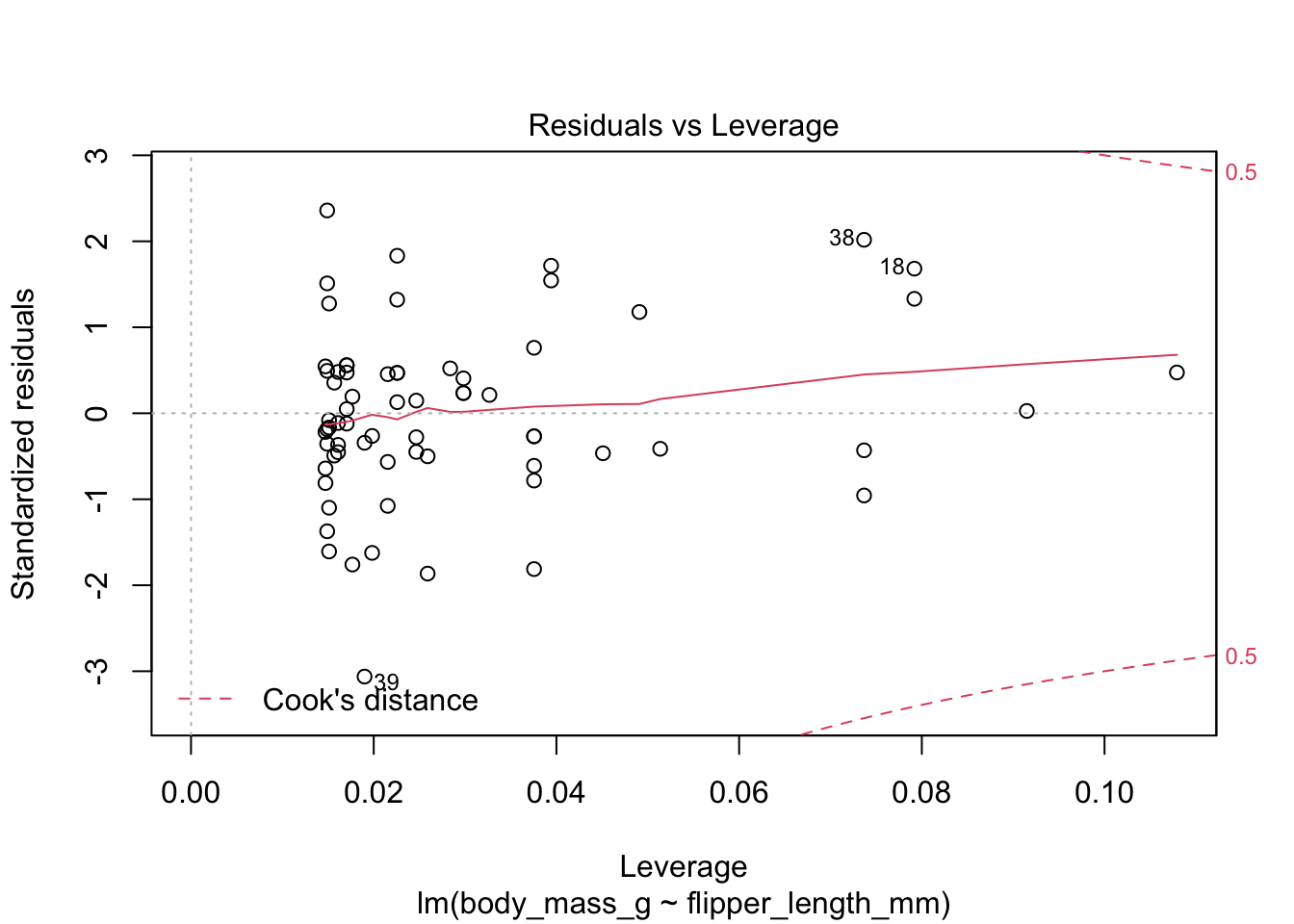
The “Residuals vs Fitted” plot shows the residuals versus the fitted values \(\hat{y_i}\). It might seem more natural to plot residuals against the explanatory variables \(x_i\), and in fact for simple linear regression it does make sense to do that. However, \(\hat{y_i}\) is a linear function of \(x_i\), so the plot produced by plot looks the same as a plot of residuals against \(x_i\), just with a different scale on the \(x\)-axis. The advantage of fitted values comes with multiple regression, where it allows for a two-dimensional plot.

The regression line is chosen to minimize the SSE of the residuals. This implies that the residuals themselves have mean zero, since a nonzero mean would allow a better fit by raising or lowering the fit line vertically. The “Residuals vs Fitted” plot shows the mean of zero as a horizontal dashed line. In the “Residuals vs Fitted” plot, ideal residuals are spread uniformly across this line.

A pattern such as a U-shape is evidence of a lurking variable that we have not taken into account. A lurking variable could be information related to the data that we did not collect, or it could be that our model should include a quadratic term. The red curve is fitted to the residuals to make patterns in the residuals more visible.

The second plot is a normal-qq plot of the residuals. Ideally, the points would fall more or less along the diagonal dotted line shown in the plot.

The “Scale Location” plot shows standardized residuals versus the fitted values. By standardizing the residuals, making them positive, and taking the square root, the visual height of the dots corresponds to the variance of the residuals. A crucial assumption for inference is that variance is constant across the fitted values, so ideally the vertical spread of dots is constant across the plot. The red fitted curve helps to visualize the variance, and we are looking to see that the red line is more or less flat.

The last plot is an analysis of outliers and leverage. Outliers are points that fit the model worse than the rest of the data. Outliers with \(x\) coordinates in the middle of the data tend to have less of an impact on the final model than outliers toward the edge of the \(x\)-coordinates. Data that falls outside the red dashed lines are high-leverage outliers, meaning that they (may) have a large effect on the final model.

The linear model for the chinstrap penguin data is a good fit, satisfies the assumptions of regression, and does not have serious outliers.

10.6.1 Linearity

In order to apply a linear model to data, the relationship between the explanatory and response variable should be linear. If the relationship is not linear, sometimes transforming the data can create new variables that do have a linear relationship. Alternatively, a more complicated non-linear model or multiple regression may be required.

Example As part of a study to map developmental skull geometry, Li et. al (2016) recorded the age and skull circumference of 56 young children. The correlation between age and skull circumference is 0.8, suggesting a strong relationship, but is it linear? Here is a plot:

skull_geometry <- fosdata::skull_geometry
ggplot(skull_geometry,aes(x=age_mos, y=circumference_cm)) +
  geom_point() + geom_smooth(method="lm") +
  labs(title="Age vs. skull circumference in young children",
       subtitle="The linear model is a poor fit")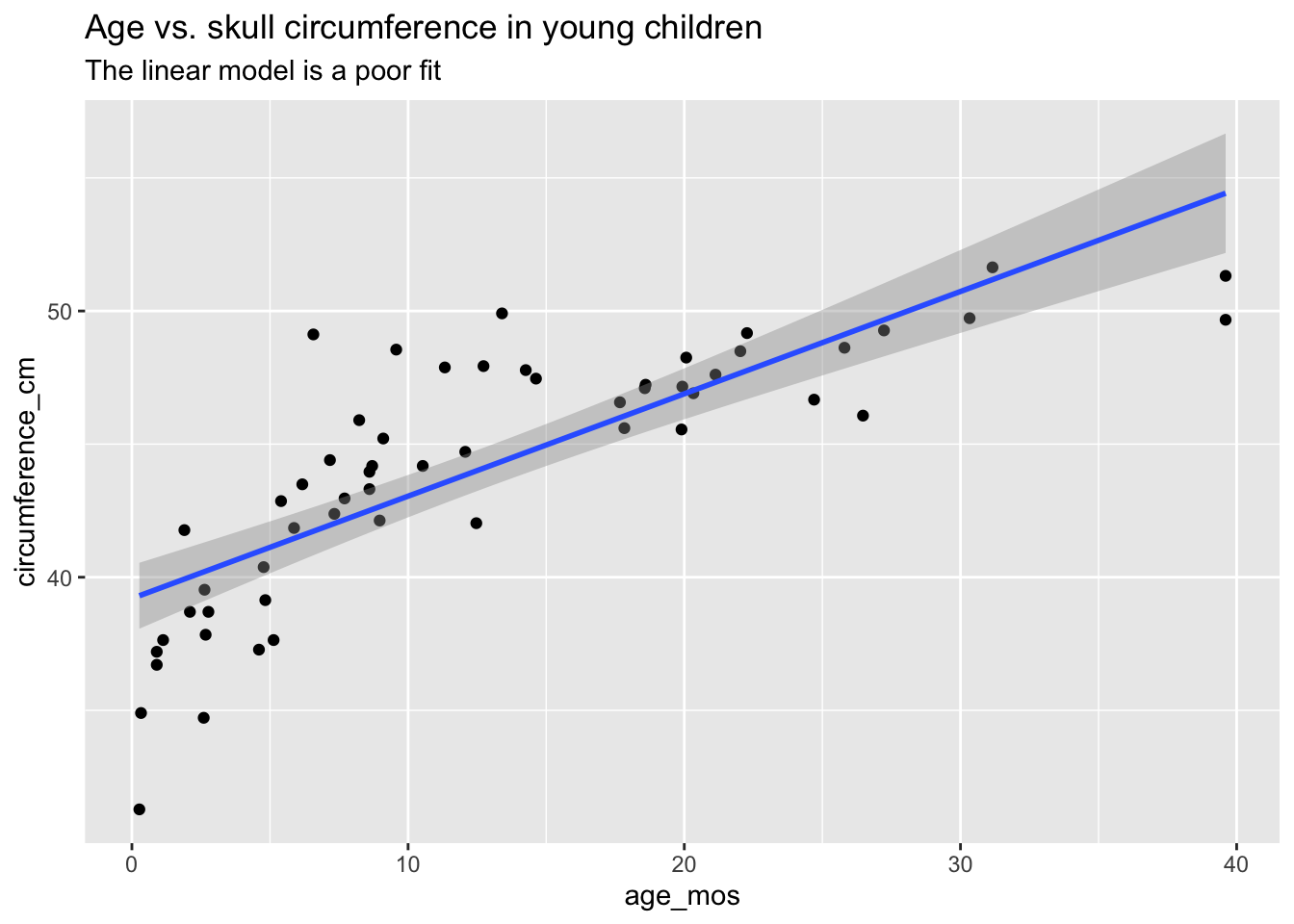

Observe that most of the younger and older children have skulls smaller than the line predicts, while children from 5-20 months have larger skulls. This U-shaped pattern suggests that the line is not a good fit for this data. The residual plot makes the U-shape even more visible:

skull_model <- lm(circumference_cm ~ age_mos, data=skull_geometry)
plot(skull_model, which=1)   # which=1 selects the first of the four plots for display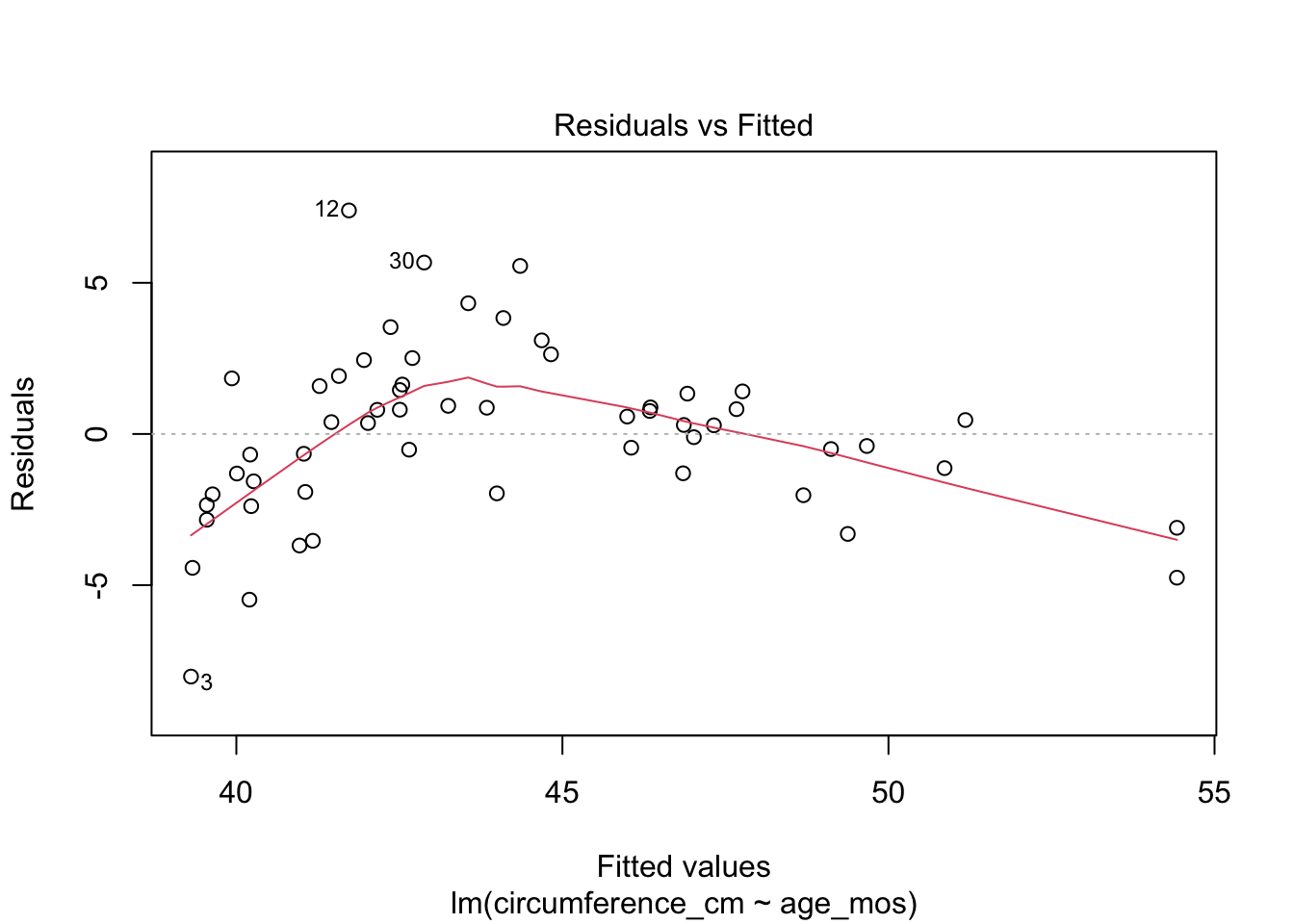

A good growth chart for skull circumference would fit a curve to this data. Curve fitting is beyond the scope of this book, but is treated in these fine references: ??.

10.6.2 Heteroscedasticity

A key assumption for inference with linear models is that the residuals have constant variance. This is called homoscedasticity. Its failure is called heteroscedasticity, and this is one of the most common problems with linear regression.

Heteroscedastic residuals display changing variance across the fitted values, typically with variance increasing from left to right as the size of the data increases:

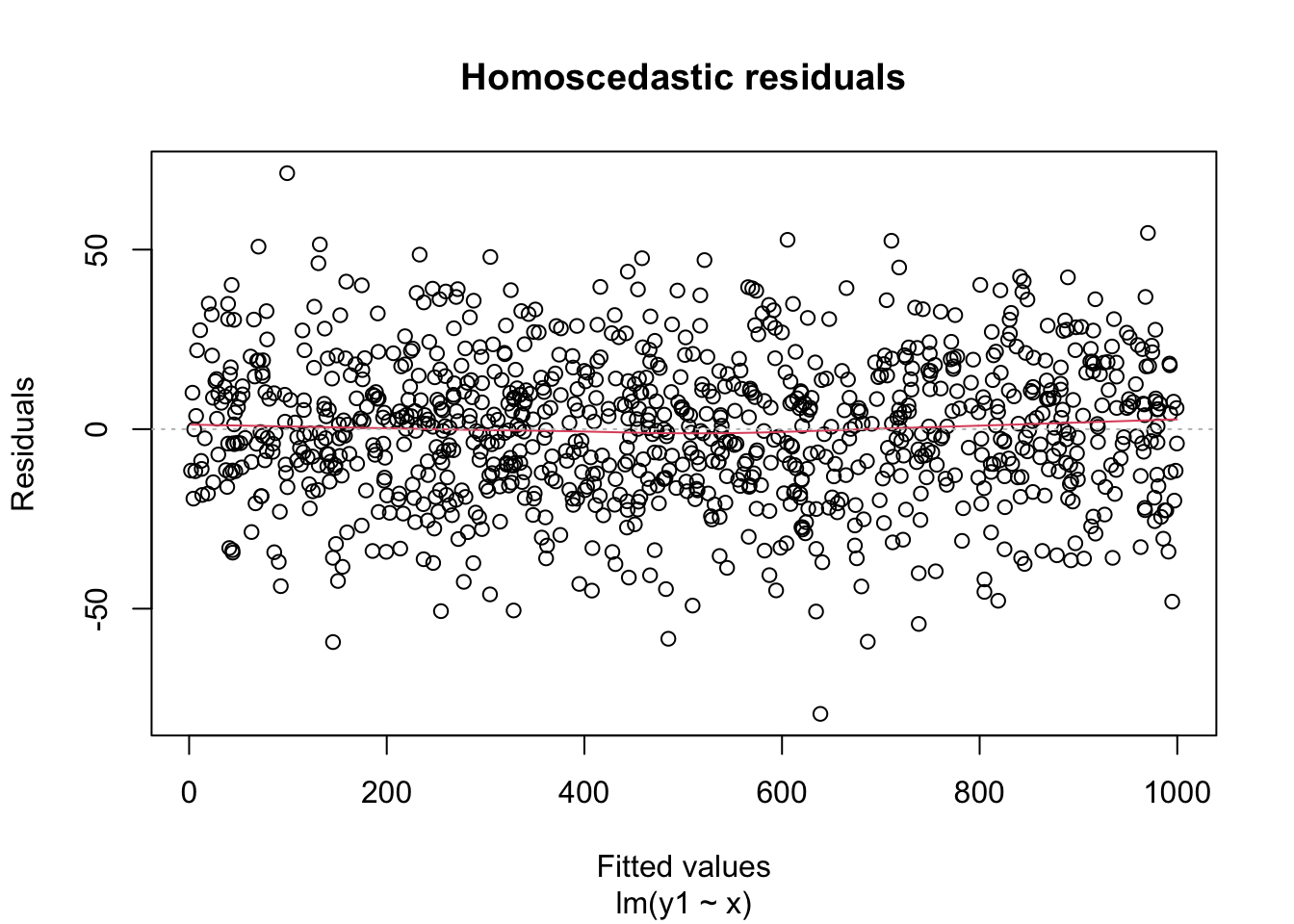
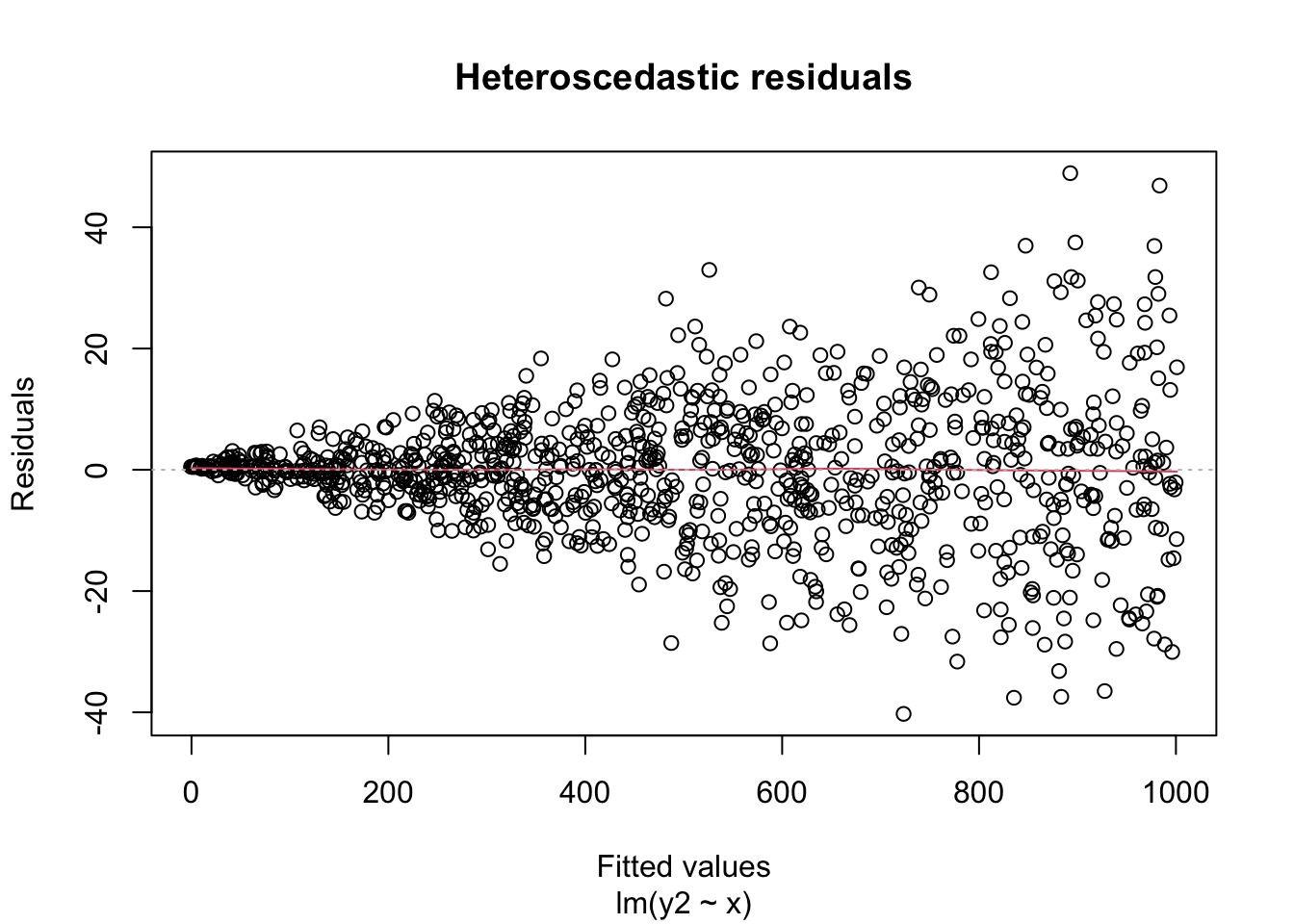
Heteroscedasticity frequently occurs because the true errors are a percentage of the data values, rather than an additive error. For example, many expenditures related to household income are heteroscedastic, since households spend a percentage of their income rather than a fixed amount.

Example Consider the leg_strength data set in the fosdata package. Loss of leg strength is a predictor of falls in elderly adults, but measuring leg strength requires expensive laboratory equipment. Researchers³⁴ built a simple setup using a Nintendo WiiFit balance board and compared measurements using the Wii to measurements using the laboratory stationary isometric muscle apparatus (SID).

leg_strength <- fosdata::leg_strength
leg_strength %>% 
  ggplot(aes(x = mean_wii, y = mean_sid)) + 
  geom_point() + 
  geom_smooth(method="lm", se = FALSE) +
  labs(x = "SID", y = "WII", title = "Mean leg strength as measured by WII balance board vs SID")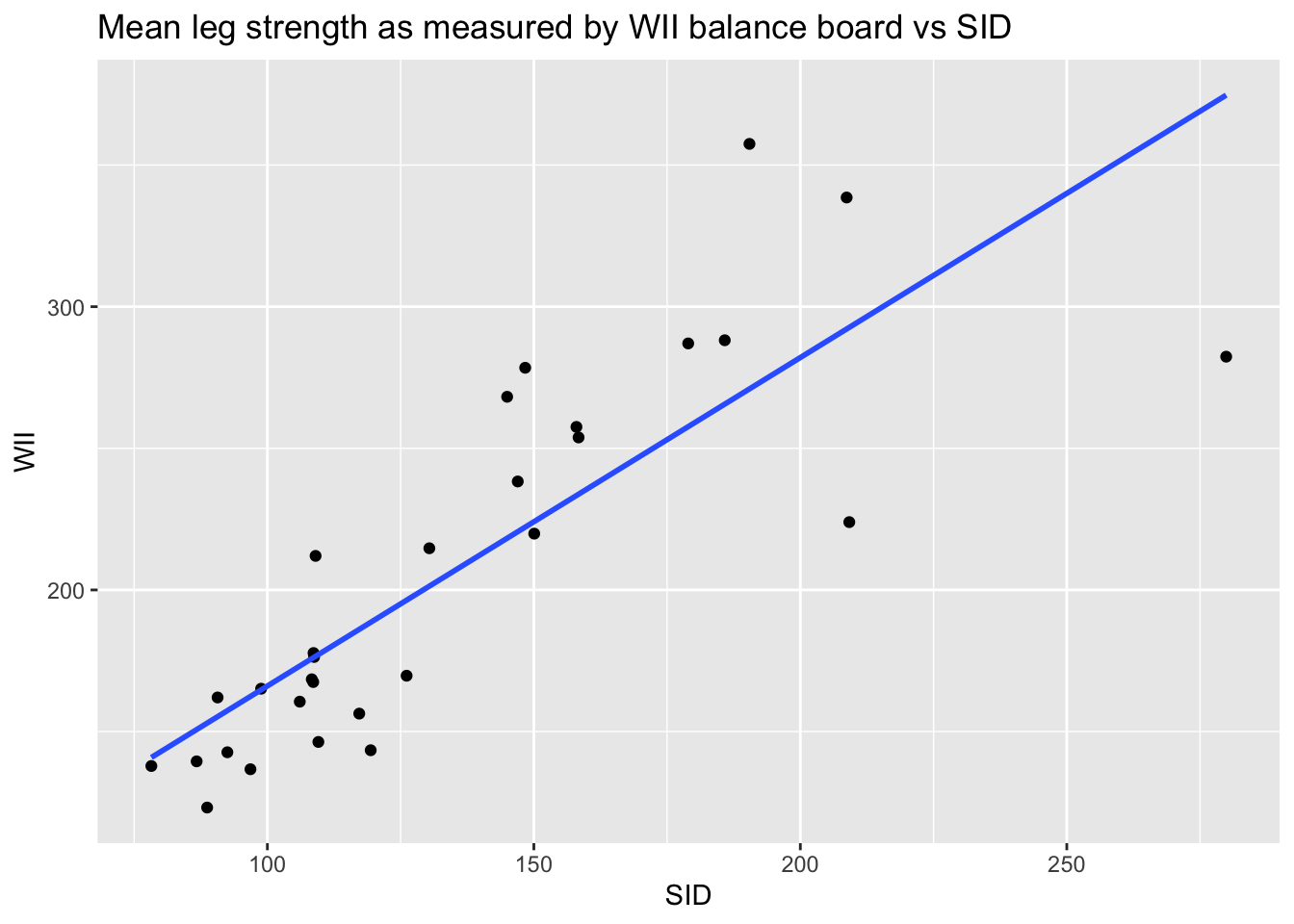

The goal of the experiment is to replace the accurate SID measurement with the inexpensive WII measurement. The graph makes it clear that the WII works less well for stronger legs. The “Residuals vs. Fitted” plot shows this heteroscedasticity as well, but the best view comes from the third of the diagnostic plots:

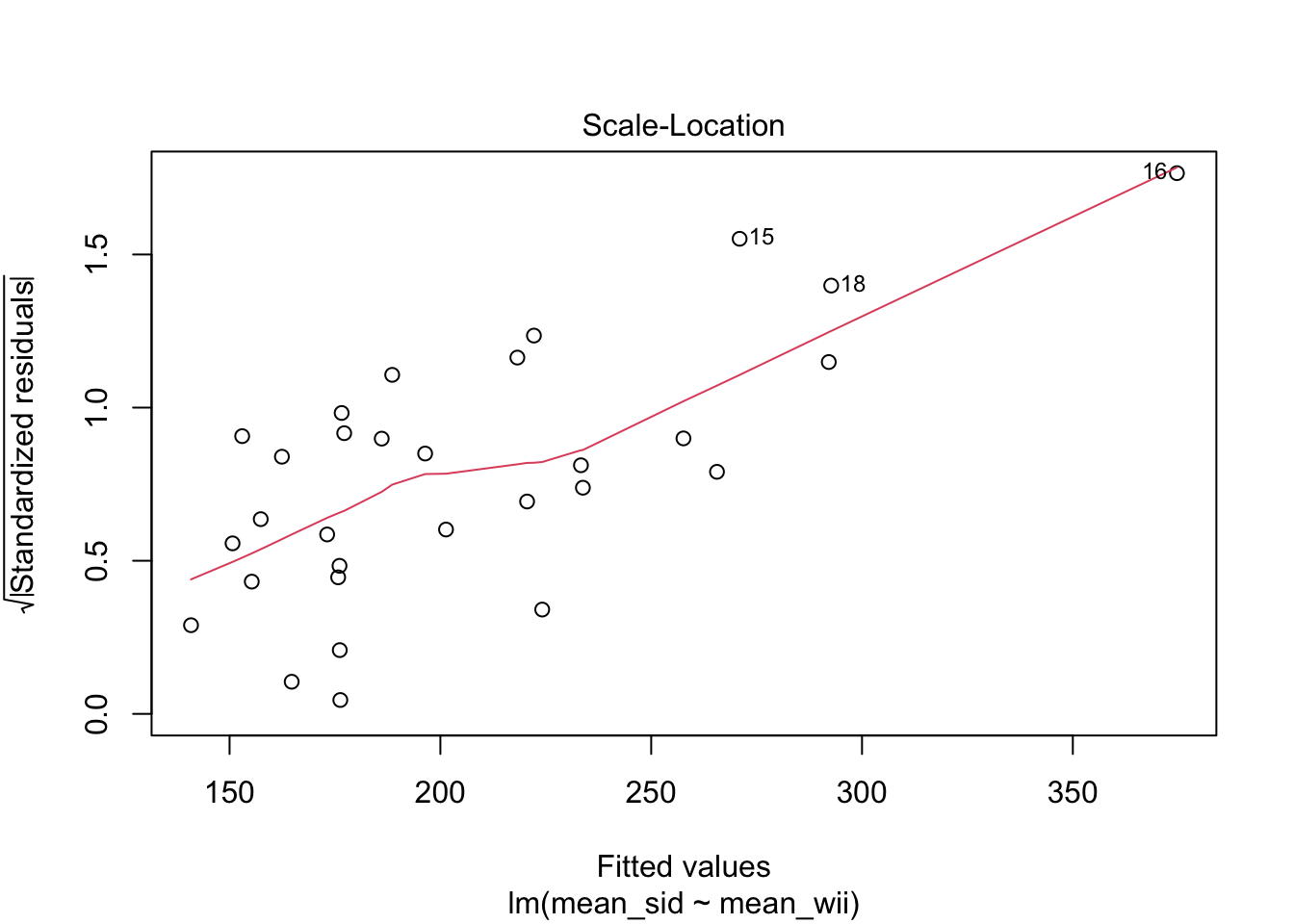
wii_model <- lm(mean_sid ~ mean_wii, data=leg_strength)
plot(wii_model, which=3)

There is a clear upward slant to the points, emphasized by the red line. This data is heteroscedastic. Using the linear model for inference would be questionable. You could still use the regression line to convert WII balance readings to SID values, but you would need to be aware that higher WII readings would have higher variance.

Example Right skew variables are common. When variables are right skew, it means they contain a large number of small values and a small number of large values. For such variables, we are more interested in the order of magnitude of the values: is the value in the 10’s, 1000’s, millions? These variables will almost certainly be heteroscedastic.

In this example, we look at Instagram posts by gold medal winning athletes in the 2016 Rio Olympic Games, which is in the rio_instagram data frame in the fosdata package. For each athlete, we plot the number of Instagram followers and the maximum number of “likes” for any of their posts during the Olympics.

rio_instagram <- fosdata::rio_instagram
rio_instagram %>% 
  filter(!is.na(n_follower)) %>%
  ggplot(aes(x = n_follower, y = max_like), na.rm = TRUE) + 
  geom_point()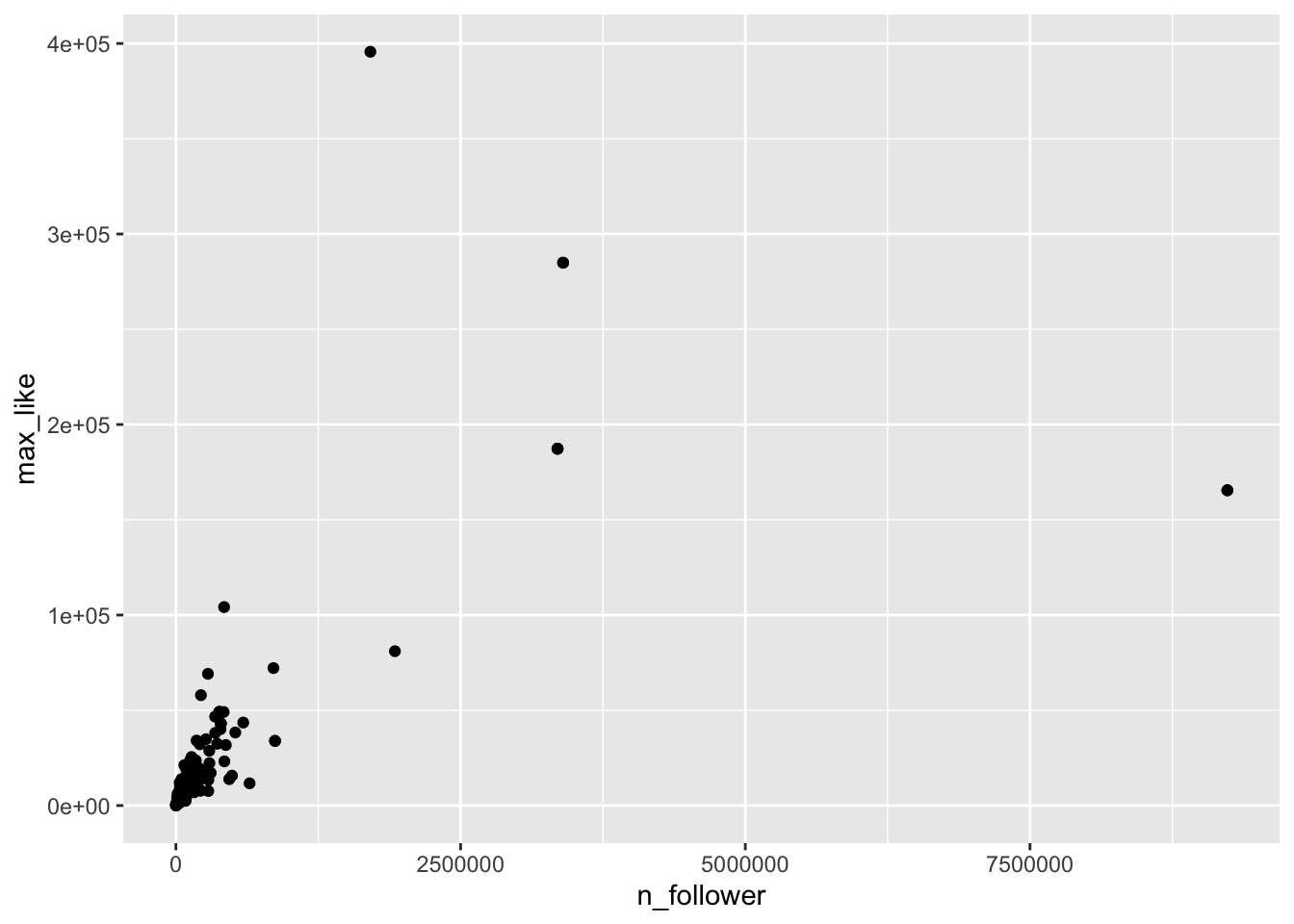

The vast majority of the athletes had small (< 10000) followings, while a few (Usain Bolt, Simone Biles, and Michael Phelps) had over 2.5 million. Even if we filter out the large followings, the graph is still badly heteroscedastic:

rio_instagram %>% 
  filter(!is.na(n_follower)) %>%
  filter(n_follower < 1000000) %>%
  ggplot(aes(x = n_follower, y = max_like), na.rm=TRUE) + 
  geom_point()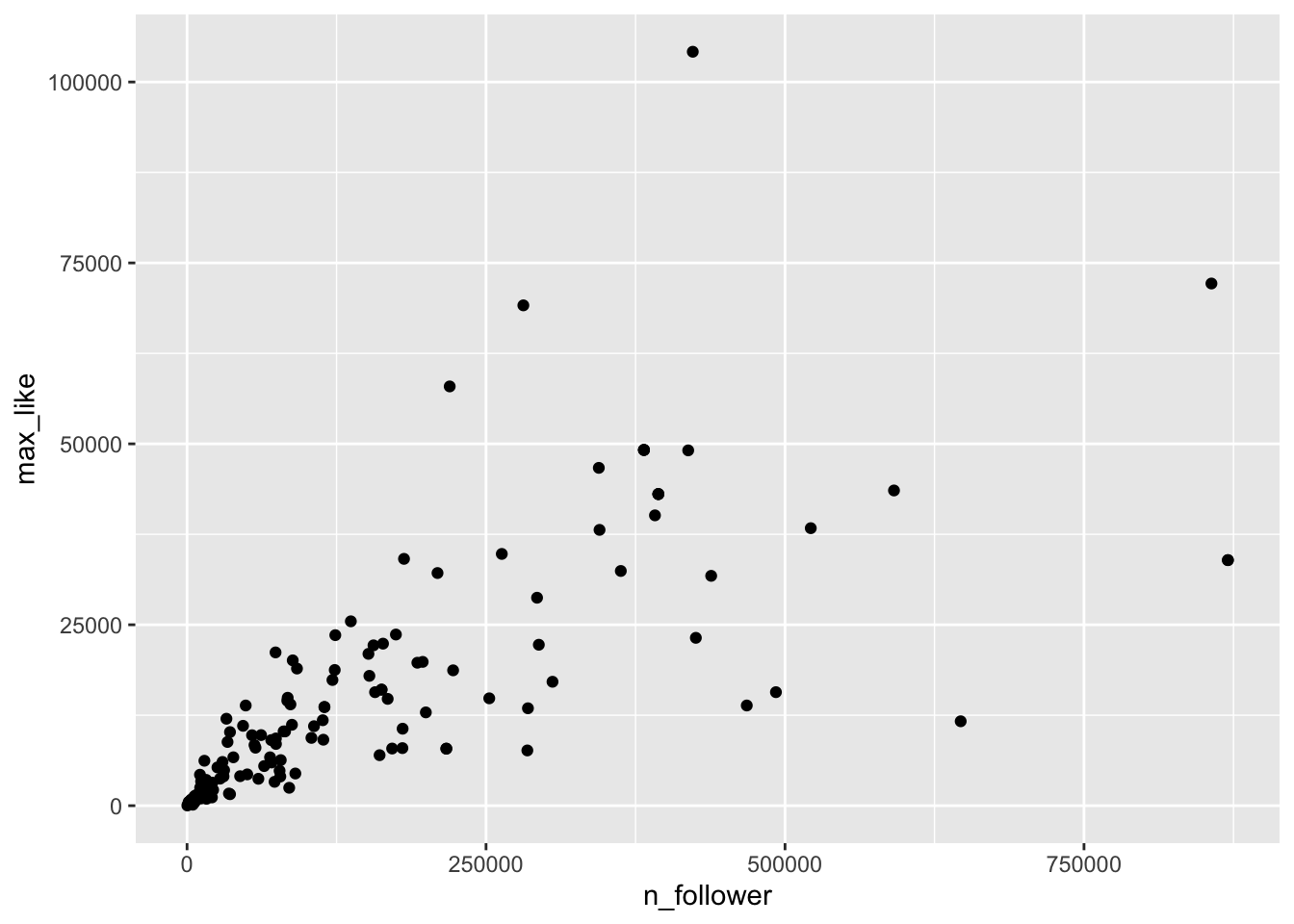

The solution is to transform the data with a logarithmic transformation. In R, the function log computes natural logarithms (base \(e\)). It is not important whether we use base 10 or natural logarithms, since they are linearly related (i.e. \(\log_e (x) = 2.303 \log_{10}(x)\)).

Here is the Rio Instagram data after applying a log transformation:

rio_instagram %>% 
  filter(!is.na(n_follower)) %>%
  ggplot(aes(x = log(n_follower), y = log(max_like)), na.rm = TRUE) +
  geom_point() + 
  geom_smooth(method = "lm")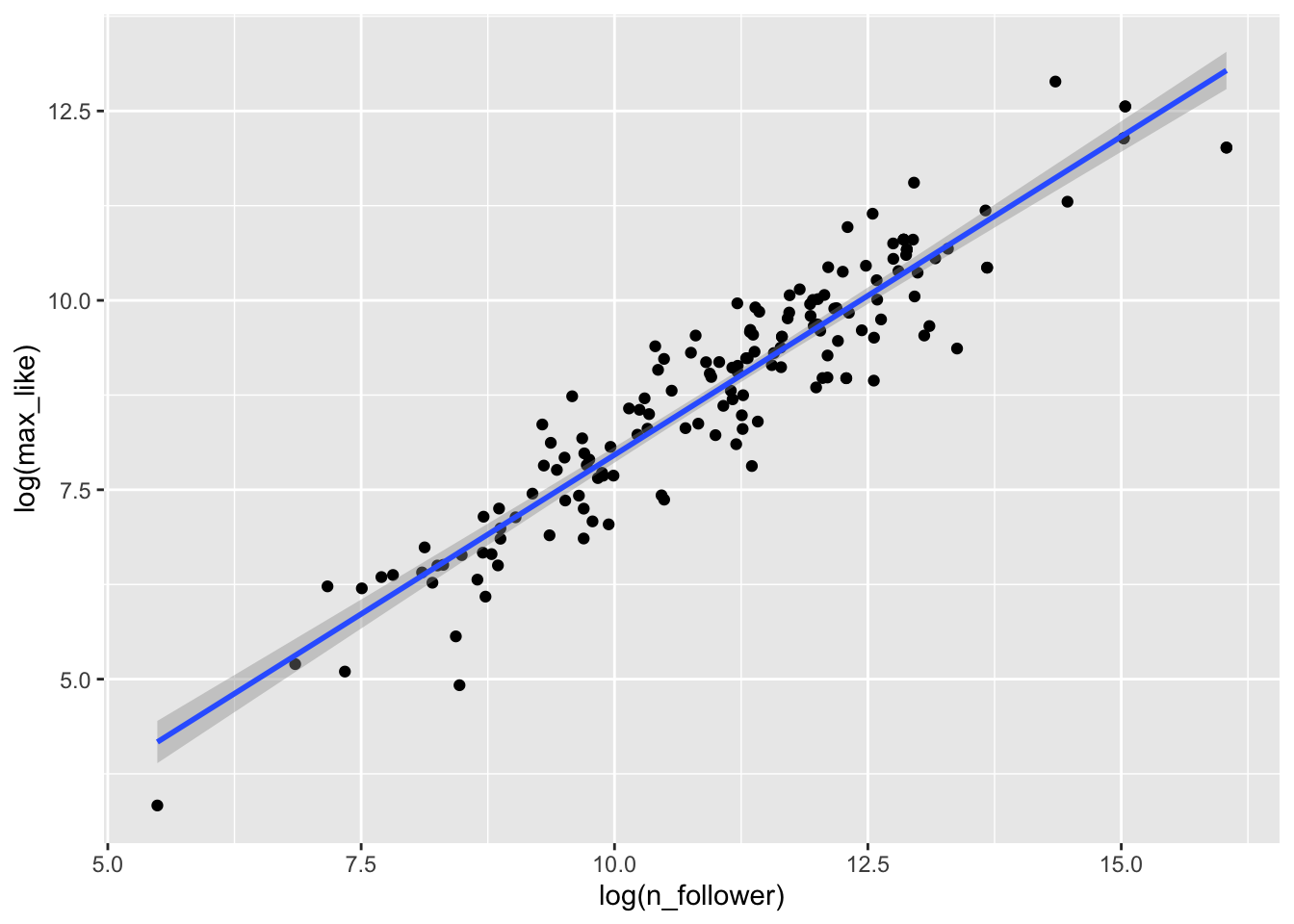

The relationship between log followers and log likes is now visibly linear, and the residuals are homoscedastic.

rio_model <- lm(log(max_like) ~ log(n_follower), data = rio_instagram)
plot(rio_model, which = 3)

rio_model$coefficients

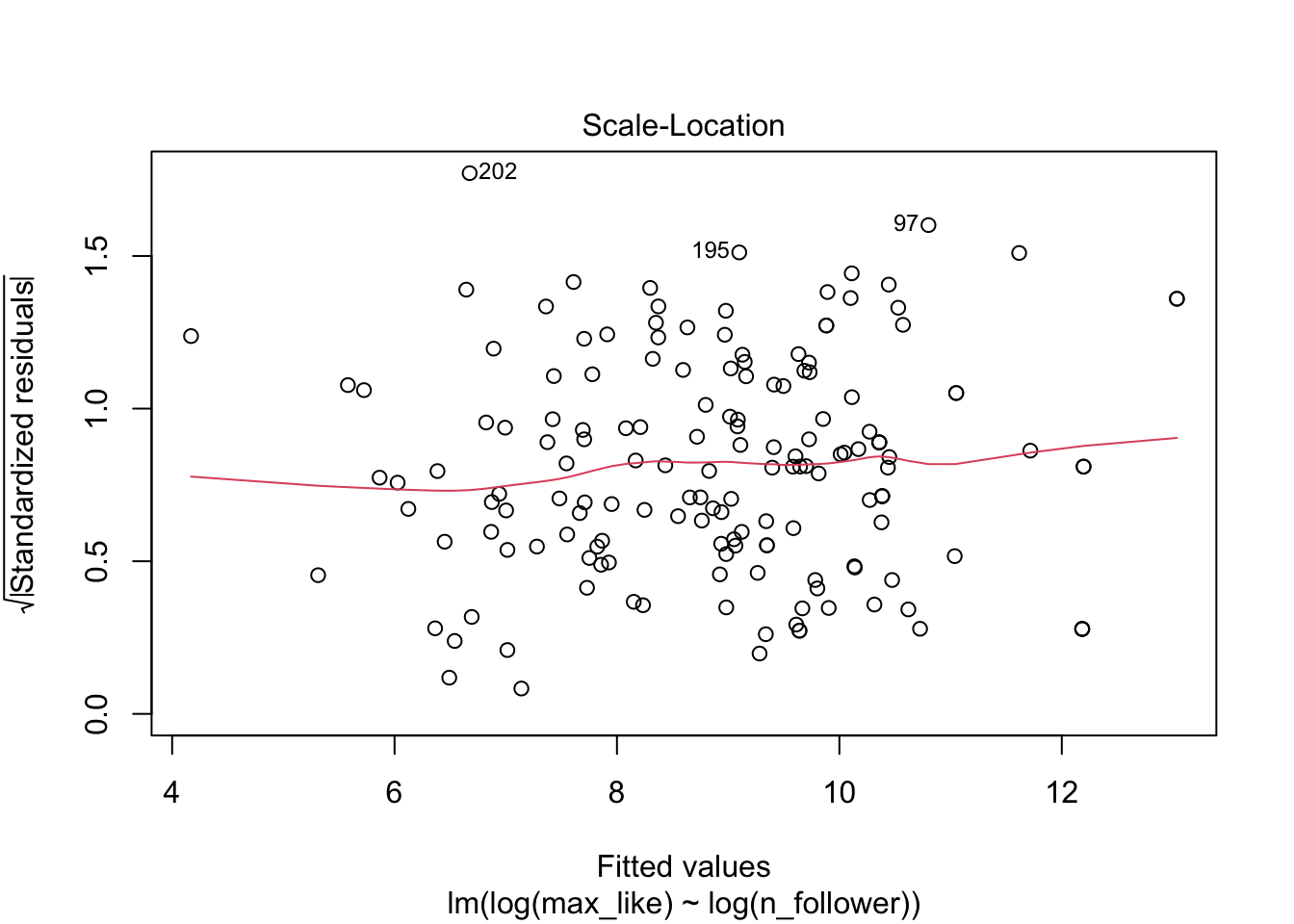
##     (Intercept) log(n_follower) 
##      -0.4430423       0.8403797

Our linear model now involves the log variables, and gives the regression line as \[ \widehat{\log(\text{Max.Likes})} = -0.443 + 0.840 \cdot \log(\text{N.follower}) \]

We can use this model to make predictions and estimates, remembering to convert to and from log scales. Alternately, we can exponentiate the regression equation to get the following relationship:

\[ \widehat{\text{Max.Likes}} = 0.642 \cdot \text{N.follower}^{0.840} \]

10.6.3 Outliers and leverage

Linear regression minimizes the SSE of the residuals. If one data point is far from the others, the residual for that point could have a major effect on the SSE and therefore the regression line. A data point which is distant from the rest of the data is called an outlier.

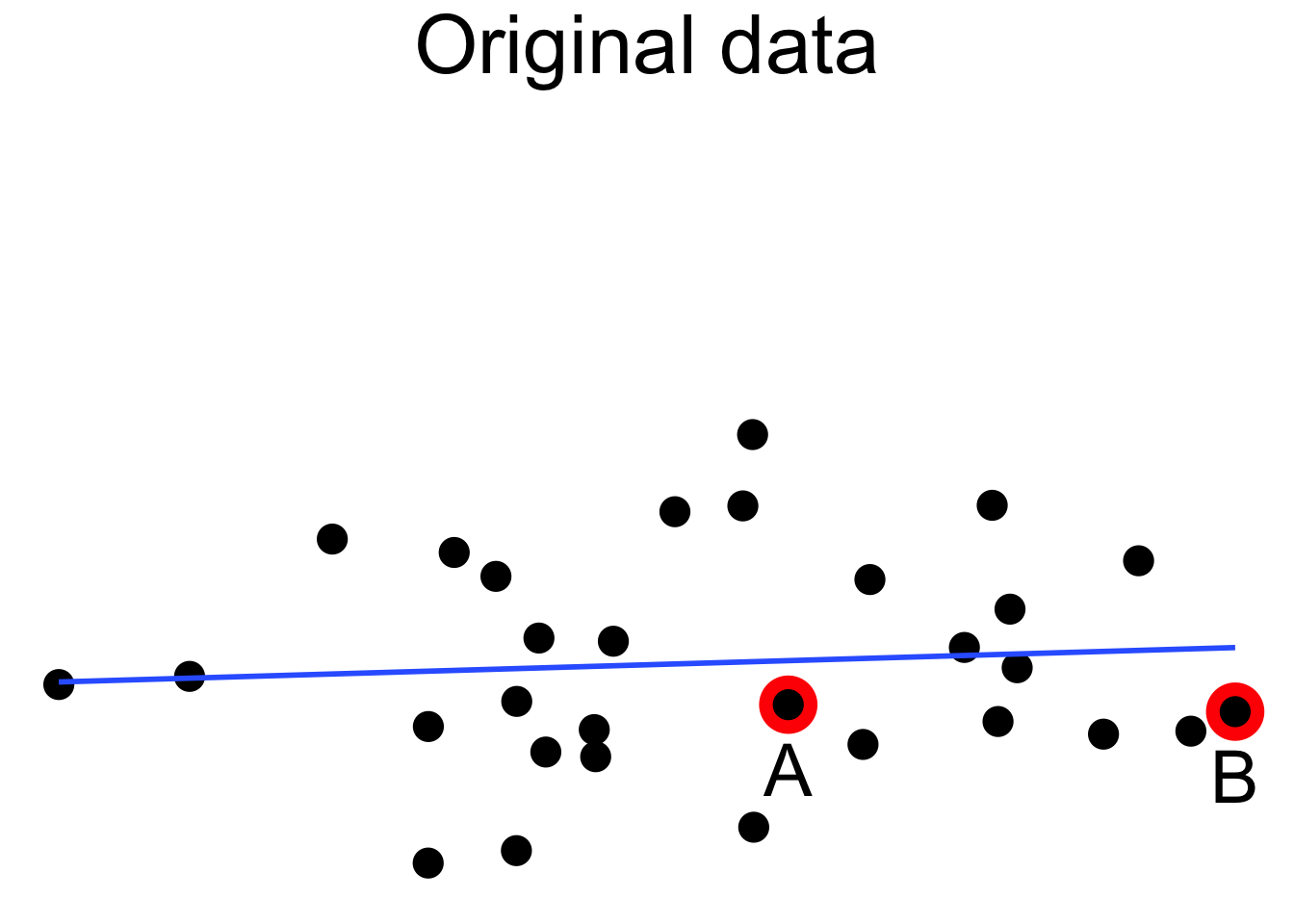
Outliers can pull the regression line towards themselves. The regression line always goes through the center of mass of the data, the point \((\bar{x},\bar{y})\). If the outlier’s \(x\) coordinate is far from the other \(x\) coordinates in the data, then a small pivot of the line about the center of mass will make a large difference to the residual for the outlier. Because the outlier contributes the largest residual, it can have an outsized effect on the slope of the line. This phenomenon is called leverage

Here we see a cloud of uncorrelated points, with two labeled \(A\) and \(B\). Point \(A\) has an \(x\) coordinate close to the mean \(x\) coordinate of all points, so changing its \(y\) value has a small effect on the regression line. This is shown in the second picture. Point \(B\) has an \(x\) coordinate that is extreme, and the third picture shows that changing its \(y\) value makes a large difference to the slope of the line. Point \(A\) has low leverage, point \(B\) has high leverage.

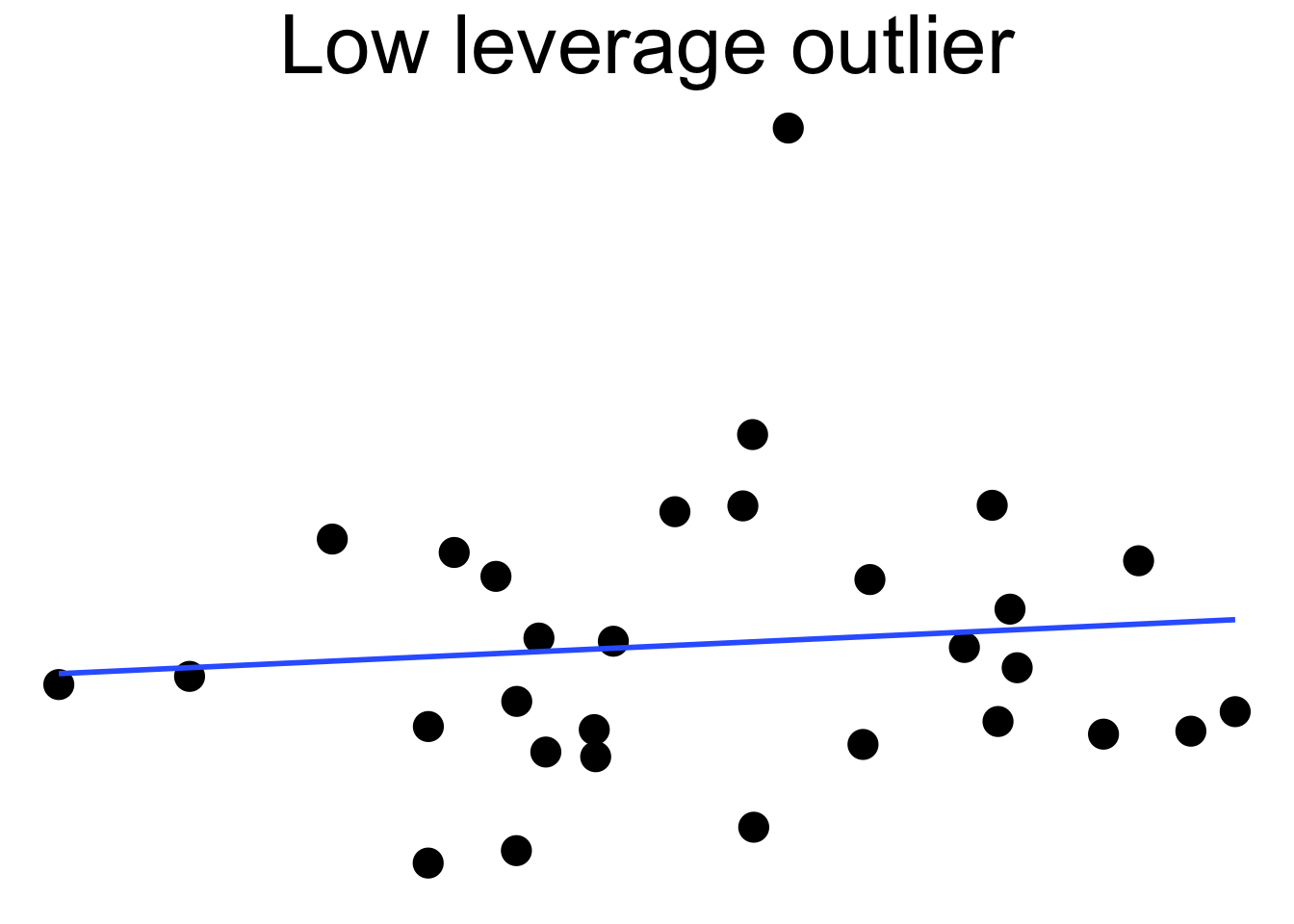
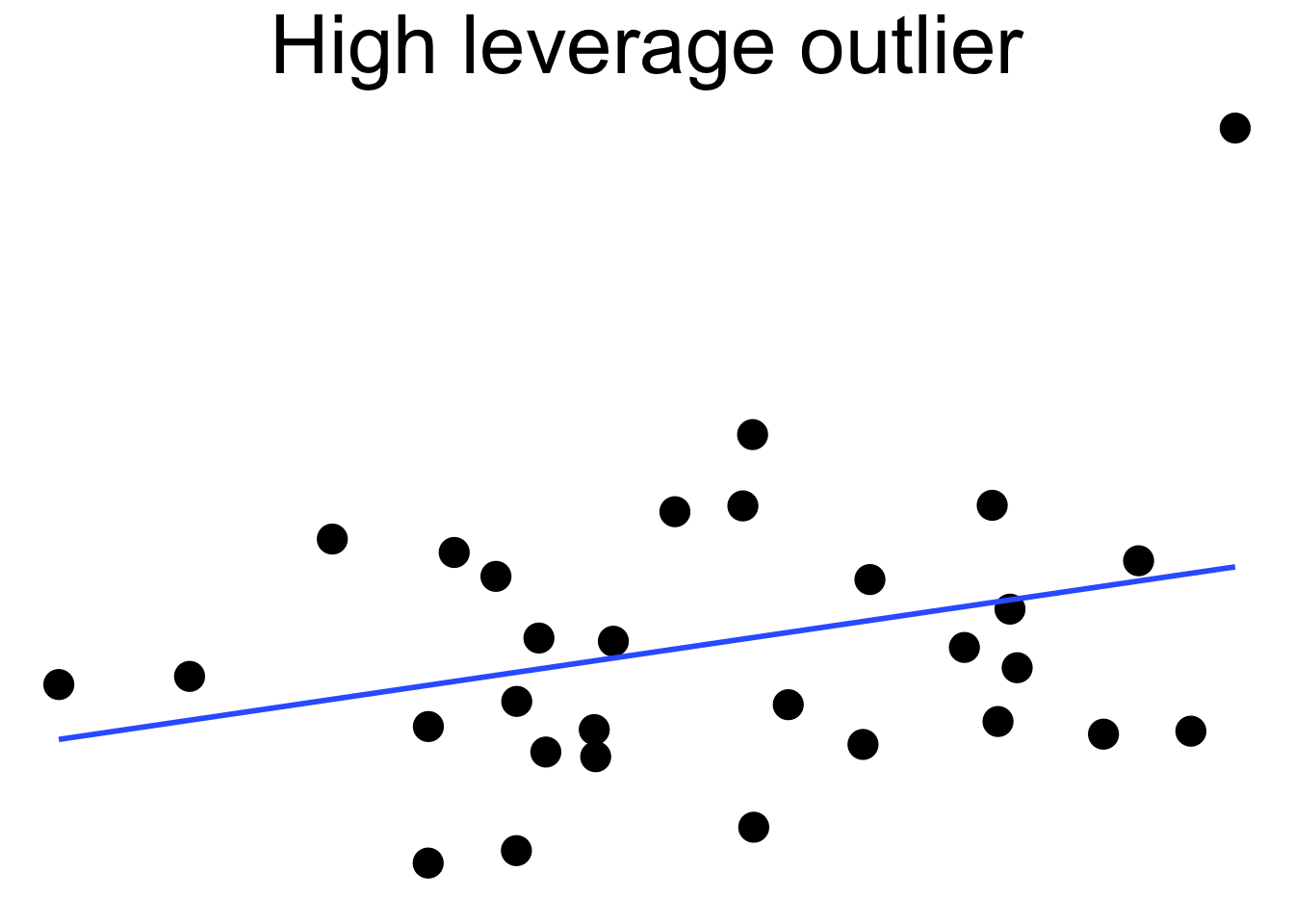
Dealing with high leverage outliers is a challenge. Usually it is a good idea to run the analysis both with and without the outliers, to see how large of an effect they have on the conclusions. A more sophisticated approach is to use robust methods. Robust methods for regression are analogous to rank based tests in that both are resistant to outliers. However, robust regression is outside the scope of this text.

Example The pulitzer³⁵ data contains data on the circulation of fifty major U.S. newspapers along with counts of the number of Pulitzer prizes won by each. Do Pulitzer prizes help newspapers maintain circulation?

We plot the number of Pulitzer prizes won as the explanatory variable, and the percent change in circulation from 2004-2013 as the response. The pulitzer data is available in the fivethirtyeight package.

pulitzer <- fivethirtyeight::pulitzer
pulitzer <- rename(pulitzer, pulitzers = num_finals2004_2014)
ggplot(pulitzer, aes(x = pulitzers, y = pctchg_circ)) + 
  geom_point() + 
  geom_smooth(method = "lm")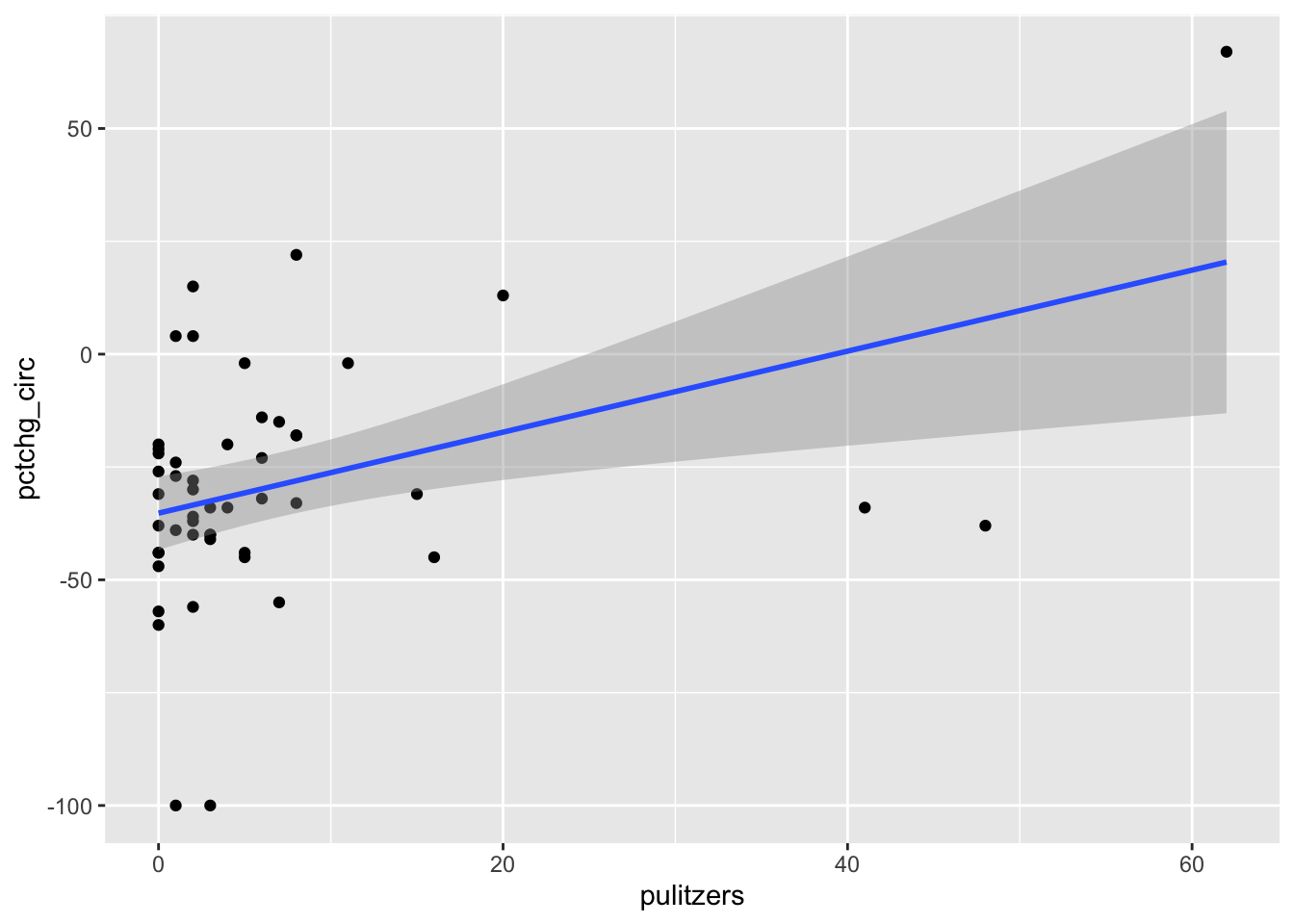

The regression line has positive slope, suggesting that that more Pulitzer prizes correspond with an increase (or smaller decrease) in circulation. There are some high leverage outliers with a large number of Pulitzers compared to the other newspapers. To handle this, perform the regression with and without the outliers, and see if it makes a difference.

For the full data set, test the hypothesis that the slope is non-zero:

pulitzer_full_model <- lm(pctchg_circ ~ pulitzers, data = pulitzer)
summary(pulitzer_full_model)

## 
## Call:
## lm(formula = pctchg_circ ~ pulitzers, data = pulitzer)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -67.462  -9.115  -2.257  12.833  50.051 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -35.2299     4.0560  -8.686 2.07e-11 ***
## pulitzers     0.8973     0.2945   3.047  0.00376 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 25.03 on 48 degrees of freedom
## Multiple R-squared:  0.162,  Adjusted R-squared:  0.1446 
## F-statistic: 9.281 on 1 and 48 DF,  p-value: 0.003755

The correlation between Pulitzers and circulation change is significant (\(p = 0.00376\)). The correlation coefficient \(r = \sqrt{0.162} = 0.402\), which is reasonably large.

The high leverage outliers show up in the “Residuals vs Leverage” diagnostic plot

plot(pulitzer_full_model, which = 5)

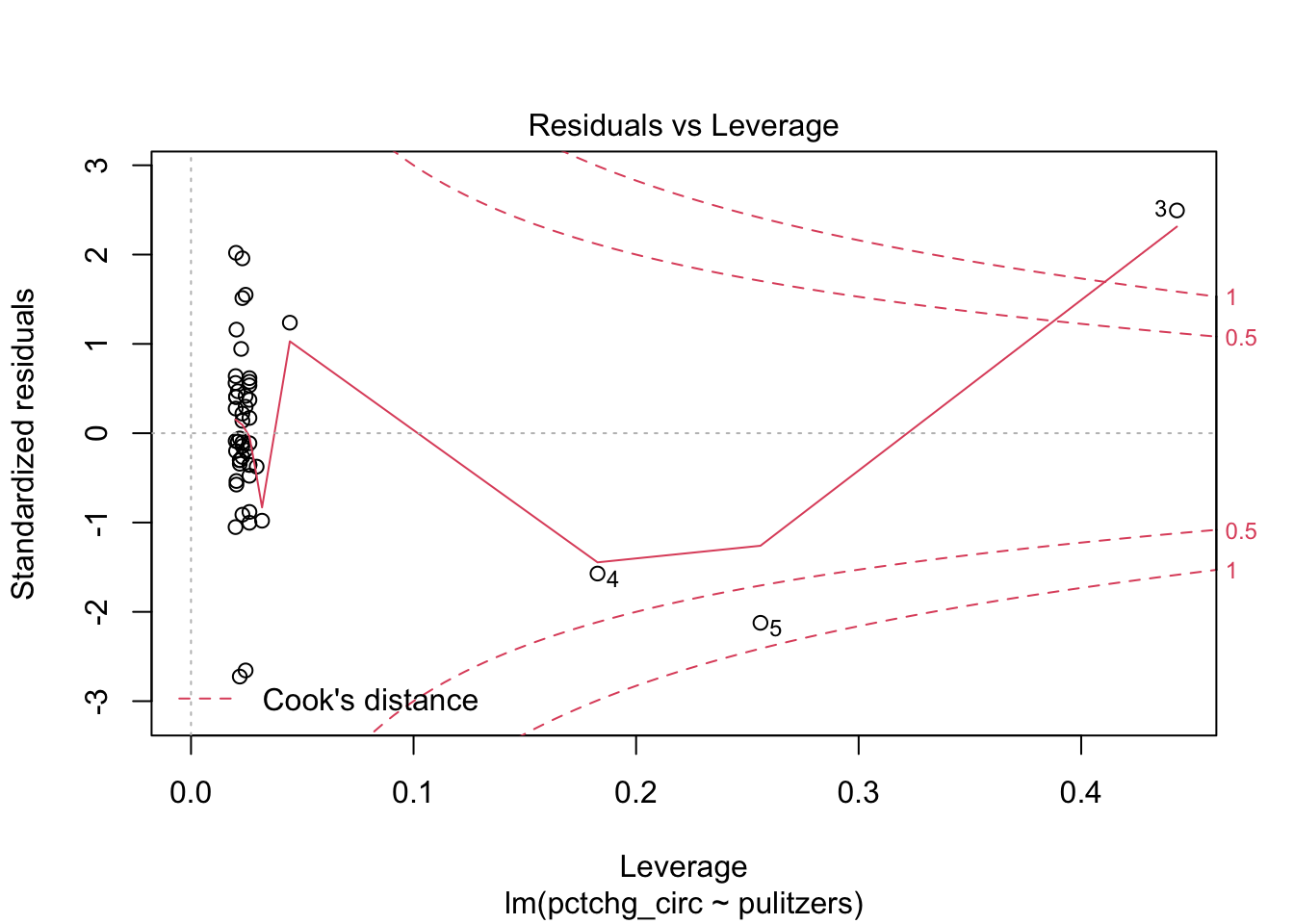
Newspaper 3 is well outside the red “Cook’s distance” lines.. What paper is it?

pulitzer$newspaper[3]

## [1] "New York Times"

Now consider the same hypothesis test, but remove the New York Times:

pulitzer_trimmed_model <- pulitzer %>%
  filter(newspaper != "New York Times") %>%
  lm(pctchg_circ ~ pulitzers, data = .)
summary(pulitzer_trimmed_model)$coefficients

##                Estimate Std. Error    t value     Pr(>|t|)
## (Intercept) -32.6010955   3.951176 -8.2509857 1.077854e-10
## pulitzers     0.2571302   0.368351  0.6980576 4.885806e-01

The slope is no longer significantly different from zero (\(p = 0.489\)), and the correlation coefficient is now only 0.1.

The apparent correlation between Pulitzer prizes and circulation is almost entirely due to the New York Times. Because most newspapers are struggling and the New York Times is one of the few that are not, it is hard to say if quality (as measured by prizes) does influence circulation. As always, correlation is not causation, and here even the correlation itself is questionable.

As with all real problems, statistical analysis can only inform actions taken, and is not a conclusion in itself. As a newspaper publisher, how would you use this data? It is possible that emulating the New York Times would be a good strategy.

10.7 Simulations

10.7.1 Residuals

It can be tricky to learn what “good” residuals look like. One of the nice things about simulated data is that you can train your eye to spot departures from the hypotheses. Let’s look at two examples: one that satisfies the regression assumptions and one that does not. You should think about other examples you could come up with!

Example 10.1 Consider simulated data that follows the model \(y_i = 2 + 3x_i + \epsilon_i\), where \(\epsilon_i\) is iid normal with mean 0 and standard deviation 5. This model satisfies the assumptions required for linear regression, so it an example of good behavior.

x <- runif(40, 10, 20) # 40 explanatory values between 10 and 20
epsilon <- rnorm(40, 0, 5)  # 40 error terms, normally distributed
y <- 2 + 3 * x + epsilon
my_model <- lm(y ~ x)
my_model$coefficients

## (Intercept)           x 
##     5.77620     2.77251

The estimate for the intercept is \({\hat\beta}_0=\) 5.7762 and for the slope it is \({\hat\beta}_1=\) 2.77251. The estimated slope is close to the true value of 3. The estimated intercept is less accurate because the intercept is far from the data, at \(x=0\), and so small changes to the line have a large effect on the intercept.

Printing the full summary of the model gives the residual standard error as 4.17229. The the true standard deviation of the error terms \(\epsilon_i\) was chosen to be 5, so the model’s estimate is good.

data.frame(x, y) %>% ggplot(aes(x = x, y = y)) +
  geom_point() + geom_smooth(method = "lm")
plot(my_model, which=1)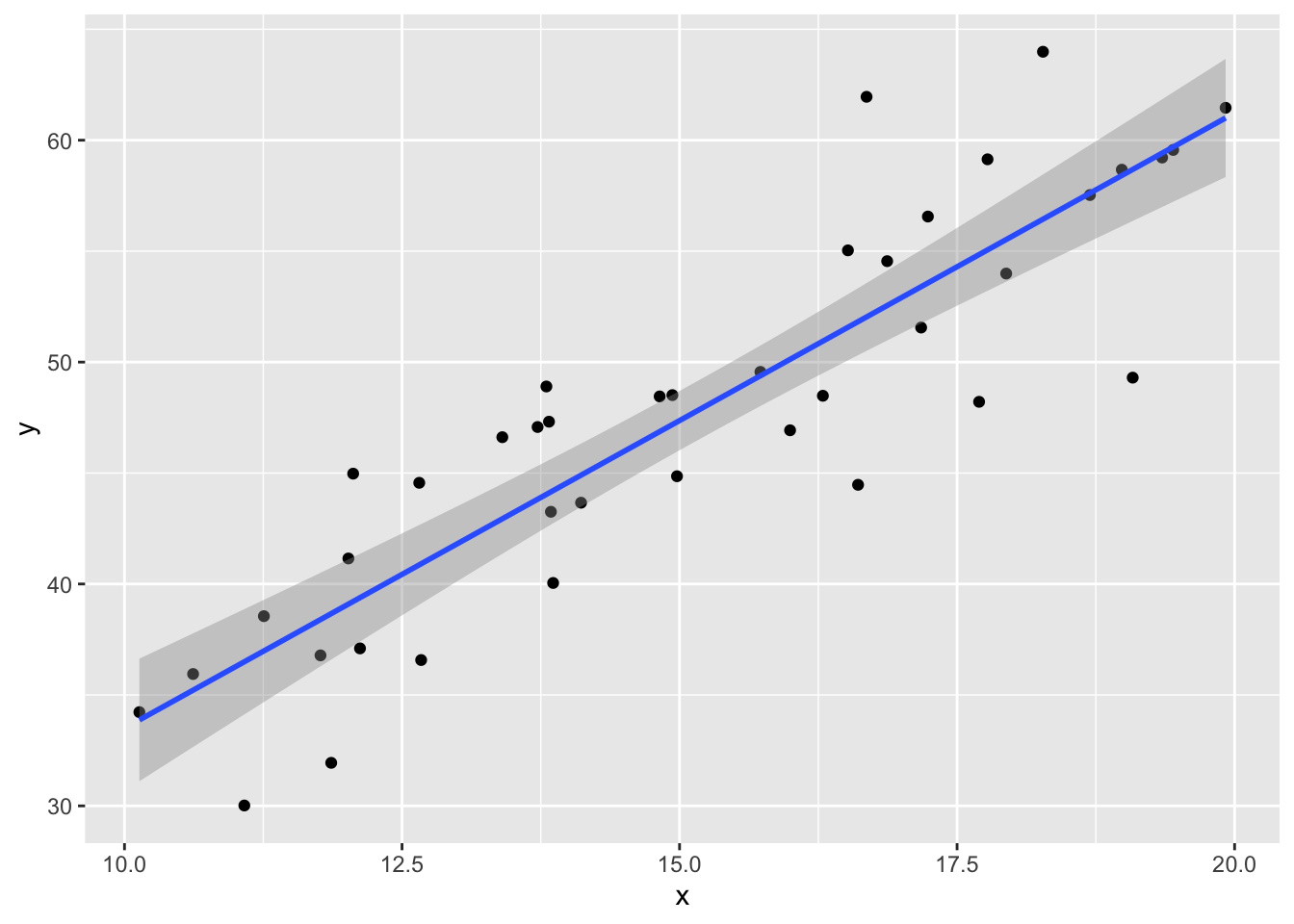

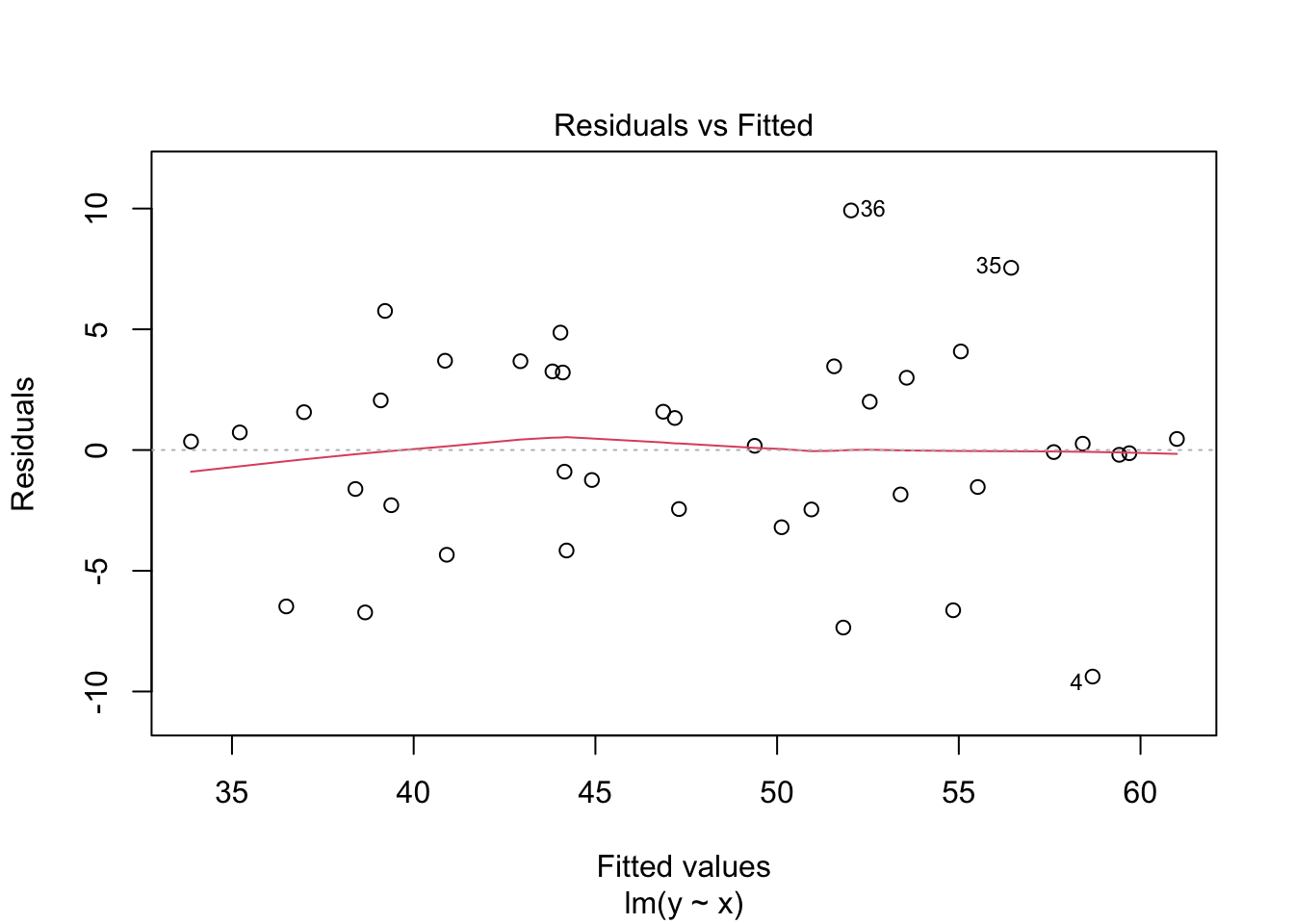
The regression line follows the line of the points and the residuals are more or less symmetric about 0.

Example 10.2 What happens if the errors in a regression model are non-normal? The data no longer satisfies the hypothesis needed for regression, but how does that affect the results?

This example shows the effect of skew residuals. As in Example 10.1, \(y_i = 2 + 3x_i + \epsilon_i\) except that we now use iid exponential with rate 1/10 for the error terms \(\epsilon_i\), and subtract 5 so that the error terms still have mean 0.

x <- runif(40, 10, 20) # 40 explanatory values between 10 and 20
epsilon <- rexp(40, 1/10) - 5  # 40 error terms, mean 0 and very skew
y <- 2 + 3 * x + epsilon
my_model <- lm(y ~ x)
my_model$coefficients

## (Intercept)           x 
##   18.877888    2.284571

The estimate for slope is fairly close to the true value of 3, but the intercept is far from 2.

data.frame(x, y) %>% ggplot(aes(x = x, y = y)) +
  geom_point() + geom_smooth(method = "lm")
plot(my_model, which=1)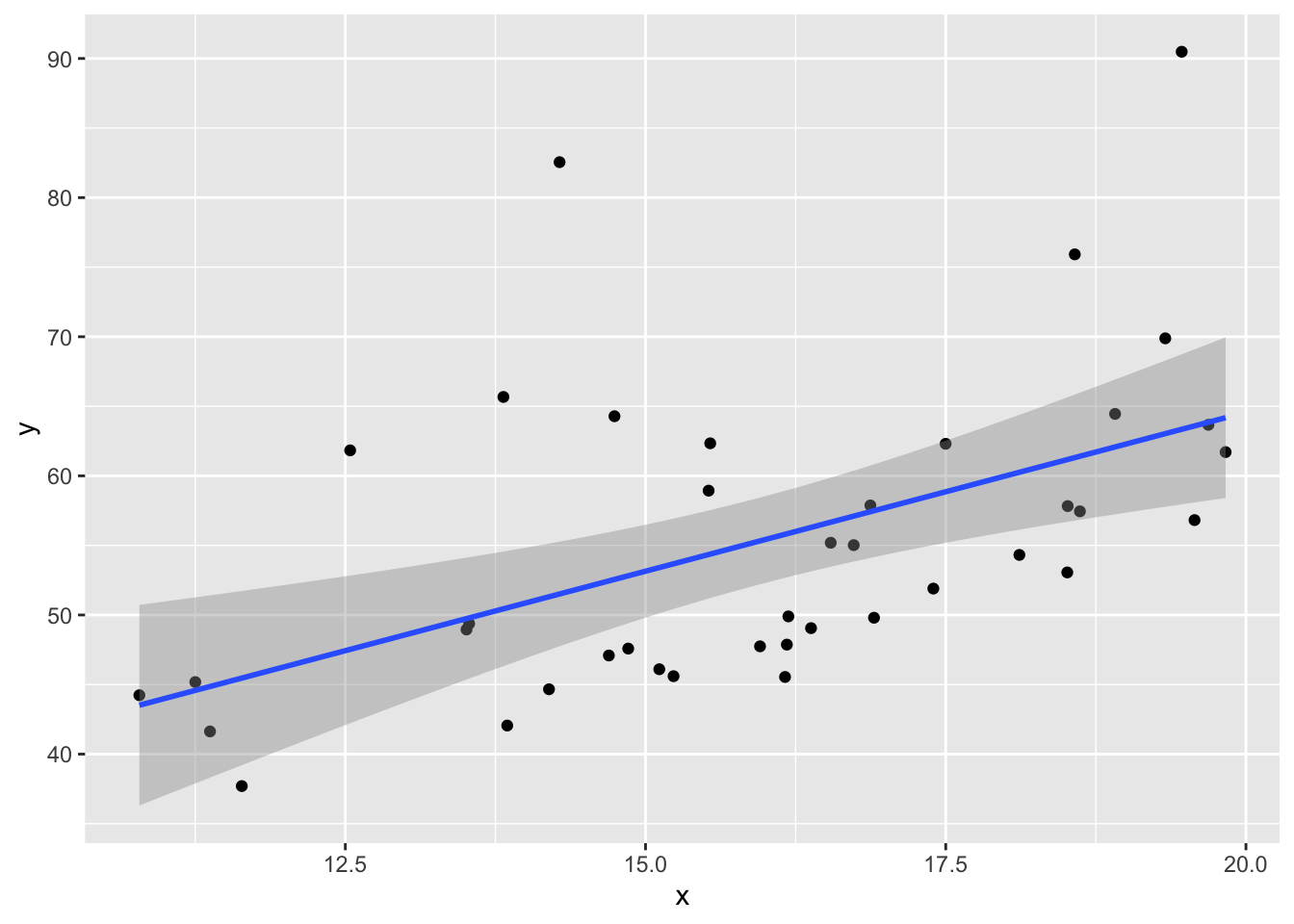

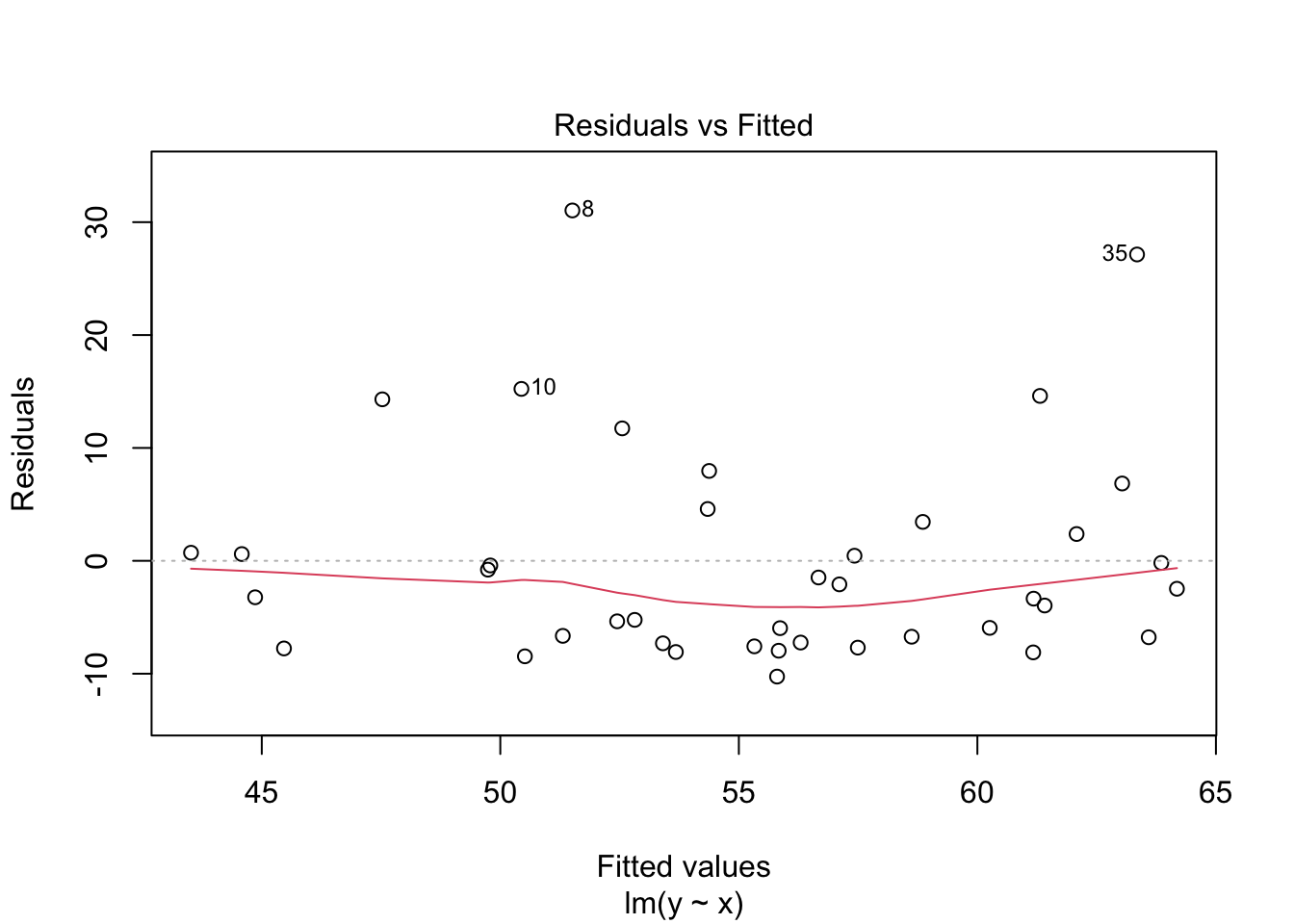
In the residuals plot, the residuals are larger above the zero line than below it, displaying the skewness of the residuals. The skew is even more apparent in the Normal Q-Q plot as an upward curve:

plot(my_model, which=2)

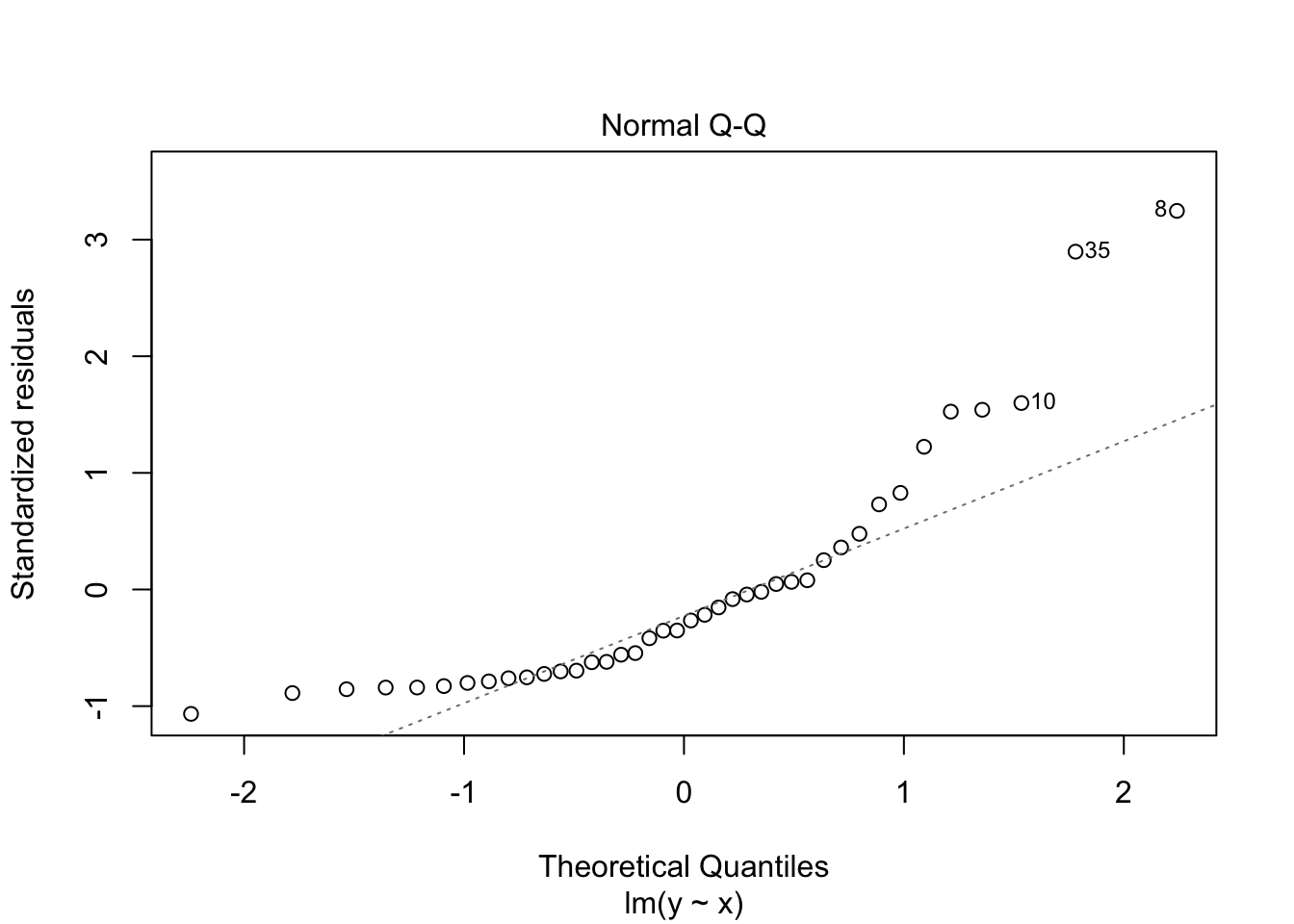
10.7.2 Prediction intervals

In this section, we explore prediction intervals through simulation. We will find that a small error in modeling has minimal effect near the center of our data range, but can lead to large errors near the edge of observed data. Beyond the data’s edge, making predictions is called extrapolation and can be wildly incorrect.

We will compare the behavior of prediction intervals for two sets of simulated data:

Data 1 (linear, assumptions correct): \(y_i = 1 + 2x_i + \epsilon_i\)
Data 2 (non-linear, assumptions incorrect): \(y = 1 + 2x_i + x^2/20 + \epsilon_i\)

In both sets, the error terms \(\epsilon_i \sim \text{Norm}(0,1)\) and there are 20 \(x\) values uniformly randomly distributed on the interval \((0,10)\).

simdata <- data.frame(x = runif(20,0,10),epsilon = rnorm(20))
simdata <- mutate(simdata, y1 = 1 + 2 * x + epsilon,
                   y2 = 1 + 2 * x + x^2/20 + epsilon)

Data 1 meets the assumptions for linear regression, because the relationship between explanatory and response variables is linear and the error terms are iid normal. Data 2 does not meet the assumptions for linear regression, because the relationship between the variables is non-linear: there is a small quadratic term \(x^2/20\).

Compare the two sets of simulated data visually:

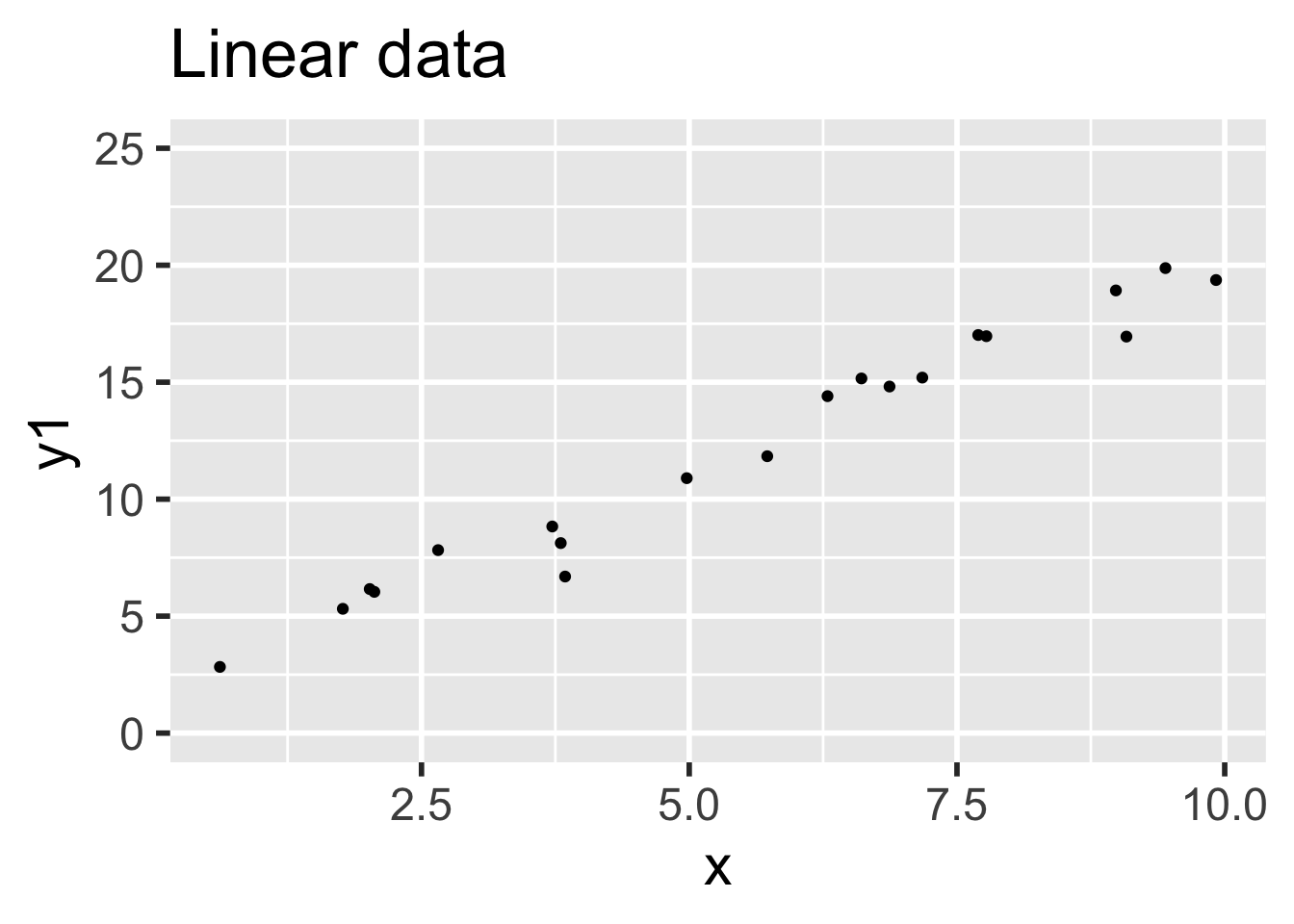
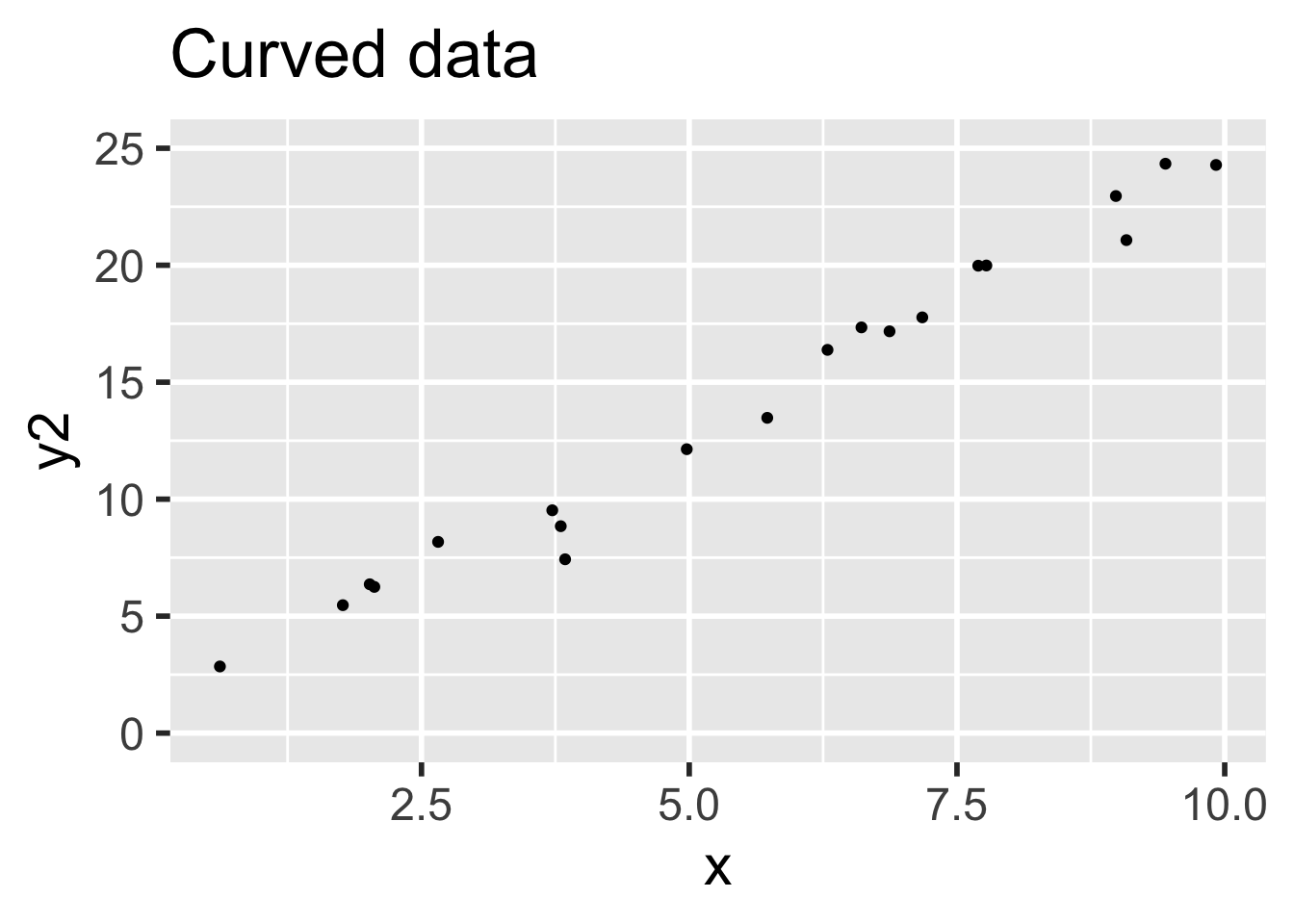
It is easy to believe that the quadratic term in the second set of data might go unnoticed.

Next, compute the 95% prediction intervals for both data sets at \(x = 5\). We use a linear model in both cases, even though the linear model is not correct for the non-linear data.

model1 <- lm(y1 ~ x, data = simdata)
predict(model1, newdata = data.frame(x = 5), interval = "pre")

##        fit      lwr      upr
## 1 11.14539 9.158465 13.13232

model2 <- lm(y2 ~ x, data = simdata)
predict(model2, newdata = data.frame(x = 5), interval = "pre")

##        fit     lwr      upr
## 1 12.77723 10.7008 14.85366

The two prediction intervals are quite similar. In order to test whether the prediction interval is working correctly, we need to repeatedly create sample data, apply lm, create a new data point, and see whether the new data point falls in the prediction interval. We do this for the linear data first:

trials <- replicate(10000, {
  # generate data
  simdata <- data.frame(x = runif(20, 0, 10), epsilon = rnorm(20))
  simdata <- mutate(simdata, y1 = 1 + 2 * x + epsilon)
  
  # create a new data point at a random x location
  new_x <- runif(1,0,10)
  new_y <- 1 + 2 * new_x + rnorm(1)

  # build the prediction interval at x = new_x
  model1 <- lm(y1 ~ x, data = simdata)
  predictint <- predict(model1, newdata = data.frame(x = new_x), interval = "pre")
  
  # test if the new data point's y-value lies in the prediction interval
  predictint[2] < new_y && new_y < predictint[3]
})
mean(trials)

## [1] 0.9499

We find that the 95% prediction interval successfully contained the new point 94.99% of the time. That’s pretty good! Repeating the simulation for the curved data, the 95% prediction interval is successful about 94.8% of the time, which is also quite good.

However, let’s examine things more carefully. Instead of picking our new data point at a random \(x\) coordinate, let’s always choose \(x = 10\), the edge of our data range.

trials <- replicate(10000, {
  # generate data
  simdata <- data.frame(x = runif(20, 0, 10), epsilon = rnorm(20))
  simdata <- mutate(simdata, y2 = 1 + 2 * x + x^2/20 + epsilon)
  
  # create a new data point at x=10
  new_x <- 10
  new_y <- 1 + 2 * new_x + new_x^2/20 + rnorm(1)

  # build the prediction interval at x = 10
  model2 <- lm(y2 ~ x, data = simdata)
  predictint <- predict(model2, newdata = data.frame(x = 10), interval = "pre")
  
  # test if the new data point's y-value lies in the prediction interval
  predictint[2] < new_y && new_y < predictint[3]
})
mean(trials)

## [1] 0.9029

The prediction interval is only correct 90.29% of the time. This isn’t working well at all!

For the curved data, the regression assumptions are not met. The prediction intervals are behaving as designed for most of the \(x\) values, but fail twice as often as they should at \(x = 10\).

When making predictions, be careful near the bounds of the observed data. Things get even worse as you move \(x\) further from the known points. A statistician needs strong evidence that a model is truly linear to perform extrapolation.

Vignette: Simple Logistic Regression

Regression is a very large topic, and one can do many, many more things than what we discussed in this chapter. One common task is to model the probability of an event occurring based on one or more predictor variables. For this, we can use logistic regression. In this vignette, we model use the data set malaria³⁶ in the fosdata package to model the probability that a mouse will contract malaria on the number of sporozoite parasites detected in the mosquitoe’s salivary glands.

Let \(Y\) be a random variable that takes on the value 1 if the mouse contracts malaria, and 0 if not. A first thought for a model might be \(P(Y = 1) = \beta_0 + \beta_1 x\), where \(x\) is the number of sporozoites. This type of model can be appropriate, but we also see that it can easily lead to probabilities that are bigger than 1 or less than 0. In logistic regression, we have the model (where \(p = P(Y = 1)\)) \[ \log \frac{p}{1-p} = \beta_0 + \beta_1 x, \] or equivalently, \(p = \frac{e^{\beta_0 + \beta_1 x}}{1 + e^{\beta_0 + \beta_1 x}}\).

How to interpret this? Well, \(\frac{p}{1-p}\) is the odds of the event occurring, so \(\log \frac{p}{1-p}\) is the log odds of it occurring. If the log-odds are a big positive number, then it is very likely for the event to occur. If they are zero, then it is 50-50, and a big negative number corresponds to very unlikely for an event to occur. We are modeling these log-odds as an affine combination of the predictor variable.

There are several ways of estimating \(\beta_0\) and \(\beta_1\). However, we will not go over the details except to say that they are implemented in the R function glm. We can find estimates for \(\beta_0\) and \(\beta_1\) via

malaria <- fosdata::malaria
malaria_mod <- glm(malaria ~ sporozoite, family = "binomial", data = malaria)
broom::tidy(malaria_mod)

## # A tibble: 2 x 5
##   term        estimate std.error statistic  p.value
##   <chr>          <dbl>     <dbl>     <dbl>    <dbl>
## 1 (Intercept)   -2.48     0.428      -5.79 7.07e- 9
## 2 sporozoite     0.462    0.0645      7.17 7.74e-13

We see that the estimate for \(\beta_0\) is -2.4761526 and the estimate for \(\beta_1\) is 0.4622328. The value for the slope is significant at the \(\alpha = .05\) level. Let’s look at a plot.

ggplot(malaria, aes(x = sporozoite, y = malaria)) +
  geom_jitter(height = 0, width = 0.2) + 
  geom_smooth(method = "glm",  
              method.args=list(family="binomial"), 
              se=FALSE)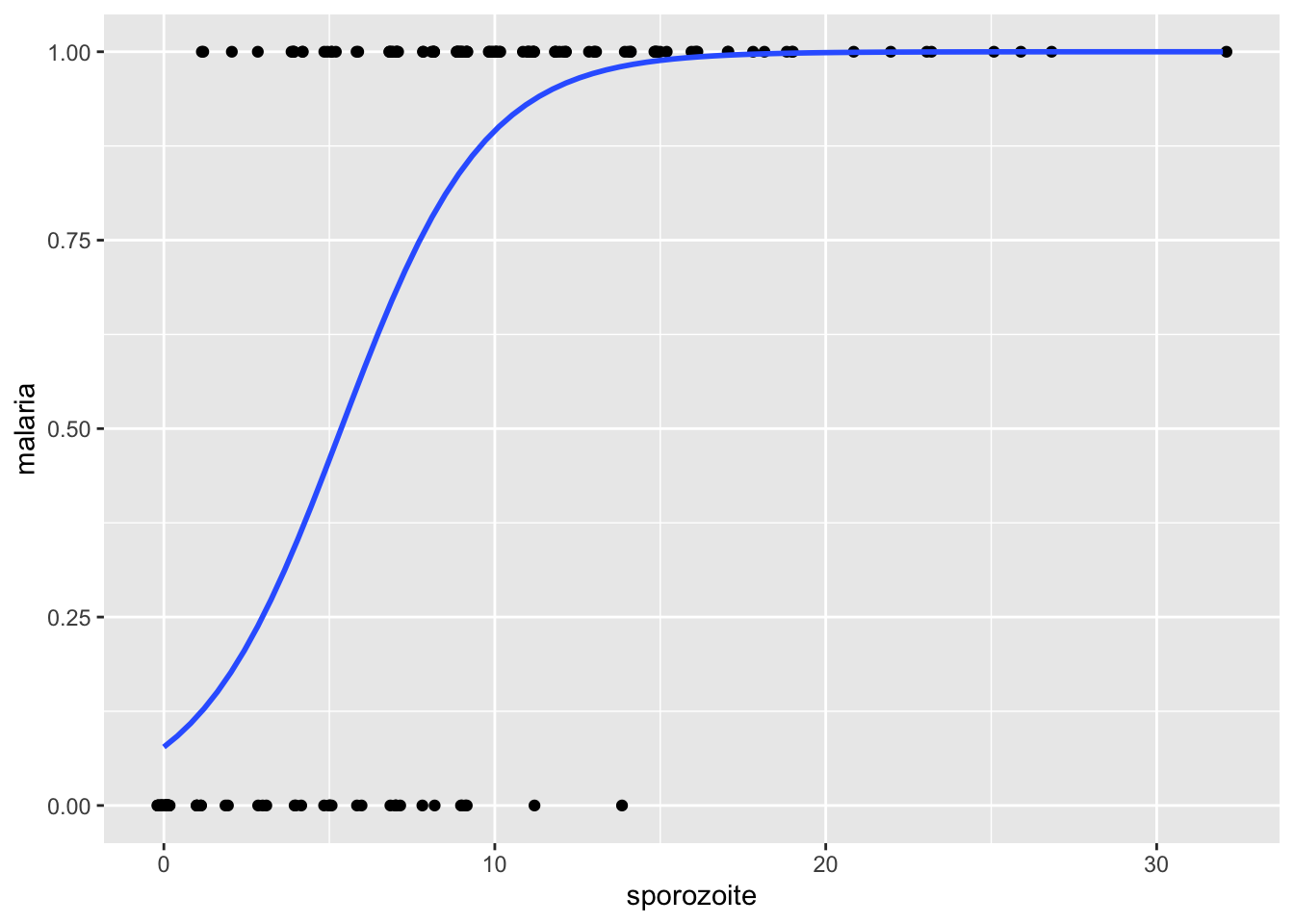

The blue curve is the estimate of the probability of contracting malaria based on the total number of sporozoites. We can see that when there are zero sporozoites, the model predicts a low probability of contracting malaria. When there are more than 20, then the probability is essentially 1. There is much more to logistic regression than what we have shown in this vignette. We hope this taste of it will encourage you to further study!

Exercises

The built-in data set faithful gives data on eruptions of the Old Faithful geyser in Yellowstone National Park. Each observation has a length of time the eruption lasted (eruptions) and the length of time until the next eruption (waiting), both in minutes.
1. Find the equation of the regression line to explain waiting as a function of eruptions.
2. Plot the data and the regression line.
3. How long do you expect to wait after a 4.3 minute eruption?
Consider the data set crit_period in the fosdata package. The critical period hypothesis posits that there is a critical period (young) for first exposure to a second language, and that first exposure past the critical period makes it much more difficult to attain high levels of second language proficiency.
1. Consider the North American subjects only, and plot gjt (scores on the grammaticality judgment test) versus aoa (age of onset of acquisition).
2. Find the coefficients of the regression line and plot it on top of the scatterplot.
3. What does the slope represent in terms of this data?
4. Examine the residuals. The critical period hypothesis predicts that there will be an elbow shape or L shape in the residuals versus fitted. Do you see that in your residuals?
Consider the juul data set in ISwR.
1. Fit a linear model to explain igf1 level by age for people under age 20 who are in tanner puberty group 5.
2. Give the equation of the regression line and interpret the slope in terms of age and igf1 level.
3. Predict the igf1 level of a 16 year old who is in tanner puberty group 5.
The data set hot_dogs is in the fosdata package. (Original Source: SOCR 012708 Consumer Reports, 1986.)
1. Make a scatterplot showing Sodium content as a function of Calories. Color your points using the hot dog Type.
2. Remove the Poultry hot dogs (why?) and then construct a linear model to explain Sodium content as a function of Calories. What is the equation of your regression line?
3. How much Sodium does your model predict for a 140 Calorie Beef or Meat hot dog?
4. Give the prediction interval that contains the sodium level for 95% of 140 Calorie Beef or Meat hot dogs.
The data set engel contains data on income and food expenditure for 235 working class Belgian households. To load this data, load the quantreg package and then enter the command data(engel).
1. Make a plot of foodexp as explained by income and show the regression line on your plot.
2. Compute the linear model and plot the residuals.
3. The assumptions for linear regression are not satisfied. What is wrong with the residuals?
Consider the Batting data from the Lahman data set. This problem uses home runs (HR) to explain total runs scored (R) in a baseball season.
1. Construct a data frame that has the total number of HR hit and the total number of R scored for each year in the data set.
2. Create a scatterplot of the data, with HR as the explanatory variable and R as the response. Use color to show the yearID.
3. Notice early years follow a different pattern than more modern years. Restrict the data to the years from 1970 to the present, and create a new scatterplot.
4. Fit a linear model to the recent data. How many additional R does the model predict for each additional HR? Is the slope significant?
5. Plot the best-fit line and the recent data on the same graph.
6. Create a prediction interval for the total number of runs scored in the league if a total of 4000 home runs are hit. Would this be a valid prediction interval if we found new data for 1870 that included HR but not R?
Consider the data set Anscombe, which is in the carData package. (Note: do not use the data set anscombe, which is preloaded in R.) The data contains, for each U.S. state, the per capita education expenditures (education) and the number of youth per 1000 people (young).
1. Would you expect number of youth and per capita education expenditures to be correlated? Why or why not?
2. What is the correlation coefficient between number of youth and per capita education expenditures?
3. Model expenditures as a function of number of youth. Interpret the slope of the regression line. Is it significant?
4. Examine your data and residuals carefully. Model the data minus the one outlier, and re-interpret your conclusions in light of this.
Consider the ex0728 data set in Sleuth2 (note: not in Sleuth3!). This gives the year of completion, height and number of stories for 60 randomly selected notable tall buildings in North America.
1. Create a scatterplot of Height (response) versus Stories (explanatory).
2. Which building(s) are unexpectedly tall for their number of stories?
3. Is there evidence to suggest that the height per story has changed over time?
Consider the data in ex0823 in Sleuth3. This data set gives the wine consumption (liters per person per year) and heart disease mortality rates (deaths per 1000) in 18 countries.
1. Create a scatterplot of the data, with Wine as the explanatory variable. Does there appear to be a transformation of the data needed?
2. Does the data suggest that wine consumption is associated with heart disease?
3. Would this study be evidence that if a person who increases their wine consumption to 75 liters per year, then their odds of dying from heart disease would change?
The data frame datasaurus_dozen is part of the datasauRus package. This data is actually 13 data sets, each one specified by a different value of the dataset variable. For each of the 13 data sets, compute \(\bar{x}\),\(\bar{y}\),\(s_x\),\(s_y\), and the correlation between \(x\) and \(y\). What do you observe? Plot a few of the individual data sets (including dino) and describe what you see.
Theorem 10.1 gives a value for \(\beta_1\) in terms of the data \((x_1,y_1),\ldots,(x_n, y_n)\). Use Theorem 10.1 to compute the value for \(\beta_0\).
Consider the model \(y_i = \beta_0 + x_i + \epsilon_i\). That is, assume that the slope is 1. Find the value of \(\beta_0\) that minimizes the sum-squared error when fitting the line \(y = \beta_0 + x\) to data given by \((x_1,y_1),\ldots,(x_n, y_n)\).
Consider the model \(y_i = \beta_1x_i + \epsilon_i\). That is, assume that the intercept is 0. Find the value of \(\beta_1\) that minimizes the sum-squared error when fitting the line \(y = \beta_1 x\) to data given by \((x_1,y_1),\ldots,(x_n, y_n)\).
Suppose that, instead of minimizing the sums of squares of the vertical error \(\sum (\beta_1 x_i - y_i)^2\), you decide to minimize the sums of squares of the horizontal error. This means that our model is that \(x = \gamma y + \epsilon\) and we wish to minimize \(\sum (x_i - \gamma y_i)^2\) over all choices of \(\gamma\).
1. Find a formula for \(\gamma\).
2. Find an example where the “best” line determined by minimizing vertical error is different from the “best” line determined by minimizing horizontal error.
Suppose you terribly incorrectly model \(y = x^2 + \epsilon\) based on a linear model \(y = \beta_0 + \beta_1x + \epsilon\). Assume you have 30 data points and that the explanatory data comes uniformly from the interval \([0, 10]\). What percentage of time is new data at \(x = 5\) in the 95% prediction interval at \(x = 5\)? At \(x = 10\)?
What changes in the simulation of prediction intervals need to be made if we choose our original \(x\) values to be \(0, 0.5, 1, 1.5, 2, 2.5, \ldots, 9.5, 10\)? Does a 95% prediction interval still contain new data 95% of the time? Think of what your answer should be, and then write code to verify. (Note that in this case, there will be 21 \(x\)-values.)
Simulate 95% confidence intervals for data following \(y_i = 1 + 2x_i + \epsilon_i\), where \(\epsilon_i \sim N(0,1)\). You can assume that the \(x\) values you use are randomly selected between \(0\) and \(10\). Your goal should be to estimate the probability that \(1 + 2x_0\) is in the confidence interval associated with \(x = x_0\). (Hint: modify the code that was given for prediction intervals in the text.)
Create a data set of size 20 that follows the model \(y = 2 + 3x + \epsilon\), where \(\epsilon\sim N(0,1)\). Fit a linear model to the data. Estimate the probability that if you chose a point \(x\) in \([0,10]\) and create a new data point 2 + 3*x + rnorm(1), then that new data point will be in the 95% prediction interval given by your model. Is your answer 95%? Why would you not necessarily expect the answer to be 95%?

Chan AYC, Morgan S-J (2018) Assessing children’s cognitive flexibility with the Shape Trail Test. PLoS ONE 13(5): e0198254. https://doi.org/10.1371/journal.pone.0198254 ↩︎
To find this option with R’s built-in help, use ?predict and then click on predict.lm, because we are applying predict to an object created by lm.↩︎
Viecelli C, Graf D, Aguayo D, Hafen E, Füchslin RM (2020) Using smartphone accelerometer data to obtain scientific mechanical-biological descriptors of resistance exercise training. PLOS ONE 15(7): e0235156. https://doi.org/10.1371/journal.pone.0235156 ↩︎
Blomkvist, Andreas & Andersen, Stig & de Bruin, Eling & Jorgensen, Martin. (2016). Unilateral lower limb strength assessed using the Nintendo Wii Balance Board: a simple and reliable method. Aging Clinical and Experimental Research. 29. 10.1007/s40520-016-0692-5.↩︎
“Do Pulitzers Help Newspapers Keep Readers?”, FiveThirtyEight, April 15, 2014. https://fivethirtyeight.com/features/do-pulitzers-help-newspapers-keep-readers/↩︎
Churcher TS, Sinden RE, Edwards NJ, Poulton ID, Rampling TW, Brock PM, et al. (2017) Probability of Transmission of Malaria from Mosquito to Human Is Regulated by Mosquito Parasite Density in Naïve and Vaccinated Hosts. PLoS Pathog 13(1): e1006108. https://doi.org/10.1371/journal.ppat.1006108.↩︎