Chapter 4 Simulation of Random Variables

In this chapter we discuss simulation related to random variables. We will simulate probabilities related to random variables, and more importantly for our purposes, we will simulate pdfs and pmfs of random variables.

4.1 Estimating probabilities of rvs via simulation.

In order to run simulations with random variables, we will use the R command r + distname, where distname is the name of the distribution, such as unif, geom, pois, norm, exp or binom. The first argument to any of these functions is the number of samples to create.

Most distname choices can take additional arguments that affect their behavior. For example, if I want to create a random sample of size 100 from a normal random variable with mean 5 and sd 2, I would use rnorm(100, mean = 5, sd = 2), or simply rnorm(100, 5, 2). Without the additional arguments, rnorm gives the standard normal random variable, with mean 0 and sd 1. For example, rnorm(10000) gives 10000 random values of the standard normal random variable \(Z\).

Our strategy for estimating probabilities using simulation is as follows. We first create a large (approximately 10,000) sample from the distribution(s) in question. Then, we use the mean function to compute the percentage of times that the event we are interested in occurs. If the sample size is reasonably large and representative, then the true probability that the event occurs should be close to the percentage of times that the event occurs in our sample. It can be useful to repeat this procedure a few times to see what kind of variation we obtain in our answers.

Example Let \(Z\) be a standard normal random variable. Estimate \(P(Z > 1)\).

We begin by creating a large random sample from a normal random variable.

simdata <- rnorm(10000)

Next, we compute the percentage of times that the sample is greater than one. First, we create a vector that contains TRUE at each index of the sample that is greater than one, and contains FALSE at each index of the sample that is less than or equal to one.

log_vec <- simdata > 1
head(log_vec)

## [1] FALSE FALSE FALSE FALSE  TRUE  TRUE

Now, we count the number of times we see a TRUE, and divide by the length of the vector.

sum(log_vec == TRUE)/10000

## [1] 0.1579

There are a few improvements we can make. First, log_vec == TRUE is just the same as log_vec, so we can compute

sum(log_vec)/10000

## [1] 0.1579

Lastly, we note that sum converts TRUE to 1 and FALSE to zero. We are adding up these values and dividing by the length, which is the same thing as taking the mean. So, we can just do

mean(log_vec)

## [1] 0.1579

For simple problems, it is often easier to omit the intermediate step(s) and write

mean(simdata > 1)

## [1] 0.1579

Example Let \(Z\) be a standard normal rv. Estimate \(P(Z^2 > 1)\).

simdata <- rnorm(10000)
mean(simdata^2 < 1)

## [1] 0.6821

We can also easily estimate means and standard deviations of random variables. To do so, we create a large random sample from the distribution in question, and we take the sample mean or sample standard deviation of the large sample. If the sample is large and representative, then we expect the sample mean to be close to the true mean, and the sample standard deviation to be close to the true standard deviation. Let’s begin with an example where we know what the correct answer is, in order to check that the technique is working.

Example Let \(Z\) be a normal random variable with mean 0 and standard deviation 1. Estimate the mean and standard deviation of \(Z\).

simdata <- rnorm(10000, 0, 1)
mean(simdata)

## [1] -0.004031672

sd(simdata)

## [1] 0.993022

We see that we are reasonably close to the correct answers of 0 and 1.

Example Estimate the mean and standard deviation of \(Z^2\).

simdata <- rnorm(10000)
mean(simdata^2)

## [1] 1.012903

sd(simdata^2)

## [1] 1.425278

We will see later in this chapter that \(Z^2\) is a \(\chi^2\) random variable with one degree of freedom, and it is known that a \(\chi^2\) random variable with \(\nu\) degrees of freedom has mean \(\mu\) and standard deviation \(\sqrt{2\nu}\). Thus, the answers above are pretty close to the correct answers.

Example Let \(X\) and \(Y\) be independent standard normal random variables. Estimate \(P(XY > 1)\).

There are two ways to do this. The first is:

x <- rnorm(10000)
y <- rnorm(10000)
mean(x*y > 1)

## [1] 0.1046

A technique that is closer to what we will be doing below is the following. We want to create a random sample from the random variable \(Z = XY\). To do so, we would use

simdata <- rnorm(10000) * rnorm(10000)

Note that R multiples the vectors componentwise. Then, we compute the percentage of times that the sample is greater than 1 as before.

mean(simdata > 1)

## [1] 0.1006

Note that (1) this is not the same as the answer we got for \(P(Z^2 > 1)\), and (2) we get different, but similar, answers when we run the simulation twice.

4.2 Estimating discrete distributions

In this section, we show how to estimate via simulation the pmf of a discrete random variable. Let’s begin with an example.

Example Suppose that two dice are rolled, and their sum is denoted as \(X\). Estimate the pmf of \(X\) via simulation.

Recall that if we wanted to estimate the probability that \(X = 2\), for example, we would use

simdata <- replicate(10000, {
  dieRoll <- sample(1:6, 2, TRUE)
  sum(dieRoll)
})
mean(simdata == 2)

## [1] 0.0306

It is possible to repeat this replication for each value \(2,\ldots, 12\), but that would take a long time. More efficient is to keep track of all of the observations of the random variable, and divide each by the number of times the rv was observed. We will use table for this. Recall, table gives a vector of counts of each unique element in a vector. That is,

table(c(1,1,1,1,1,2,2,3,5,1))

## 
## 1 2 3 5 
## 6 2 1 1

indicates that there are 6 occurrences of “1”, 2 occurrences of “2”, and 1 occurrence each of “3” and “5”. To apply this to the die rolling, we create a vector of length 10,000 that has all of the observances of the rv \(X\), in the following way:

set.seed(1)
simdata <- replicate(10000, {
  dieRoll <- sample(1:6, 2, TRUE)
  sum(dieRoll)
})
table(simdata)

## simdata
##    2    3    4    5    6    7    8    9   10   11   12 
##  300  547  822 1080 1412 1655 1418 1082  846  562  276

We then divide each by 10,000 to get the estimate of the pmf:

set.seed(1)
simdata <- replicate(10000, {
  dieRoll <- sample(1:6, 2, TRUE)
  sum(dieRoll)
})
table(simdata)/10000

## simdata
##      2      3      4      5      6      7      8      9     10     11     12 
## 0.0300 0.0547 0.0822 0.1080 0.1412 0.1655 0.1418 0.1082 0.0846 0.0562 0.0276

And, there is our estimate of the pmf of \(X\). For example, we estimate the probability of rolling an 11 to be 0.0581.

Example Suppose fifty randomly chosen people are in a room. Let \(X\) denote the number of people in the room who have the same birthday as someone else in the room. Estimate the pmf of \(X\).

We will simulate birthdays by taking a random sample from 1:365 and storing it in a vector. The tricky part is counting the number of elements in the vector that are repeated somewhere else in the vector. We will create a table and add up all of the values that are bigger than 1. Like this:

birthdays <- sample(1:365, 50, replace = TRUE)
table(birthdays)

## birthdays
##   8   9  13  20  24  41  52  64  66  70  92  98  99 102 104 119 123 126 151 175 
##   2   1   1   2   2   1   1   1   1   1   1   1   1   1   1   1   1   1   1   1 
## 179 182 185 222 231 237 240 241 249 258 259 276 279 285 287 313 317 323 324 327 
##   1   1   1   1   1   1   1   1   1   1   2   2   1   1   1   1   1   1   1   1 
## 333 344 346 364 365 
##   1   1   1   1   1

We look through the table and see that anywhere there is a number bigger than 1, there are that many people who share that birthday. To count the number of people who share a birthday with someone else:

sum(table(birthdays)[table(birthdays) > 1])

## [1] 10

Now, we put that inside replicate, just like in the previous example.

set.seed(1)
simdata <- replicate(10000, {
  birthdays <- sample(1:365, 50, replace = TRUE)
  sum(table(birthdays)[table(birthdays) > 1])
})
table(simdata)/10000

## simdata
##      0      2      3      4      5      6      7      8      9     10     11 
## 0.0309 0.1196 0.0059 0.1982 0.0219 0.2146 0.0309 0.1688 0.0293 0.0917 0.0205 
##     12     13     14     15     16     17     18     19     21 
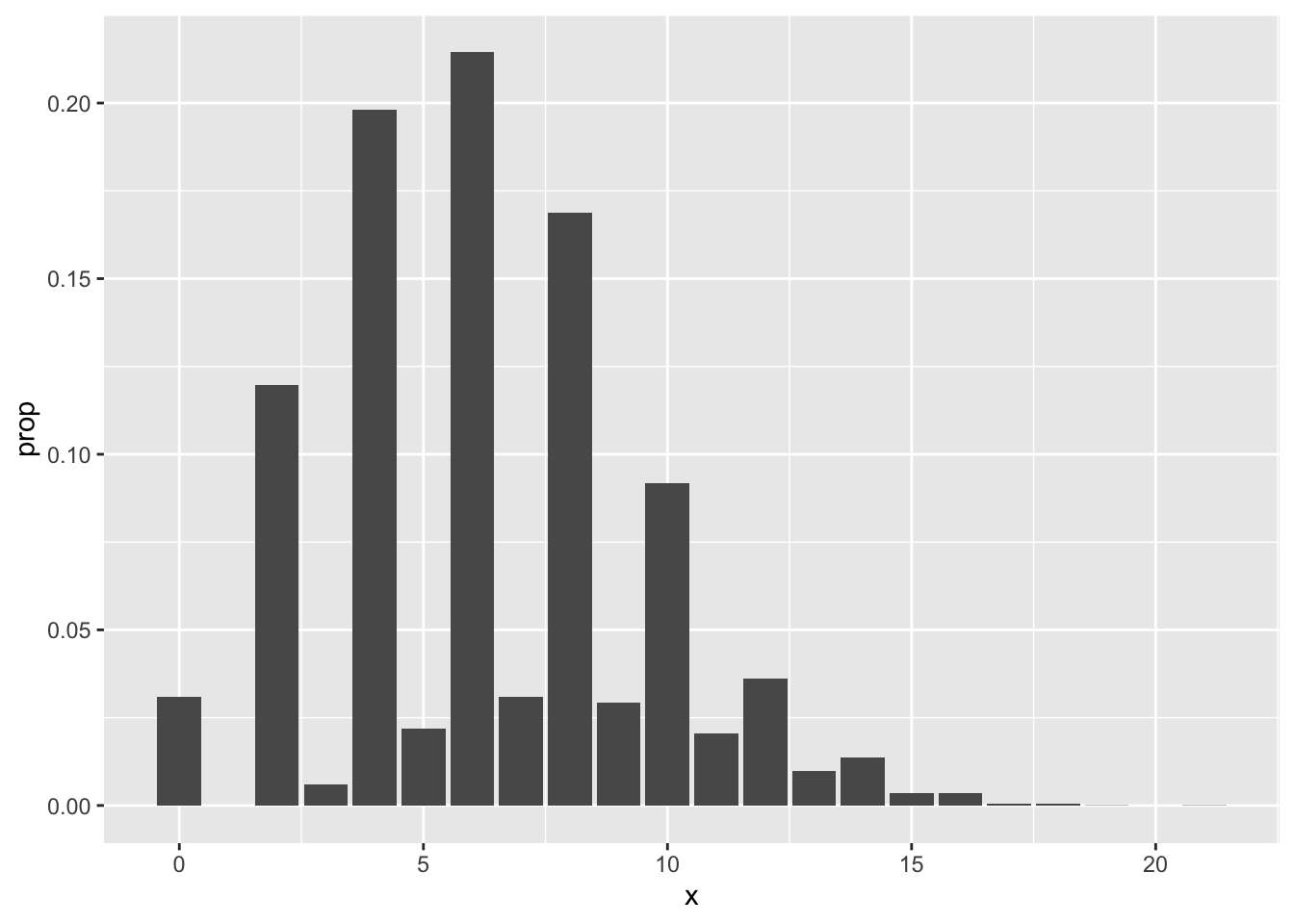
## 0.0361 0.0097 0.0137 0.0034 0.0034 0.0006 0.0006 0.0001 0.0001

Looking at the pmf, our best estimate is that the most likely outcome is that 6 people in the room share a birthday with someone else, followed closely by 4 and then 8. Note that it is impossible for exactly one person to share a birthday with someone else in the room! It would be preferable for several reasons to have the observation \(P(X = 1) = 0\) listed in the table above, but we leave that for another day. Plotting the pmf from the table output is a little more complicated than we need to get into right now, but here is a plot.¹⁰

Example You flip a coin 100 times. After each flip, either there have been more heads, more tails, or the same number of heads and tails. Let \(X\) be the number of times in the 100 flips that there were more heads than tails. Estimate the pmf of \(X\). Before looking at the solution below, try to guess whether the pmf of \(X\) will be centered around 50, or not.

We start by doing a single run of the experiment. Recall that the function cumsum accepts a numeric vector and returns the cumulative sum of the vector. So, cumsum(c(1, 3, -1)) would return c(1, 4, 3).

coin_flips <- sample(c("H", "T"), 100, replace = TRUE) #flip 100 coins
num_heads <- cumsum(coin_flips == "H") #cumulative number of heads so far
num_tails <- cumsum(coin_flips == "T") #cumulative number of tails so far
sum(num_heads > num_tails) #number of times there were more heads than tails

## [1] 0

Now, we put that inside of replicate.

simdata <- replicate(100000, {
  coin_flips <- sample(c("H", "T"), 100, replace = TRUE)
  num_heads <- cumsum(coin_flips == "H")
  num_tails <- cumsum(coin_flips == "T")
  sum(num_heads > num_tails) 
})

When we have this many possible outcomes, it is easier to view a plot of the pmf than to look directly at the table of probabilities.

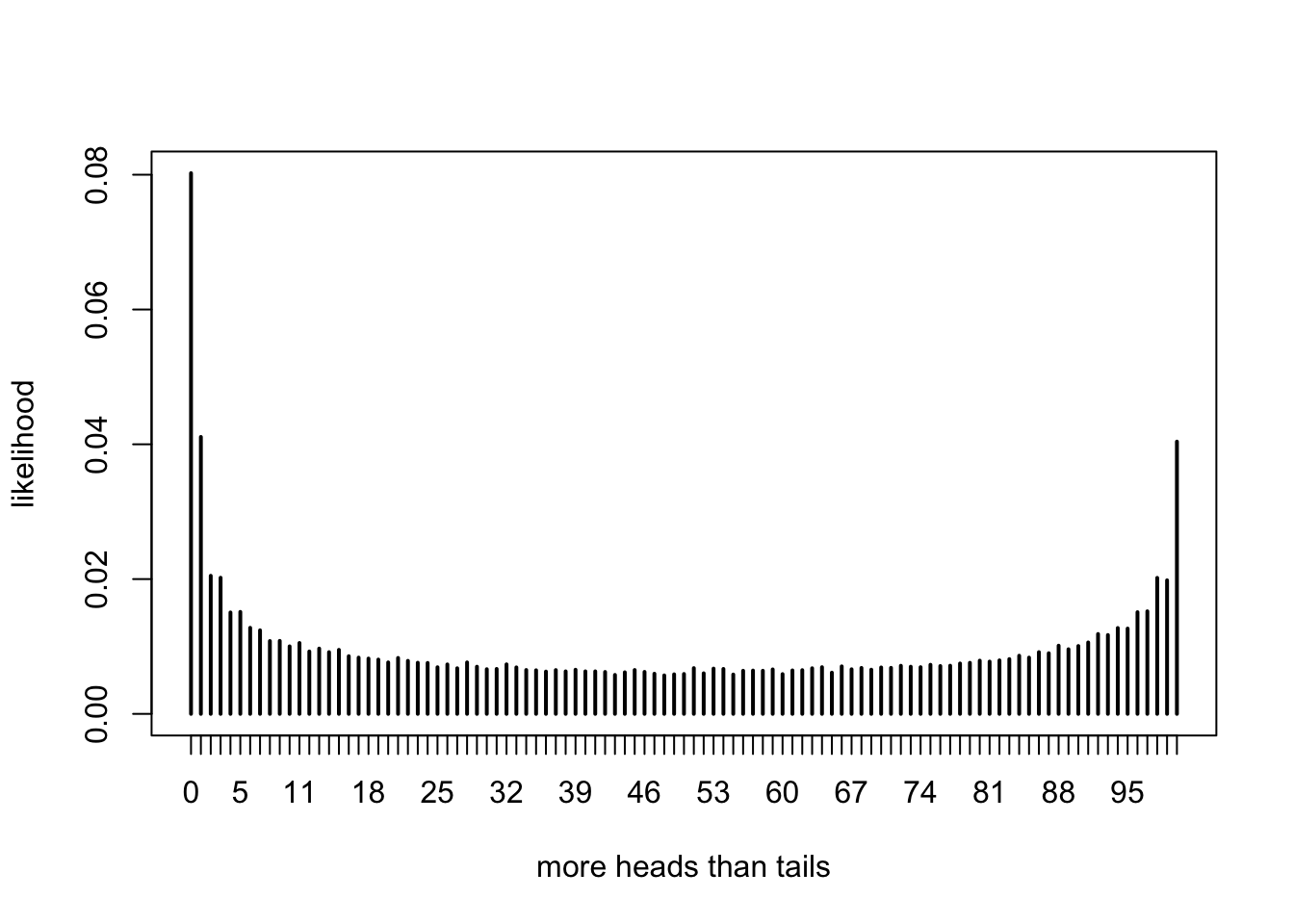
plot(table(simdata)/100000, ylab = "likelihood", xlab = "more heads than tails")

We see that the most likely outcome (by far) is that there are never more heads than tails in the 100 tosses of the coin. This result can be surprising, even to experienced mathematicians.

Example Suppose you have a bag full of marbles; 50 are red and 50 are blue. You are standing on a number line, and you draw a marble out of the bag. If you get red, you go left one unit. If you get blue, you go right one unit. You draw marbles up to 100 times, each time moving left or right one unit. Let \(X\) be the number of marbles drawn from the bag until you return to 0 for the first time. Estimate the pmf of \(X\).

movements <- sample(rep(c(1, -1), times = 50), 100, FALSE)
movements[1:10]

##  [1] -1  1  1 -1  1 -1  1 -1  1  1

cumsum(movements)[1:10]

##  [1] -1  0  1  0  1  0  1  0  1  2

which(cumsum(movements) == 0)

##  [1]   2   4   6   8  22  28  30  32  34  36  86  94  96  98 100

min(which(cumsum(movements) == 0))

## [1] 2

Now, we just need to table it like we did before.

table(replicate(10000, {
  movements <- sample(rep(c(1, -1), times = 50), 100, FALSE)
  min(which(cumsum(movements) == 0)) 
}))/10000

## 
##      2      4      6      8     10     12     14     16     18     20     22 
## 0.5095 0.1285 0.0640 0.0391 0.0280 0.0193 0.0180 0.0151 0.0129 0.0105 0.0080 
##     24     26     28     30     32     34     36     38     40     42     44 
## 0.0084 0.0076 0.0068 0.0056 0.0043 0.0068 0.0043 0.0048 0.0043 0.0036 0.0040 
##     46     48     50     52     54     56     58     60     62     64     66 
## 0.0031 0.0047 0.0021 0.0037 0.0031 0.0025 0.0025 0.0027 0.0026 0.0029 0.0027 
##     68     70     72     74     76     78     80     82     84     86     88 
## 0.0025 0.0025 0.0017 0.0019 0.0023 0.0027 0.0025 0.0029 0.0026 0.0027 0.0026 
##     90     92     94     96     98    100 
## 0.0029 0.0029 0.0041 0.0028 0.0054 0.0090

4.3 Estimating continuous distributions

In this section, we show how to estimate the pdf of a continuous rv via simulation. As opposed to the discrete case, we will not get an explicit formula for the pdf, but we will rather get a graph of it.

Example Estimate the pdf of \(2Z\) when \(Z\) is a standard normal random variable

Our strategy is to take a random sample of size 10,000 and use either the R function geom_density inside of ggplot2 or the hist function to estimate the pdf. As before, we build our sample of size 10,000 up as follows:

A single value sampled from standard normal rv:

z <- rnorm(1)

We multiply it by 2 to get a single value sampled from \(2Z\).

2 * z

## [1] 0.03234922

Now create 10,000 values of \(2Z\):

zData <- 2 * rnorm(10000)

We then use density to estimate and plot the pdf of the data:

plot(density(zData))

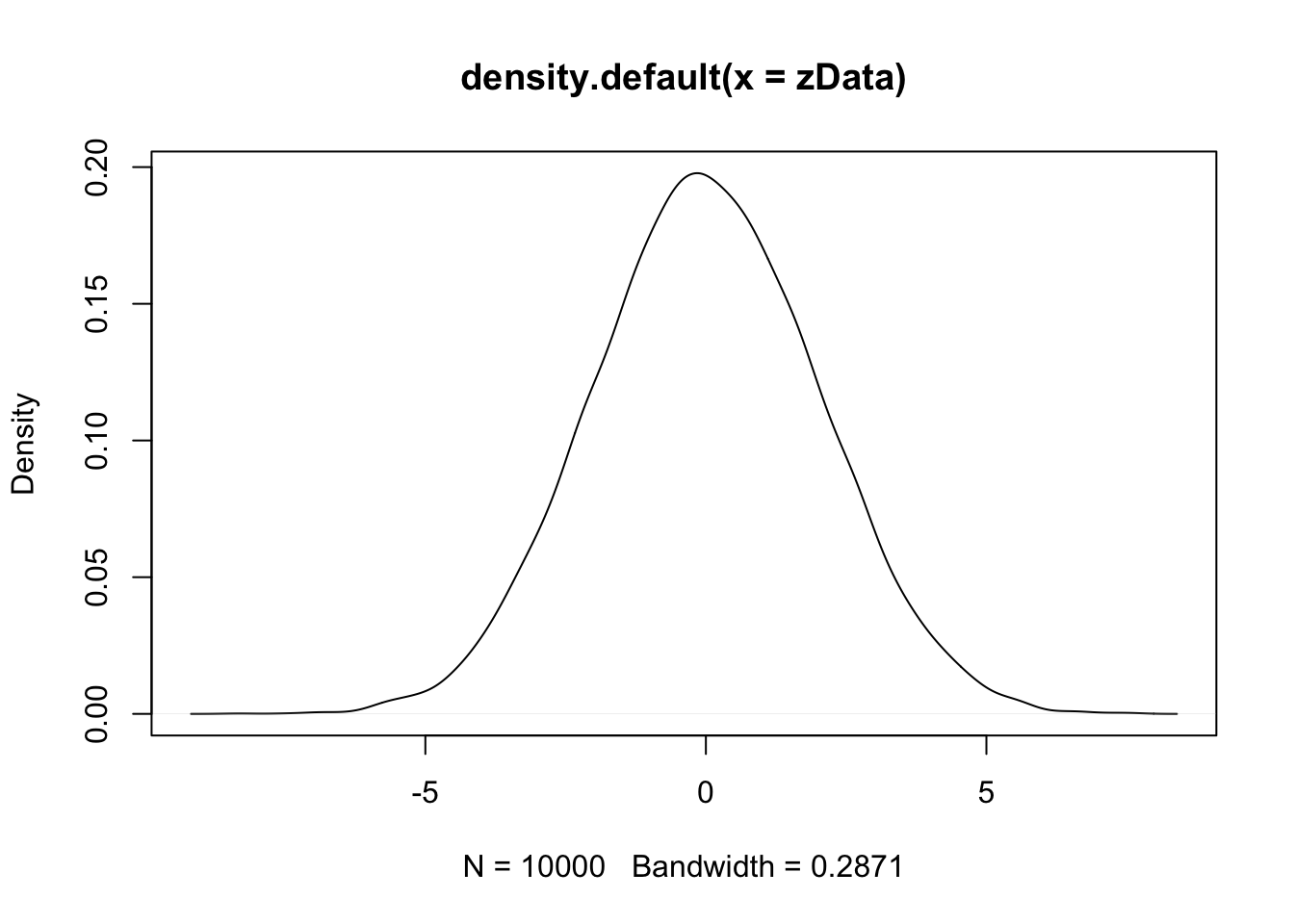
Notice that the most likely outcome of \(2Z\) seems to be centered around 0, just as it is for \(Z\), but that the spread of the distribution of \(2Z\) is twice as wide as the spread of \(Z\).

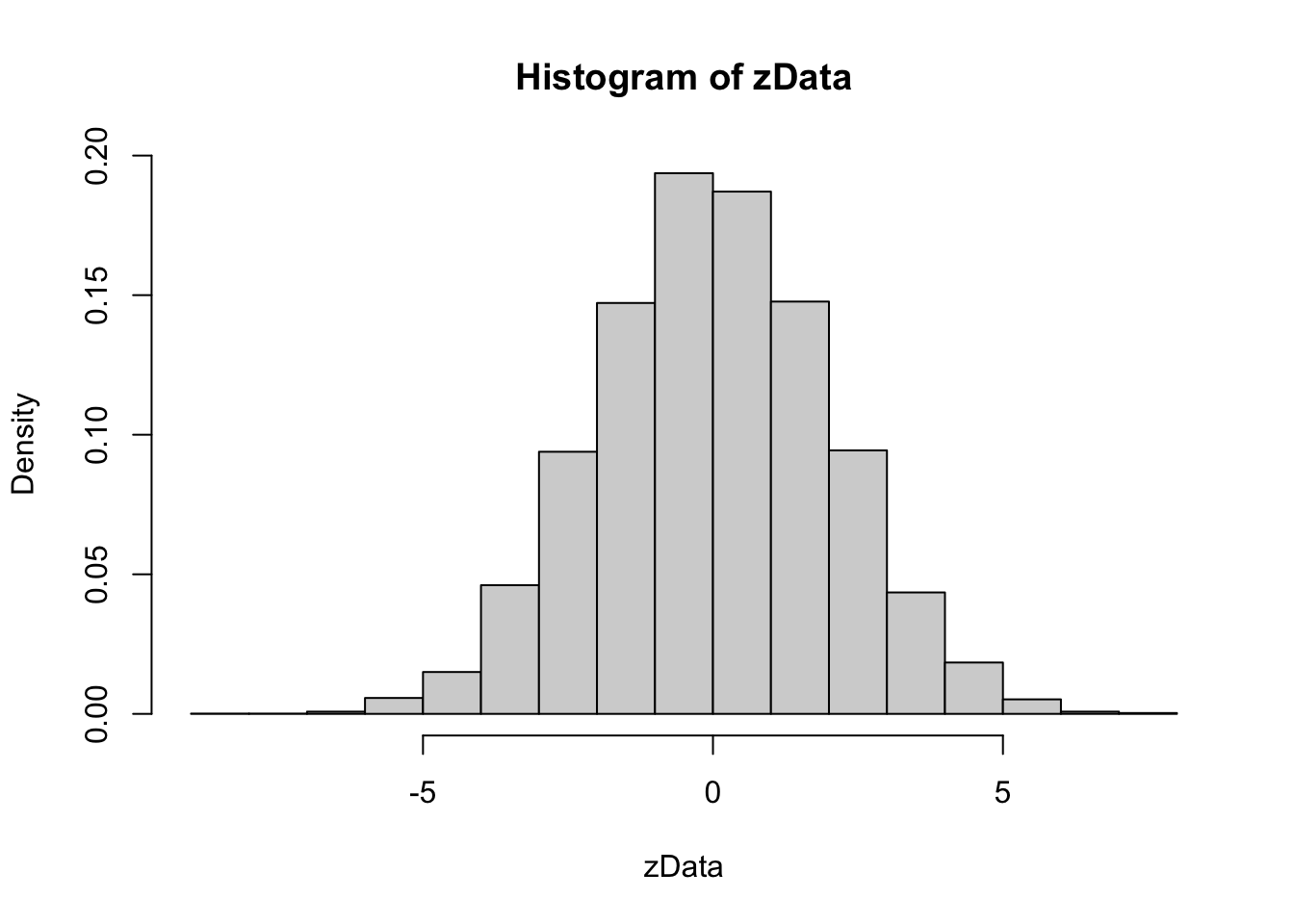
Alternatively, we could have created a histogram of the data, using hist. We set probability = TRUE to adjust the scale on the y-axis so that the area of each rectangle in the histogram is the probability that the random variable falls in the interval given by the base of the rectangle. This will be useful later when we plot pdfs on top of the histogram.

hist(zData, probability = TRUE)

Example Estimate via simulation the pdf of \(\log\bigl(\left|Z\right|\bigr)\) when \(Z\) is standard normal.

expData <- log(abs(rnorm(10000)))
plot(density(expData))

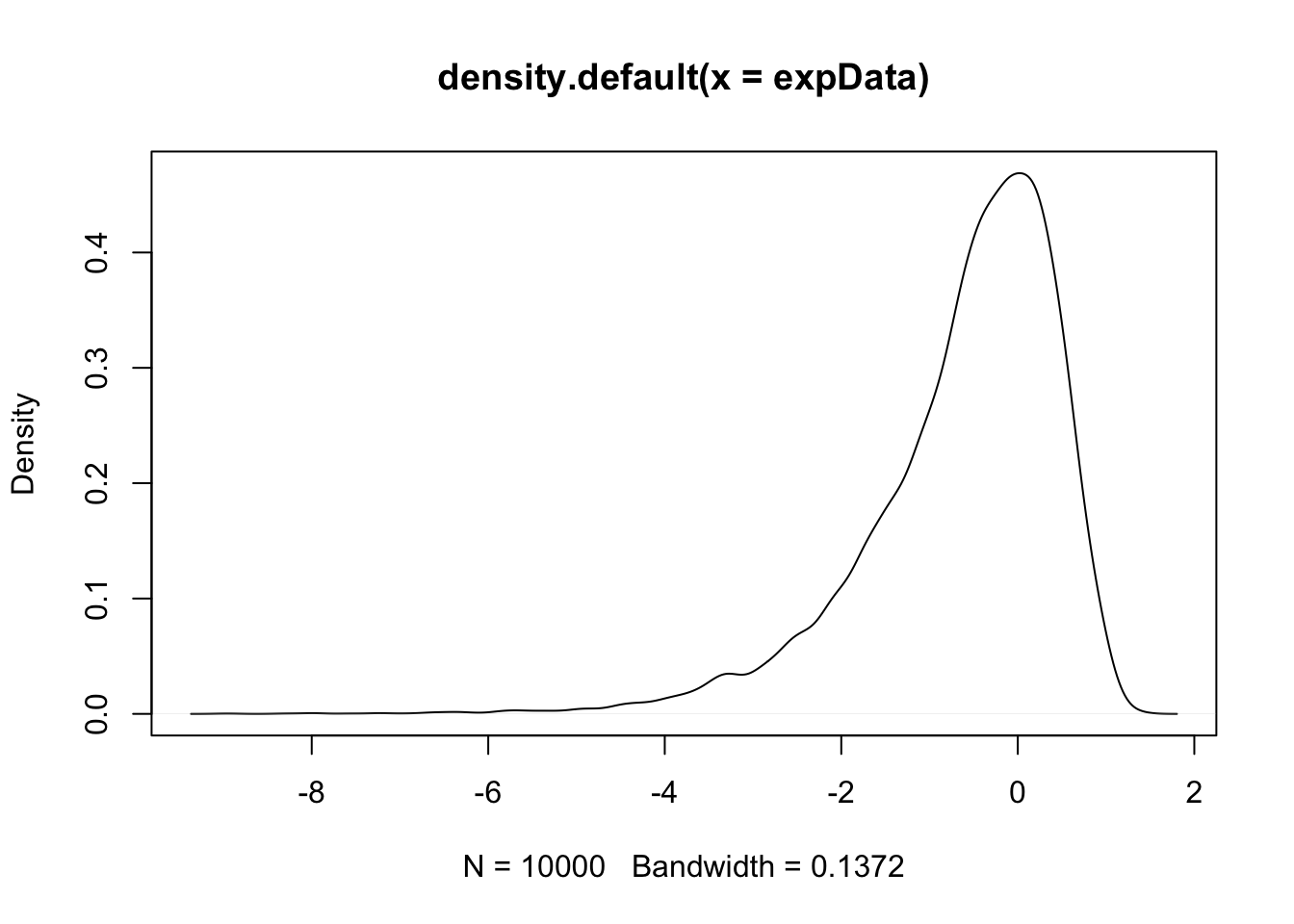
Both of the above worked pretty well, but there are issues when your pdf has discontinuities. Let’s see.

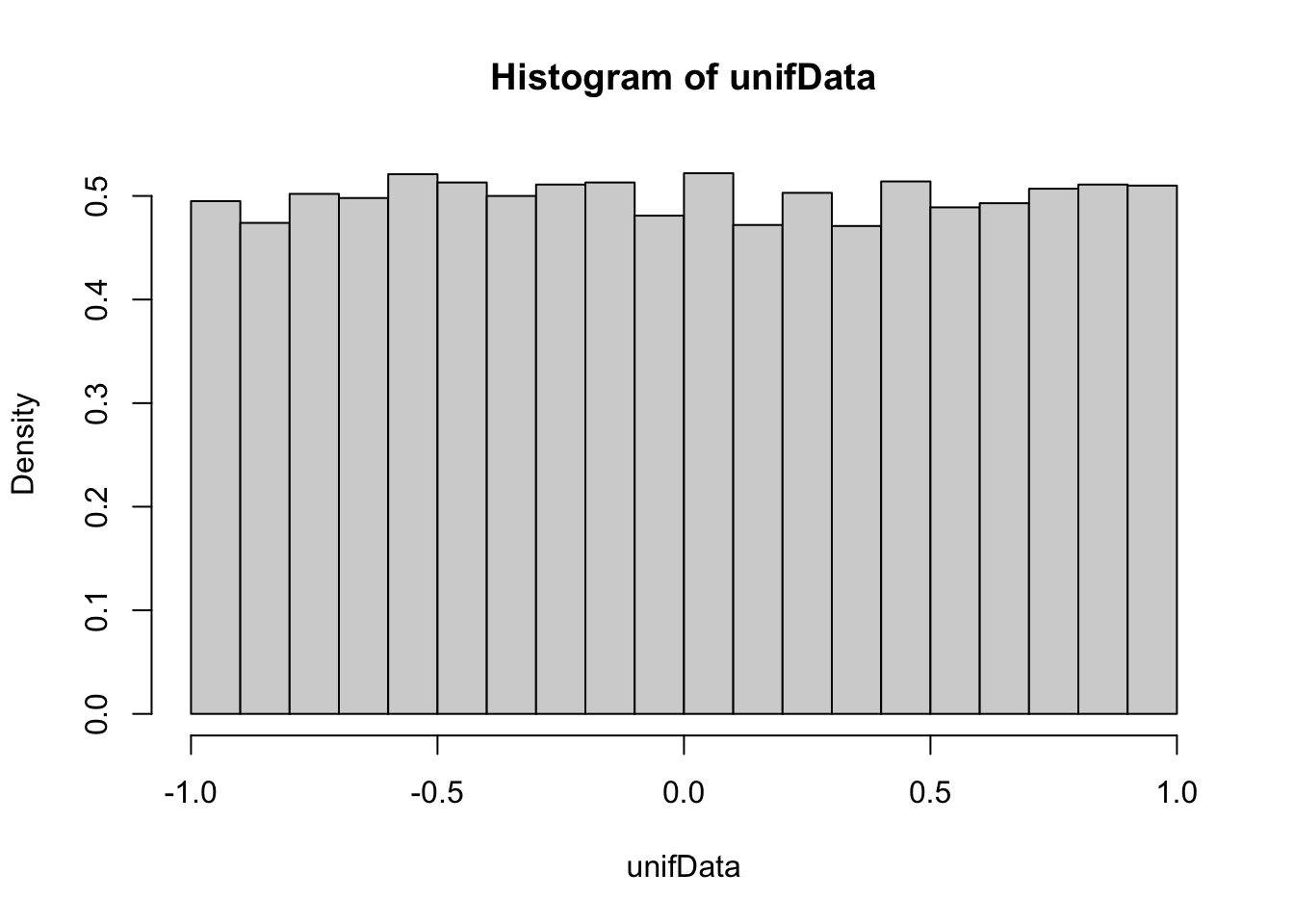
Example Estimate the pdf of \(X\) when \(X\) is uniform on the interval \([-1,1]\).

unifData <- runif(10000,-1,1)
plot(density(unifData))

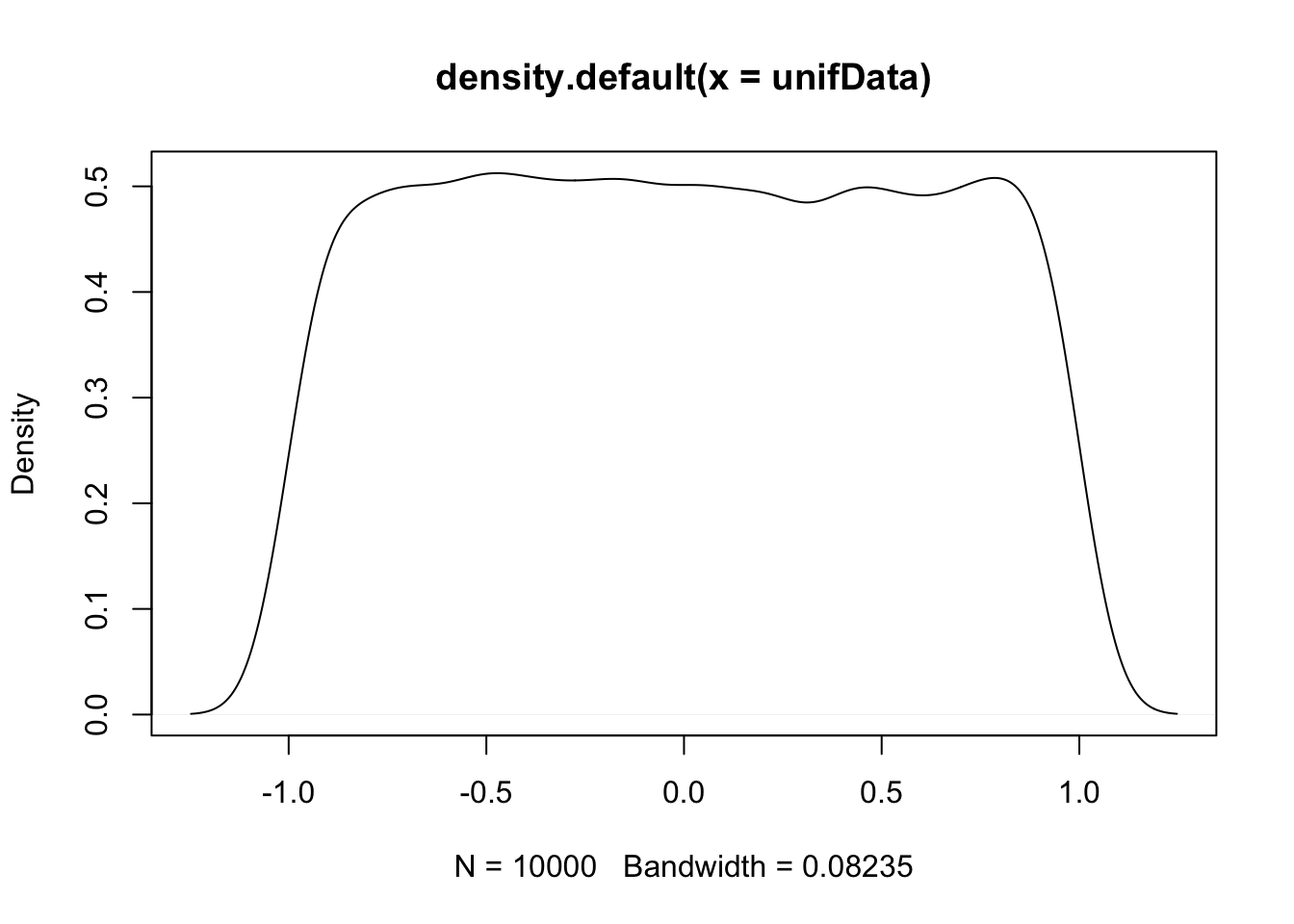
This distribution should be exactly 0.5 between -1 and 1, and zero everywhere else. The simulation is reasonable in the middle, but the discontinuities at the endpoints are not shown well. Increasing the number of data points helps, but does not fix the problem. Compare with the histogram approach, which seems to work better when the data comes from a distribution with a jump discontinuity.

hist(unifData, probability = TRUE)

Example Estimate the pdf of \(X^2\) when \(X\) is uniform on the interval \([-1,1]\).

simdata <- replicate(10000, {
  unif_sample <- runif(1, -1, 1)
  unif_sample^2
})
plot(density(simdata))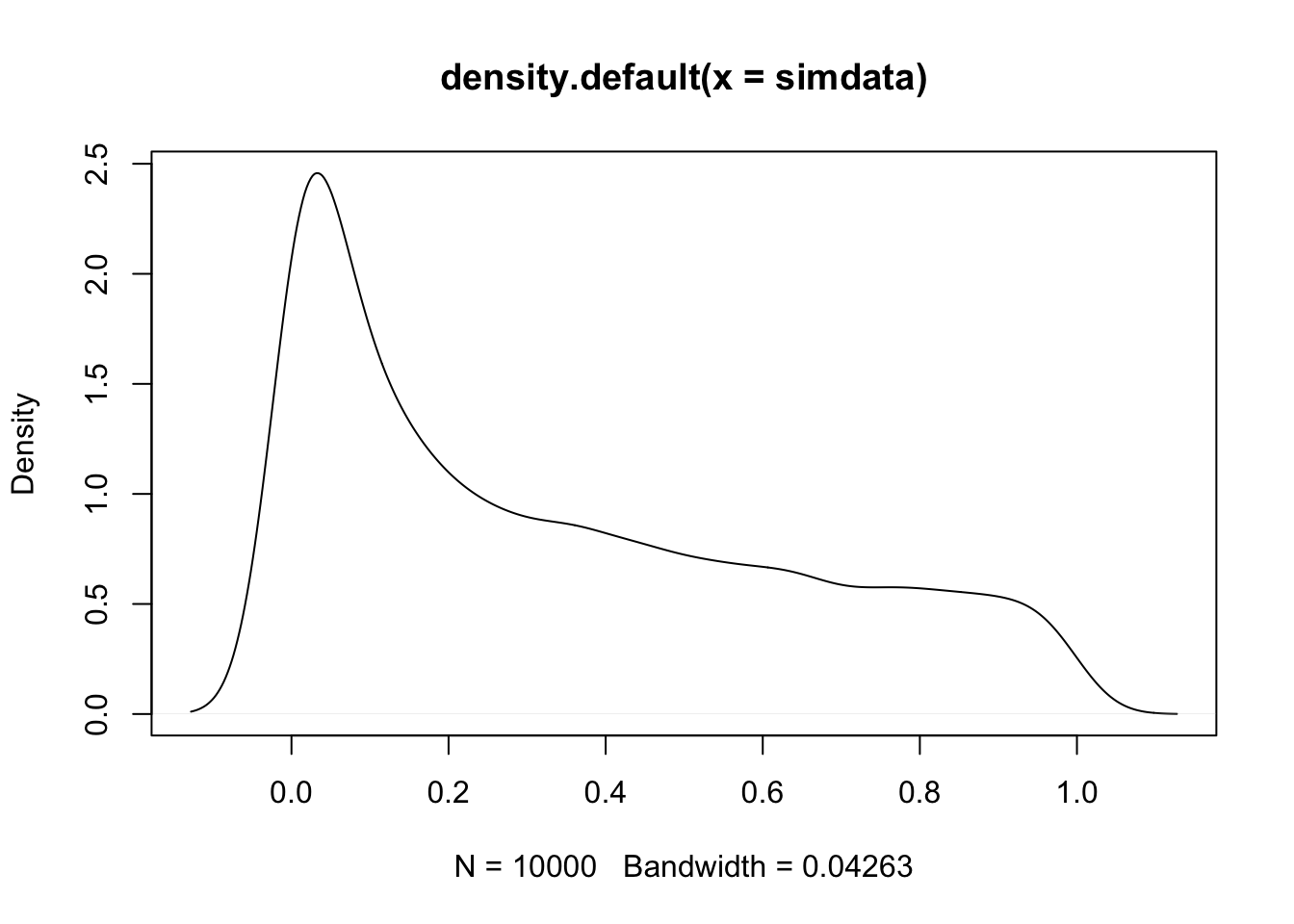

Example Estimate the pdf of \(X + Y\) when \(X\) and \(Y\) are exponential random variables with rate 2.

simdata <- replicate(10000, {
  x <- rexp(1, 2)
  y <- rexp(1, 2)
  x + y
})
hist(simdata, probability = TRUE)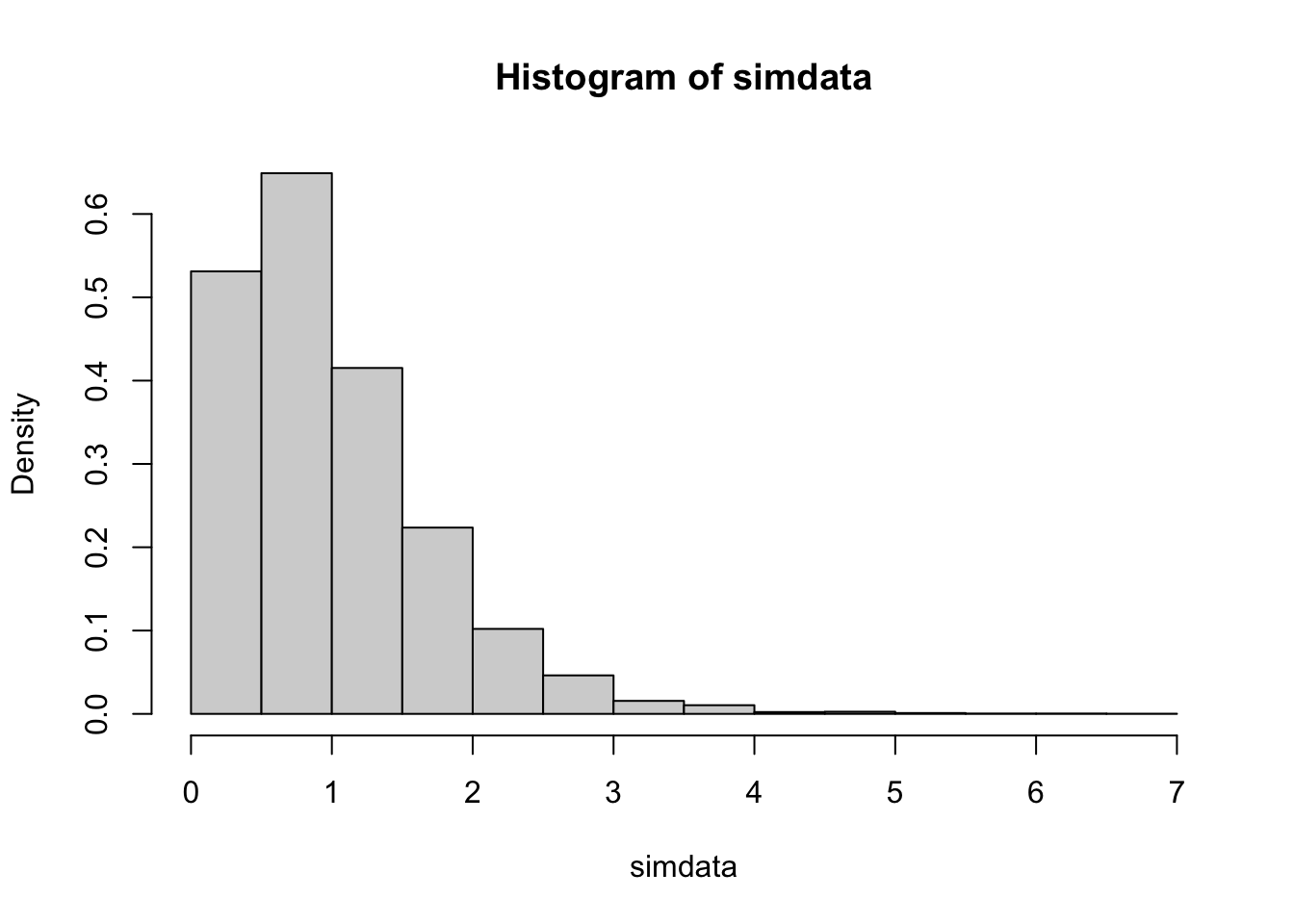

Example Estimate the density of \(X_1 + X_2 + \cdots + X_{20}\) when all of the \(X_i\) are exponential random variables with rate 2.

This one is trickier and the first one for which it is significantly easier to use replicate to create the data. Let’s build up the experiment that we are replicating from the ground up.

Here’s the experiment of summing 20 exponential rvs with rate 2:

sum(rexp(20,2))

## [1] 3.436337

Now, we replicate it (10 times to test):

replicate(10, sum(rexp(20,2)))

##  [1] 12.214462 10.755431 13.170513  4.983875 10.259718  7.937500 11.313176
##  [8] 10.192818  7.386954 10.748529

Of course, we don’t want to just replicate it 10 times, we need about 10,000 data points to get a good density estimate.

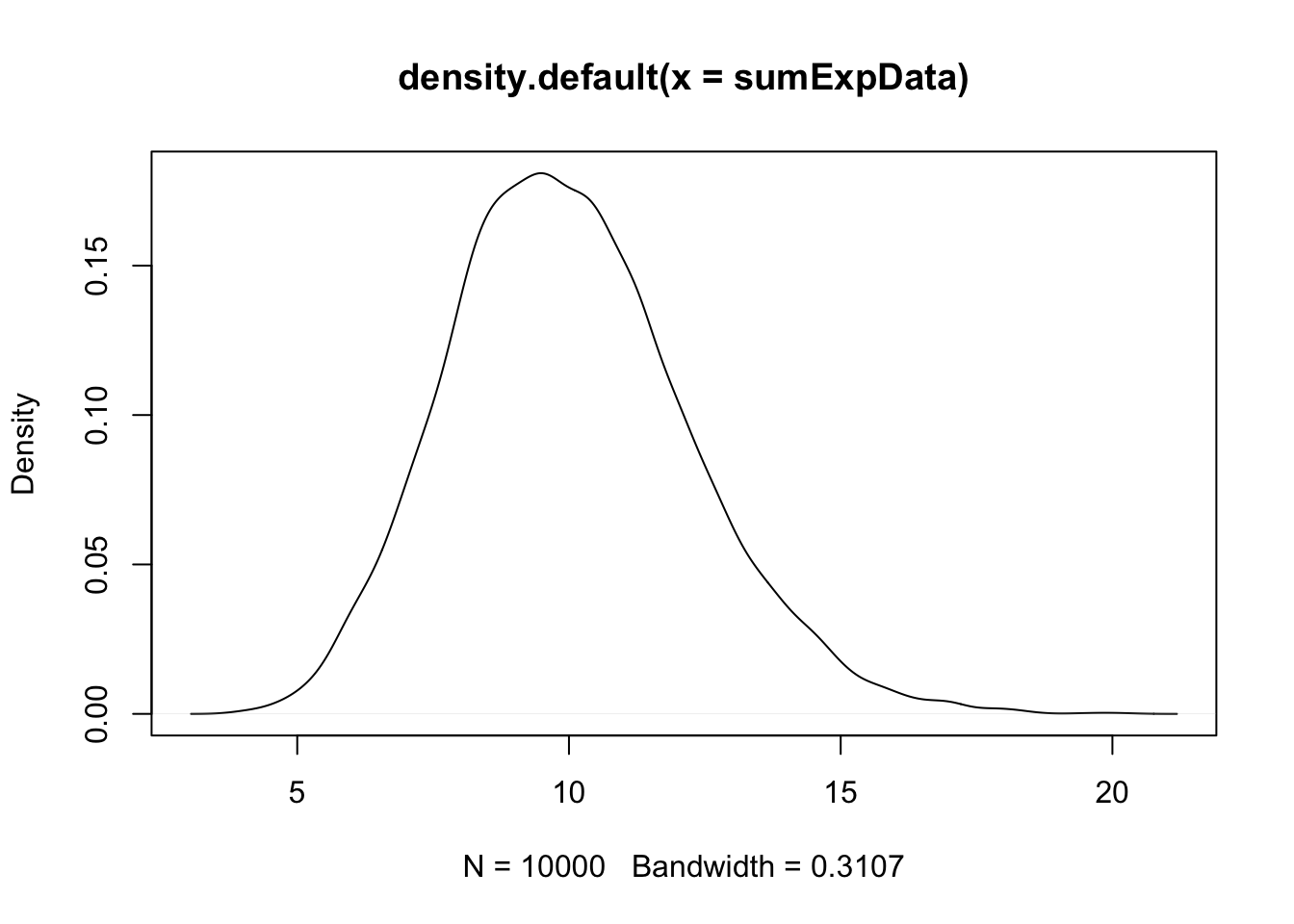
sumExpData <- replicate(10000, sum(rexp(20,2)))
plot(density(sumExpData))

Note that this is starting to look like a normal random variable!!

4.4 Theorems about transformations of random variables

In this section, we will be estimating the pdf of transformations of random variables and comparing them to known pdfs. The goal will be to find a known pdf that closely matches our estimate, so that we can develop some theorems.

Example Compare the pdf of \(2Z\), where \(Z\sim \text{Normal}(0,1)\) to the pdf of a normal random variable with mean 0 and standard deviation 2.

We already saw how to estimate the pdf of \(2Z\), we just need to plot the pdf of \(\text{Normal}(0,2)\) on the same graph. We show how to do this using both the histogram and the density plot approach. The pdf \(f(x)\) of \(\text{Normal}(0,2)\) is given in R by the function \(f(x) = \text{dnorm}(x,0,2)\).

zData <- 2 * rnorm(10000)
hist(zData, probability = TRUE)
curve(dnorm(x, 0, 2), add = T)

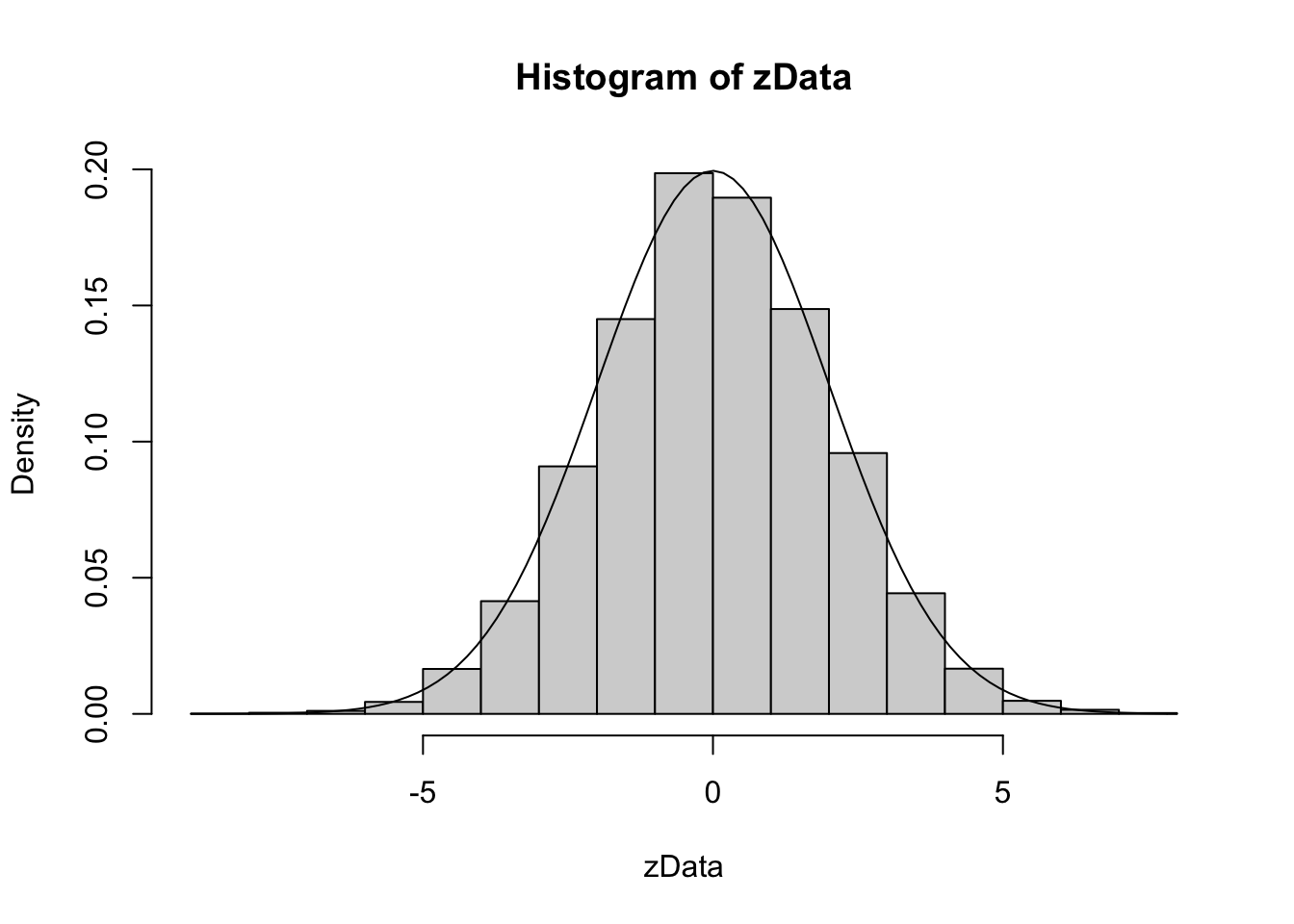
Since the area under of each rectangle in the histogram is approximately the same as the area under the curve over the same interval, this is evidence that \(2Z\) is normal with mean 0 and standard deviation 2. Next, let’s look at the density estimation together with the true pdf of a normal with mean 0 and \(\sigma = 2\).

plot(density(zData), 
     xlab = "zData", 
     main = "Density plot")
curve(dnorm(x, 0, 2), add = T, col = 2)

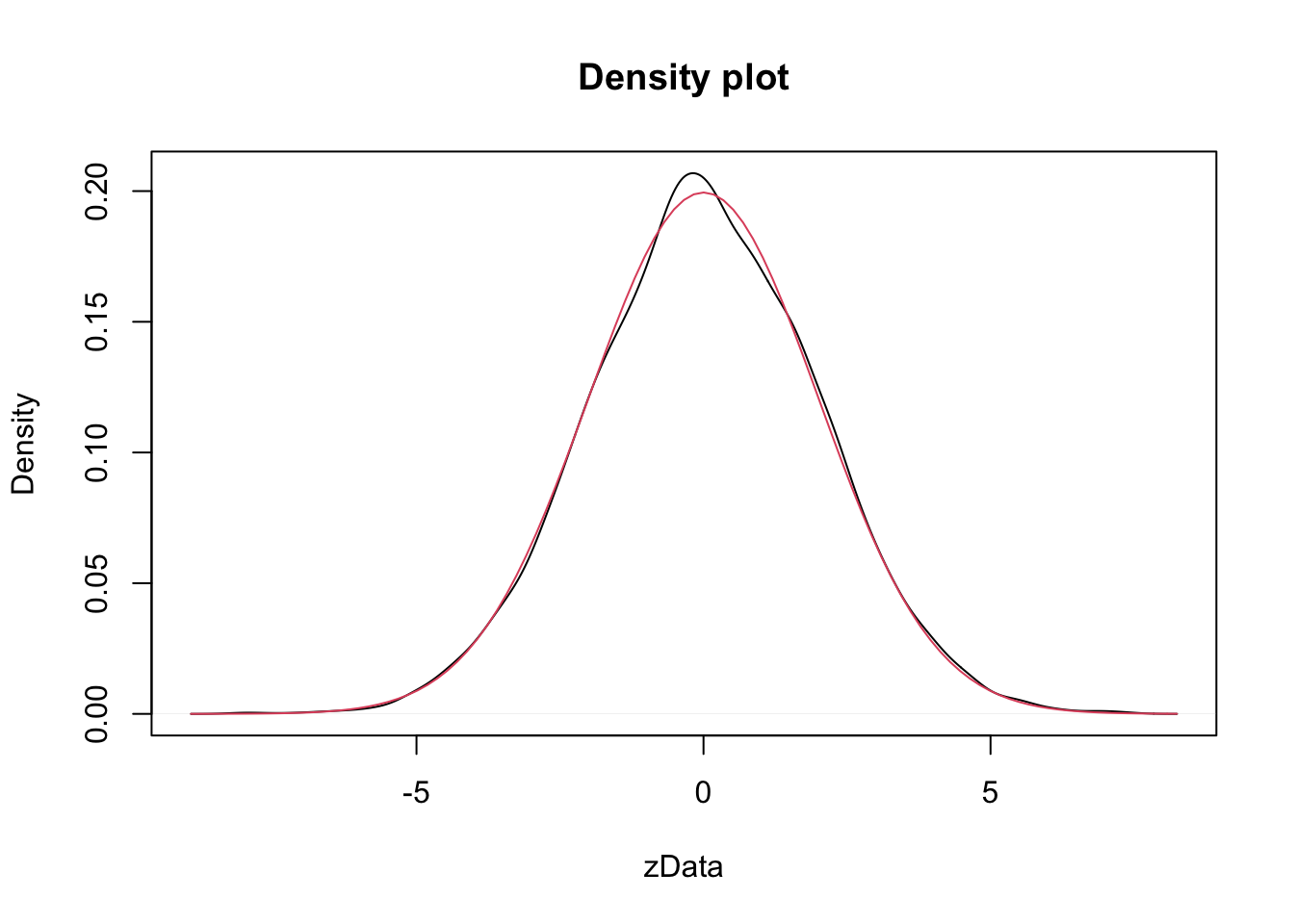
Wow! Those look really close to the same thing! This is again evidence that \(2Z \sim N(0, 2)\). If you want to create a prettier plot with labels, we recommend using ggplot2, which will be discussed in Chapter 6.

Theorem 4.1 Let \(X\) be a normal random variable with mean \(\mu\) and standard deviation \(\sigma\). Then, \(aX + b\) is a normal random variable with mean \(a\mu + b\) and standard deviation \(a\sigma\).

Example Let \(Z\) be a standard normal rv. Find the pdf of \(Z^2\) and compare it to the pdf of a \(\chi^2\) (chi-squared) rv with one degree of freedom. The distname for a \(\chi^2\) rv is chisq, and rchisq requires the degrees of freedom to be specified using the df parameter.

We plot the pdf of \(Z^2\) and the chi-squared rv with one degree of freedom on the same plot. \(\chi^2\) with one df has a vertical asymptote at \(x = 0\), so we need to explicitly set the \(y\)-axis scale:

zData <- rnorm(10000)^2
hist(zData, probability = T)
curve(dchisq(x, df = 1), add = T)

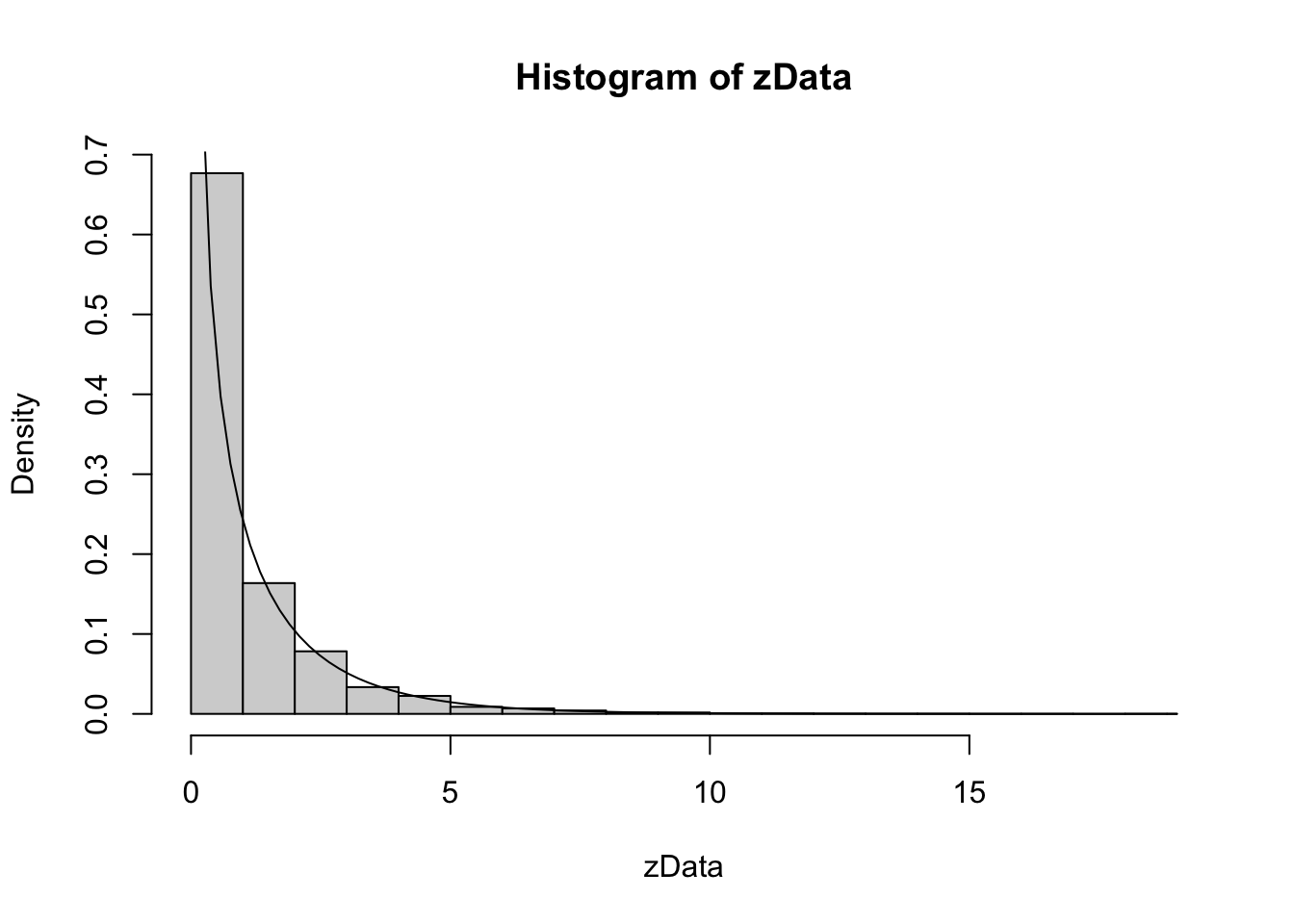
As you can see, the estimated density follows the true histogram quite well. This is evidence that \(Z^2\) is, in fact, chi-squared.

Theorem 4.2 Let \(Z\) be a normal random variable with mean 0 and standard deviation 1. Then, \(Z^2\) is a chi-squared random variable with 1 degree of freedom.

4.5 The Central Limit Theorem

Theorem 4.3 Central Limit Theorem. Let \(X_1,\ldots,X_n\) be iid rvs with mean \(\mu\) and standard deviation \(\sigma\). Then \[ \frac{\overline{X} - \mu}{\sigma/\sqrt{n}} \to Z \qquad \text{as}\ n \to \infty \] where \(Z\) is a standard normal rv.

We will not prove this theorem, but we will do simulations for several examples. They will all follow a similar format.

Example Let \(X_1,\ldots,X_{30}\) be Poisson random variables with rate 2. From our knowledge of the Poisson distribution, each \(X_i\) has mean \(\mu = 2\) and standard deviation \(\sigma = \sqrt{2}\). The central limit theorem says that \[ \frac{\overline{X} - 2}{\sqrt{2}/\sqrt{30}} \] will be approximately normal with mean 0 and standard deviation 1 if \(n = 30\) is a large enough sample size. We will investigate later how to determine what a large enough sample size would be, but for now we assume that for this case, \(n = 30\) is big enough. Let us check this with a simulation.

This is a little but more complicated than our previous examples, but the idea is still the same. We create an experiment which computes \(\overline{X}\) and then transforms by subtracting 2 and dividing by \(\sqrt{2}/\sqrt{30}\).

Here is a single experiment:

xbar <- mean(rpois(30,2))
(xbar - 2)/(sqrt(2)/sqrt(30))

## [1] 0.9036961

Now, we replicate and plot:

poisData <- replicate(10000, {
  xbar <- mean(rpois(30,2))
  (xbar - 2)/(sqrt(2)/sqrt(30))
})
plot(density(poisData), main = "Standardized sum of Poisson")
curve(dnorm(x), add = T, col = 2)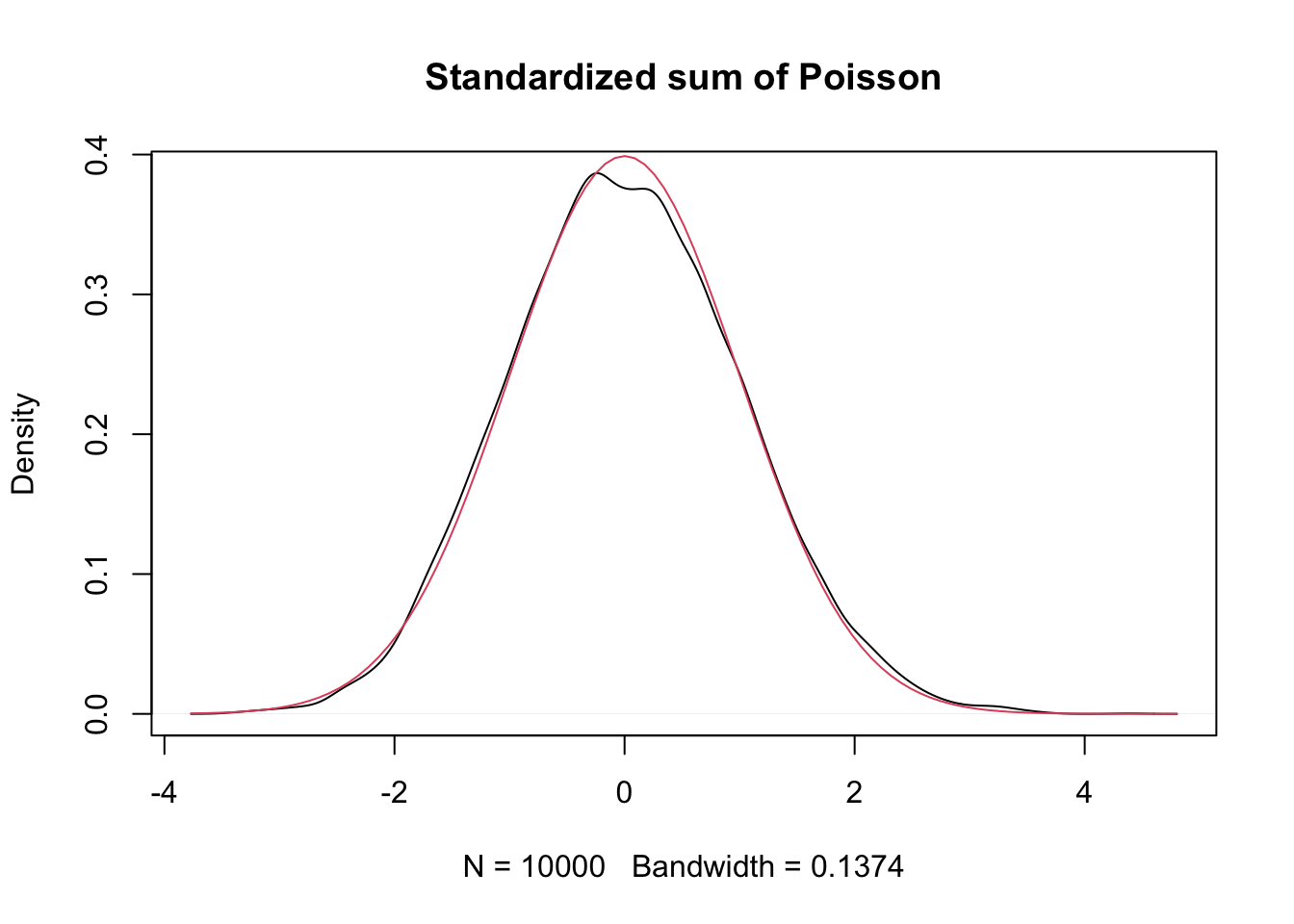

Very close!

Example Let \(X_1,\ldots,X_{50}\) be exponential random variables with rate 1/3. From our knowledge of the exponential distribution, each \(X_i\) has mean \(\mu = 3\) and standard deviation \(\sigma = 3\). The central limit theorem then says that \[ \frac{\overline{X} - 3}{3/\sqrt{50}} \] is approximately normal with mean 0 and standard deviation 1. We check this with a simulation. Again, we can either use histograms or density estimates for this, but this time we choose to use density estimates.

expData <- replicate(10000, {
  dat <- mean(rexp(50,1/3))
  (dat - 3)/(3/sqrt(50))
})
plot(density(expData), main = "Standardized sum of exponentials")
curve(dnorm(x), add = T, col = 2)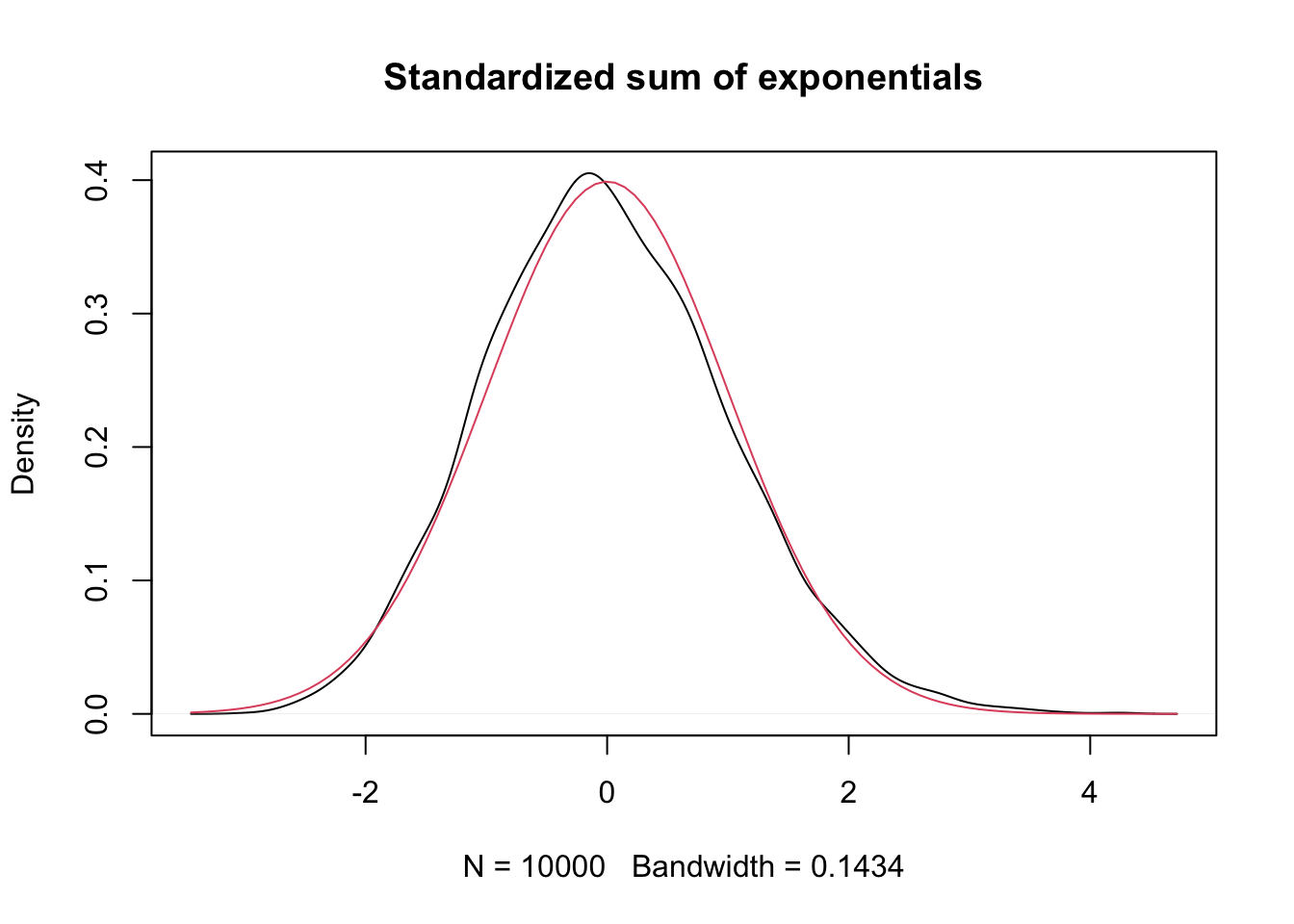

The Central Limit Theorem says that, if you take the mean of a large number of independent samples, then the distribution of that mean will be approximately normal. We call \(\overline{X}\) the sample mean because it is the mean of a random sample. In practice, if the population you are sampling from is symmetric with no outliers, then you can start to see a good approximation to normality after as few as 15-20 samples. If the population is moderately skew, such as exponential or \(\chi^2\), then it can take between 30-50 samples before getting a good approximation. Data with extreme skewness, such as some financial data where most entries are 0, a few are small, and even fewer are extremely large, may not be appropriate for the central limit theorem even with 500 samples (see example below). Finally, there are versions of the central limit theorem available when the \(X_i\) are not iid, but a single outlier of sufficient size invalidates the hypotheses of the Central Limit Theorem, and \(\overline{X}\) will not be normally distributed.

Example A distribution for which sample size of \(n = 500\) is not sufficient for good approximation via normal distributions.

We create a distribution that consists primarily of zeros, but has a few modest sized values and a few large values:

skewdata <- replicate(2000,0)                      # Start with lots of zeros
skewdata <- c(skewdata, rexp(200,1/10))            # Add a few moderately sized values
skewdata <- c(skewdata, seq(100000,500000,50000))  # Add a few large values

mu <- mean(skewdata)
sig <- sd(skewdata)

We use sample to take a random sample of size \(n\) from this distribution. We take the mean, subtract the true mean of the distribution, and divide by \(\sigma/\sqrt{n}\). We replicate that 10000 times. Here are the plots when \(\overline{X}\) is the mean of 100 samples:

n <- 100

skewSample <- replicate(10000, {
  dat <- mean(sample(skewdata, n, TRUE)) 
  (dat - mu)/(sig/sqrt(n))
})
hist(skewSample, probability = T)
curve(dnorm(x), add = T, col = 2)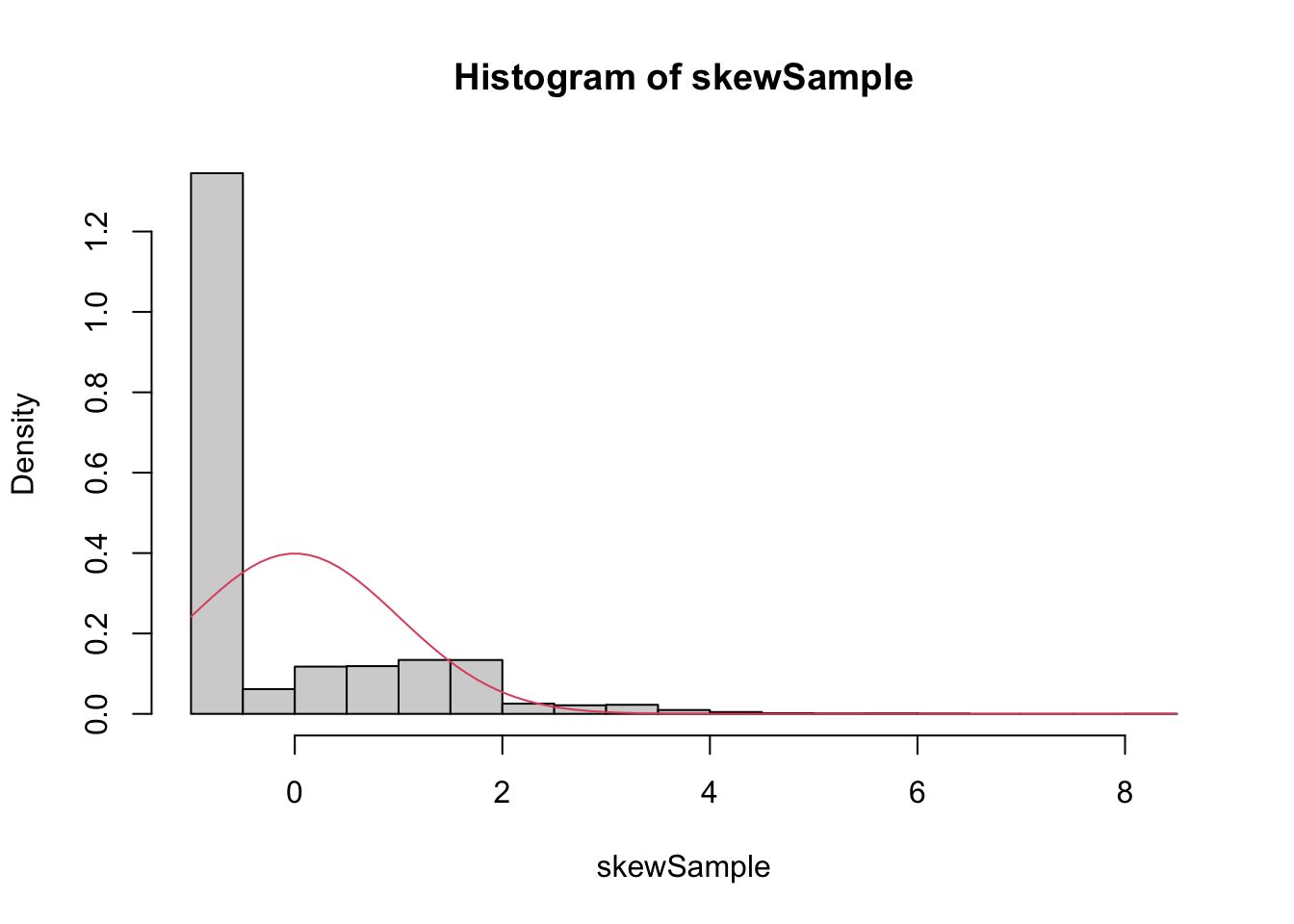

and 500 samples:

n <- 500

skewSample <- replicate(10000, {
  dat <- mean(sample(skewdata, n, TRUE)) 
  (dat - mu)/(sig/sqrt(n))
})

hist(skewSample, probability = T)
curve(dnorm(x), add = T, col = 2)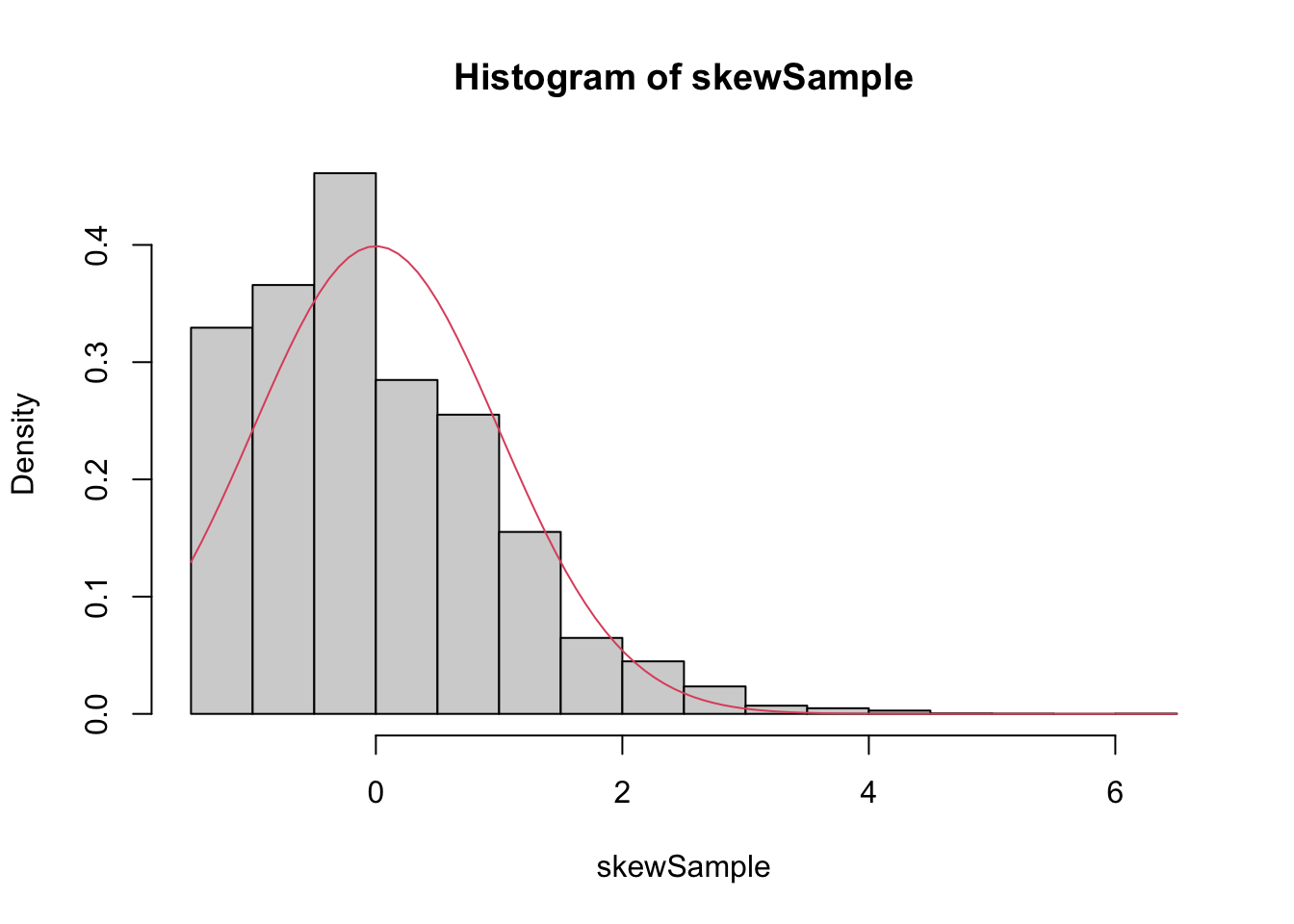

Even at 500 samples, the density is still far from the normal distribution, especially the lack of left tail. Of course, the Central Limit Theorem is still true, so \(\overline{X}\) must become normal if we choose \(n\) large enough:

n <- 5000

skewSample <- replicate(10000, {
  dat <- mean(sample(skewdata, n, TRUE)) 
  (dat - mu)/(sig/sqrt(n))
})

hist(skewSample, probability = T)
curve(dnorm(x), add = T, col = 2)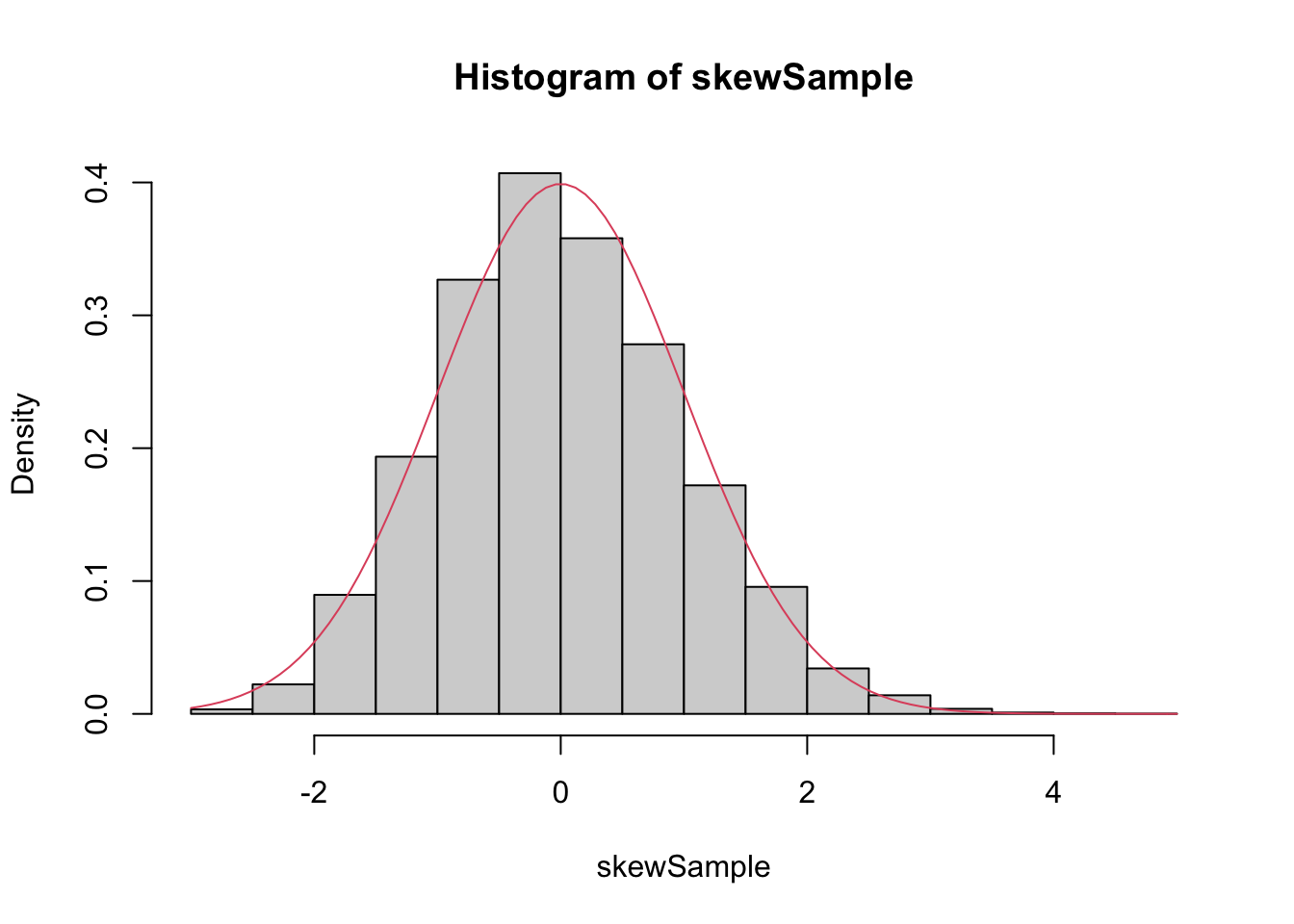

There may still be a slight skewness in this picture, but we are now very close to being normal.

4.6 Sampling Distributions

We describe \(t\), \(\chi^2\) and \(F\) in the context of samples from normal rv. Emphasis is on understanding relationship between the rv and how it comes about from \(\overline{X}\) and \(S\). The goal is for you not to be surprised when we say later that test statistics have certain distributions. You may not be able to prove it, but hopefully won’t be surprised either. We’ll use density estimation extensively to illustrate the relationships.

Given \(X_1,\ldots,X_n\), which we assume in this section are independent and identically distributed with mean \(\mu\) and standard deviation \(\sigma\), we define the sample mean \[ \overline{X} = \sum_{i=1}^n X_i \] and the sample standard deviation \[ S^2 = \frac 1{n-1} \sum_{i=1}^n (X_i - \overline{X})^2 \] We note that \(\overline{X}\) is an estimator for \(\mu\) and \(S\) is an estimator for \(\sigma\).

4.6.1 Linear combination of normal rv’s

Let \(X_1,\ldots,X_n\) be independent rvs with means \(\mu_1,\ldots,\mu_n\) and variances \(\sigma_i^2\). Then \[ E[\sum a_i X_i] = \sum a_i E[X_i] \] and \[ V(\sum a_i X_i) = \sum a_i^2 V(X_i) \] As a consequence, \(E[aX + b] = aE[X] + b\) and \(V(aX + b) = a^2V(X)\). An important special case is that if \(X_1,\ldots,X_n\) are iid with mean \(\mu\) and variance \(\sigma^2\), then \(\overline{X}\) has mean \(\mu\) and variance \(\sigma^2/n\).

In the special case that \(X_1,\ldots, X_n\) are normal random variables, much more can be said. The following theorem generalizes our previous result to sums of more than two random variables.

Theorem 4.4 Let \(X_1,\ldots,X_n\) be independent normal rvs with means \(\mu_1,\ldots,\mu_n\) and variances \(\sigma_1^2,\ldots,\sigma_n^2\). Then, \[ \sum_{i=1}^n a_i X_i \] is normal with mean \(\sum a_i \mu_i\) and variance \(\sum a_i^2 \sigma_i^2\).

You will be asked to verify this via estimating densities in special cases in the exercises. The special case that is very interesting is the following:

Theorem 4.5 Let \(X_1,\ldots,X_n\) be independent identically distributed normal rvs with common mean \(\mu\) and variance \(\sigma^2\). Then \[ \frac{\overline{X} - \mu}{\sigma/\sqrt{n}} \] is standard normal(0,1).

4.6.2 Chi-squared

Let \(Z\) be a standard normal(0,1) random variable. An rv with the same distribution is \(Z^2\) is called a Chi-squared rv with one degree of freedom. The sum of \(n\) independent \(\chi^2\) rv’s with 1 degree of freedom is a chi-squared rv with \(n\) degrees of freedom. In particular, the sum of a \(\chi^2\) with \(\nu_1\) degrees of freedom and a \(\chi^2\) with \(\nu_2\) degrees of freedom is \(\chi^2\) with \(\nu_1 + \nu_2\) degrees of freedom.

We have already seen above that \(Z^2\) has an estimated pdf similar to that of a \(\chi^2\) rv. So, let’s show via estimating pdfs that the sum of a \(\chi^2\) with 2 df and a \(\chi^2\) with 3 df is a \(\chi^2\) with 5 df.

chi2Data <- replicate(10000, rchisq(1,2) + rchisq(1,3))
hist(chi2Data, probability = TRUE)
curve(dchisq(x, df = 5), add = T, col = 2)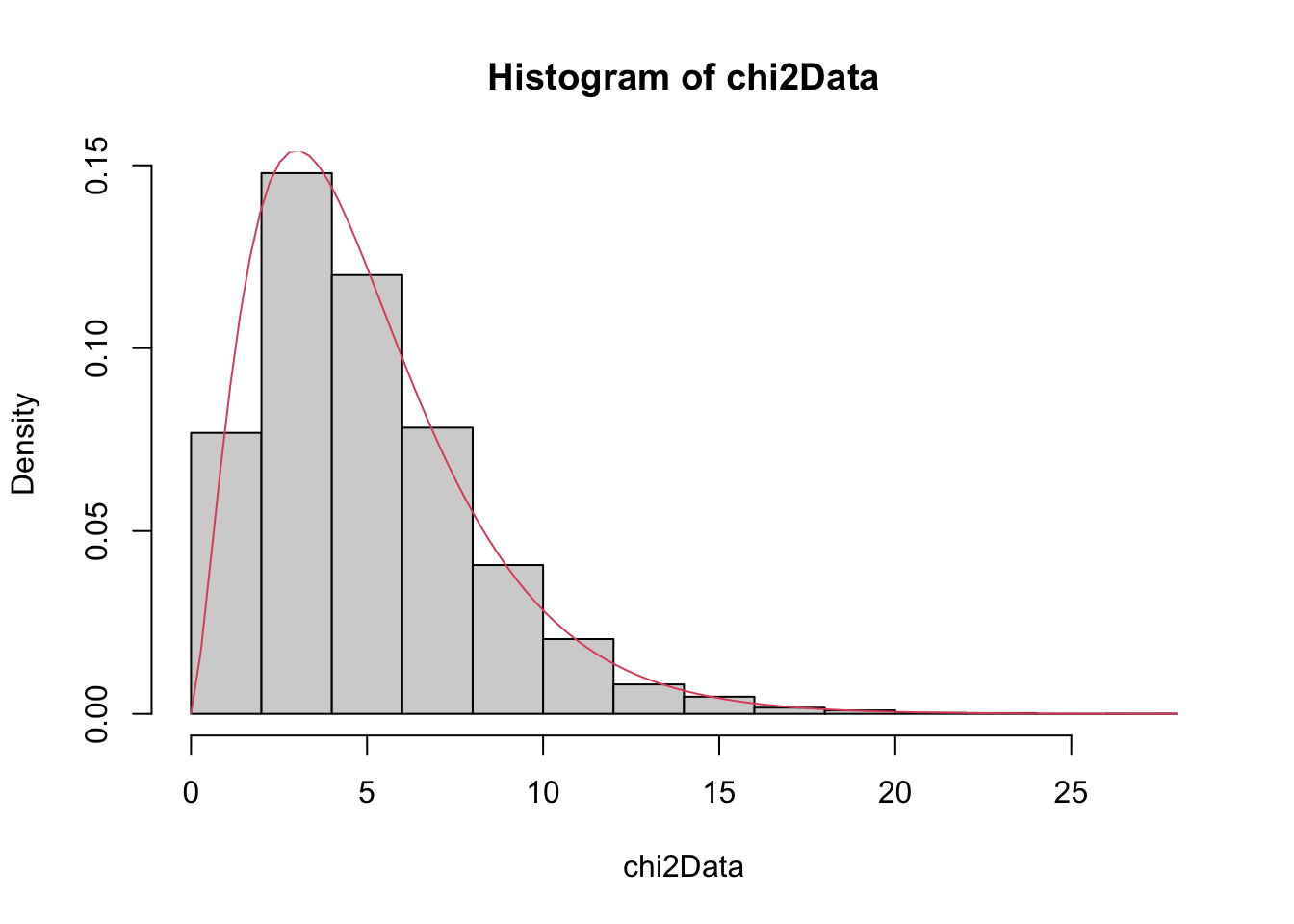

Example If \(X_1,\ldots,X_n\) are iid normal rvs with mean \(\mu\) and standard deviation \(\sigma\), then \[ \frac{n-1}{\sigma^2} S^2 \] is \(\chi^2_{n-1}\).

We provide a heuristic and a simulation as evidence. Heuristic: Note that \[ \frac{n-1}{\sigma^2} S^2 = \frac 1{\sigma^2}\sum_{i=1}^n (X_i - \overline{X})^2 \\ = \sum_{i=1}^n \bigl(\frac{X_i - \overline{X}}{\sigma}\bigr)^2 \] Now, if we had \(\mu\) in place of \(\overline{X}\) in the above equation, we would have exactly a \(\chi^2\) with \(n\) degrees of freedom. Replacing \(\mu\) by its estimate \(\overline{X}\) reduces the degrees of freedom by one, but it remains \(\chi^2\).

For the simulation of this, we estimate the density of \(\frac{n-1}{\sigma^2} S^2\) and compare it to that of a \(\chi^2\) with \(n-1\) degrees of freedom, in the case that \(n = 4\), \(\mu = 3\) and \(\sigma = 9\).

sdData <- replicate(10000, 3/81 * sd(rnorm(4, 3, 9))^2)
hist(sdData, probability = TRUE)
curve(dchisq(x, df = 3), add = T, col = 2)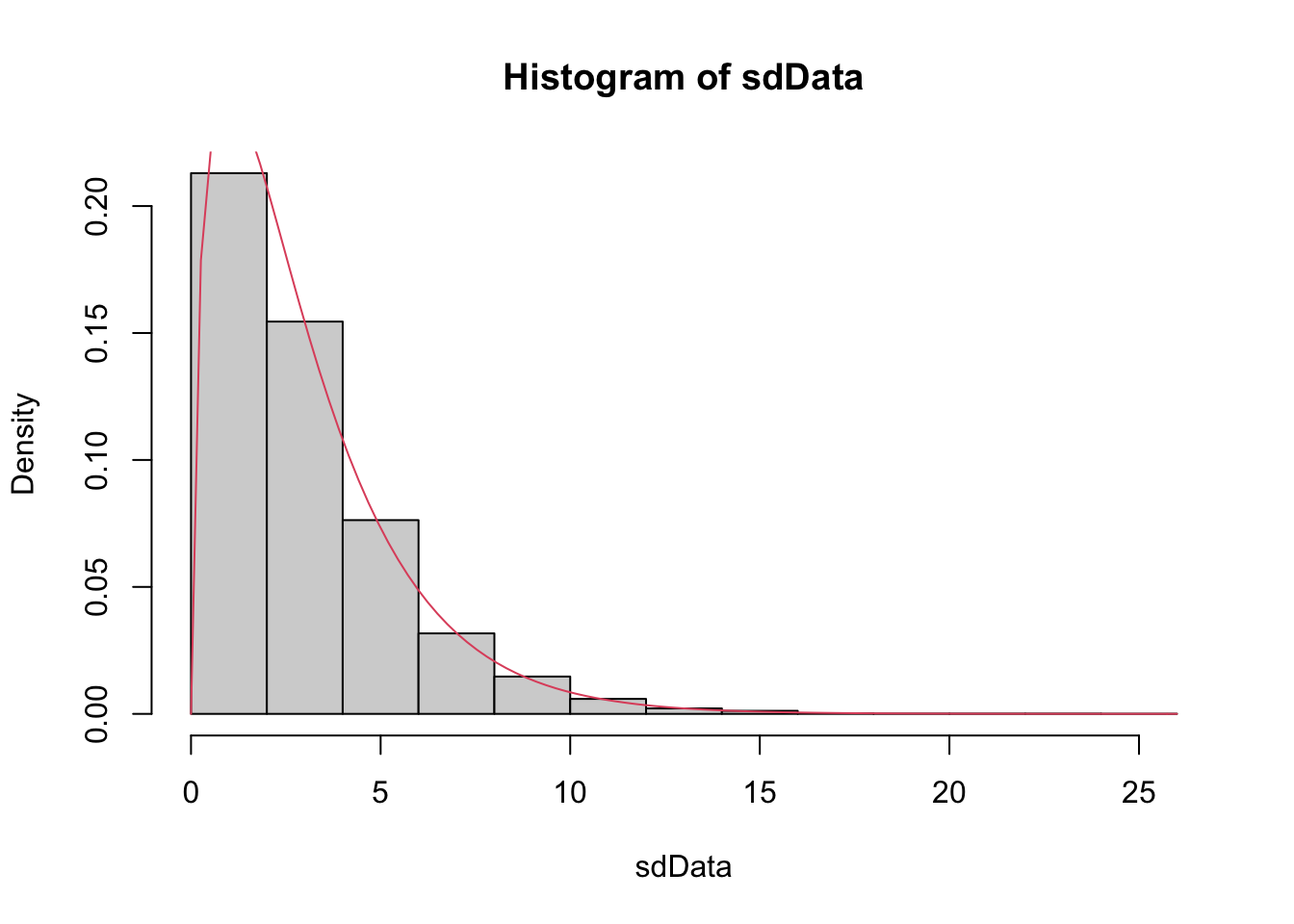

Theorem 4.6 Let \(X_1,\ldots,X_n\) be iid normal random variables. Then, \[ \frac{n-1}{\sigma^2} S^2 \] has a \(\chi^2\) distribution with \(n-1\) degrees of freedom.

4.6.3 The \(t\) distribution

If \(Z\) is a standard normal(0,1) rv, \(\chi^2_\nu\) is a Chi-squared rv with \(\nu\) degrees of freedom, and \(Z\) and \(\chi^2_\nu\) are independent, then

\[ t_\nu = \frac{Z}{\sqrt{\chi^2_\nu/\nu}} \]

is distributed as a \(t\) random variable with \(\nu\) degrees of freedom.

Theorem 4.7 If \(X_1,\ldots,X_n\) are iid normal rvs with mean \(\mu\) and sd \(\sigma\), then \[ \frac{\overline{X} - \mu}{S/\sqrt{n}} \] is \(t\) with \(n-1\) degrees of freedom.

Note that \(\frac{\overline{X} - \mu}{\sigma/\sqrt{n}}\) is normal(0,1). So, replacing \(\sigma\) with \(S\) changes the distribution from normal to \(t\).

Proof: \[ \frac{Z}{\sqrt{\chi^2_{n-1}/n}} = \frac{\overline{X} - \mu}{\sigma/\sqrt{n}}*\sqrt{\frac{\sigma^2 (n-1)}{S^2(n-1)}}\\ = \frac{\overline{X} - \mu}{S/\sqrt{n}} \] Where we have used that \((n - 1) S^2/\sigma^2\) is \(\chi^2\) with \(n - 1\) degrees of freedom.

Example Estimate the pdf of \(\frac{\overline{X} - \mu}{S/\sqrt{n}}\) in the case that \(X_1,\ldots,X_6\) are iid normal with mean 3 and standard deviation 4, and compare it to the pdf of the appropriate \(t\) random variable.

tData <- replicate(10000, {
  normData <- rnorm(6,3,4)
  (mean(normData) - 3)/(sd(normData)/sqrt(6))
}) 
hist(tData, probability = TRUE)
curve(dt(x, df = 5), add = TRUE, col = 2)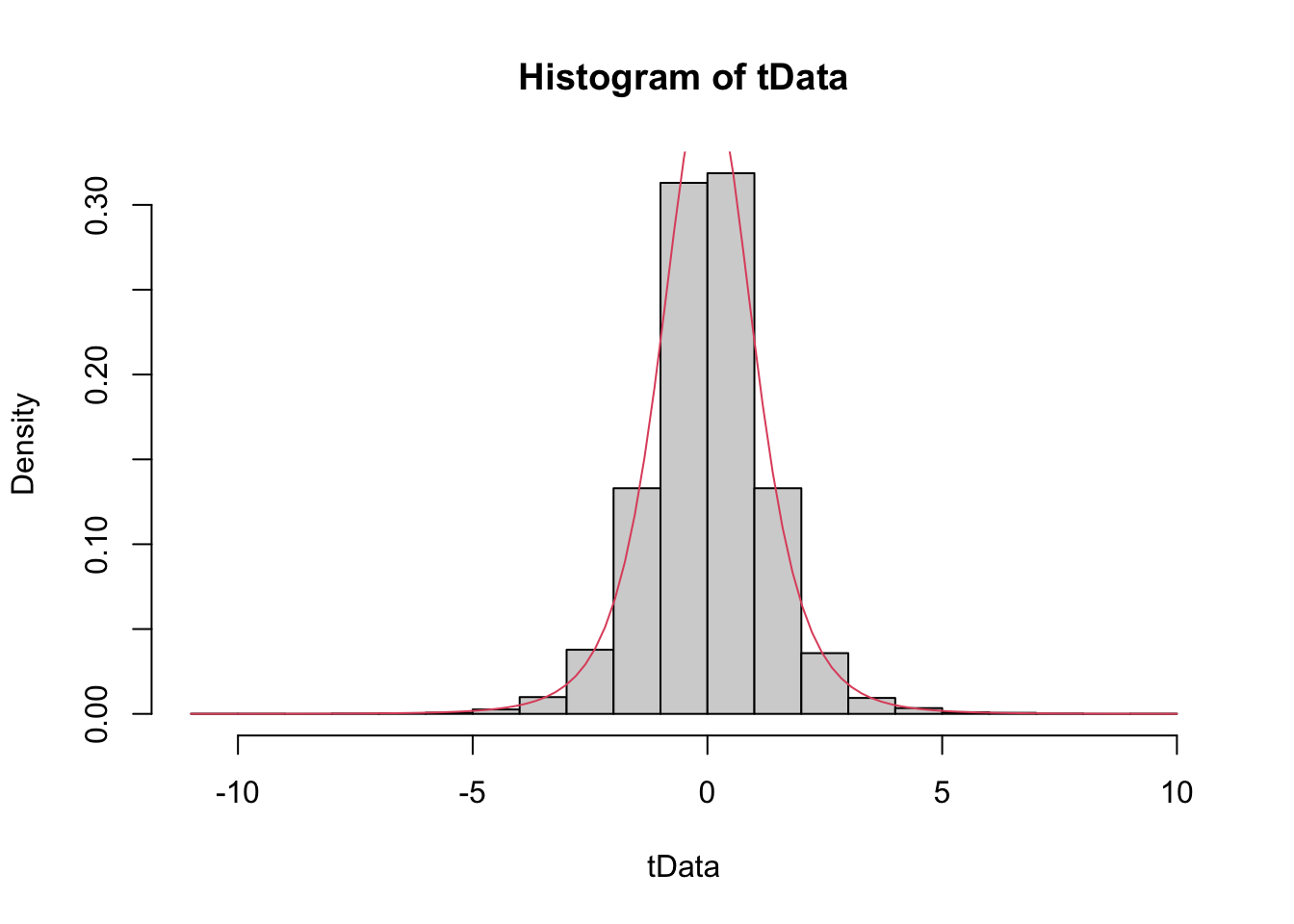

We see a very good correlation.

4.6.4 The F distribution

An \(F\) distribution has the same density function as \[ F_{\nu_1, \nu_2} = \frac{\chi^2_{\nu_1}/\nu_1}{\chi^2_{\nu_2}/\nu_2} \] We say \(F\) has \(\nu_1\) numerator degrees of freedom and \(\nu_2\) denominator degrees of freedom.

One example of this type is: \[ \frac{S_1^2/\sigma_1^2}{S_2^2/\sigma_2^2} \] where \(X_1,\ldots,X_{n_1}\) are iid normal with standard deviation \(\sigma_1\) and \(Y_1,\ldots,Y_{n_2}\) are iid normal with standard deviation \(\sigma_2.\)

4.6.5 Summary

\(aX+ b\) is normal with mean \(a\mu + b\) and standard deviation \(a\sigma\) if \(X\) is normal with mean \(\mu\) and sd \(\sigma\).
\(\frac{X - \mu}{\sigma}\sim Z\) if \(X\) is Normal(\(\mu, \sigma\)).
\(\frac{\overline{X} - \mu}{\sigma/\sqrt{n}} \sim Z\) if \(X_1,\ldots,X_n\) iid normal(\(\mu, \sigma\))
\(\lim_{n\to \infty} \frac{\overline{X} - \mu}{\sigma/\sqrt{n}} \sim Z\) if \(X_1,\ldots,X_n\) iid with finite variance.
\(Z^2 \sim \chi^2_1\)
\(\chi^2_\nu + \chi^2_\eta \sim \chi^2_{\nu + \eta}\)
\(\frac{(n-1)S^2}{\sigma^2} \sim \chi^2_{n-1}\) when \(X_1,\ldots,X_n\) iid normal.
\(\frac Z{\sqrt{\chi^2_\nu/\nu}} \sim t_\nu\)
\(\frac{\overline{X} - \mu}{S/\sqrt{n}}\sim t_{n-1}\) when \(X_1,\ldots,X_n\) iid normal.
\(\frac{\chi^2_\nu/\nu}{\chi^2_\mu/\mu} \sim F_{\nu, \mu}\)
\(\frac{S_1^2/\sigma_1^2}{S_2^2/\sigma_2^2} \sim F_{n_1 - 1, n_2 - 1}\) if \(X_1,\ldots,X_{n_1}\) iid normal with sd \(\sigma_1\) and \(Y_1,\ldots,Y_{n_2}\) iid normal with sd \(\sigma_2\).

4.7 Point Estimators

This section gives a brief overview of point estimators.

If \(X\) is a random variable that depends on parameter \(\beta\), then often we are interested in estimating the value of \(\beta\) from a random sample \(X_1,\ldots,X_n\) from \(X\). For example, if \(X\) is a normal rv with unknown mean \(\mu\), and we get data \(X_1,\ldots, X_n\), it would be very natural to estimate \(\mu\) by \(\frac 1n \sum_{i=1}^n X_i\). Notationally, we say \[ \hat \mu = \frac 1n \sum_{i=1}^n X_i = \overline{X} \] In other words, our estimate of \(\beta\) from the data \(x_1,\ldots, x_n\) is denoted by \(\hat \beta\).

The two point estimators that we are interested in at this point are point estimators for the \(mean\) of an rv and the \(variance\) of an rv. (Note that we have switched gears a little bit, because the mean and variance aren’t necessarily parameters of the rv. We are really estimating functions of the parameters at this point. The distinction will not be important for the purposes of this text.) Recall that the definition of the mean of a discrete rv with possible values \(x_i\) is \[ E[X] = \mu = \sum_{i=1}^n x_i p(x_i) \] If we are given data \(x_1,\ldots,x_n\), it is natural to assign \(p(x_i) = 1/n\) for each of those data points to create a new random variable \(X_0\), and we obtain \[ E[X_0] = \frac 1n \sum_{i=1}^n x_i = \overline{x} \] This is a natural choice for our point estimator for the mean of the rv \(X\), as well. \[ \hat \mu = \overline{x} = \frac 1n \sum_{i=1}^n x_i \]

Continuing in the same way, if we are given data \(x_1,\ldots,x_n\) and we wish to estimate the variance, then we could create a new random variable \(X_0\) whose possible outcomes are \(x_1,\ldots,x_n\) with probabilities \(1/n\), and compute \[ \sigma^2 = E[(X- \mu)^2] = \frac 1n \sum_{i=1}^n (x_i - \mu)^2 \] This works just fine as long as \(\mu\) is known. However, most of the time, we do not know \(\mu\) and we must replace the true value of \(\mu\) with our estimate from the data. There is a heuristic that each time you replace a parameter with an estimate of that parameter, you divide by one less. Following that heuristic, we obtain \[ \hat \sigma^2 = S^2 = \frac 1{n-1} \sum_{i=1}^n (x_i - \overline{x})^2 \]

4.7.1 Properties of Point Estimators

Note that the point estimators for \(\mu\) and \(\sigma^2\) can be thought of as random variables themselves, since they are combinations of a random sample from a distribution. As such, they also have distributions, means and variances. One property of point estimators that is often desirable is that it is unbiased. We say that a point estimator \(\hat \beta\) for \(\beta\) is unbiased if \(E[\hat \beta] = \beta\). (Recall: \(\hat \beta\) is a random variable, so we can take its expected value!) Intuitively, unbiased means that the estimator does not consistently underestimate or overestimate the parameter it is estimating. If were to estimate the parameter over and over again, the average value would converge to the correct value of the parameter.

Let’s consider \(\overline{x}\) and \(S^2\). Are they unbiased? It is possible to determine this analytically, and interested students should consult Wackerly et al for a proof. However, we will do this using R and simulation.

Example

Let \(X_1,\ldots, X_{5}\) be a random sample from a normal distribution with mean 1 and variance 1. Compute \(\overline{x}\) based on the random sample.

mean(rnorm(5,1,1))

## [1] 1.614421

You can see the estimate is pretty close to the correct value of 1, but not exactly 1. However, if we repeat this experiment 10,000 times and take the average value of \(\overline{x}\), that should be very close to 1.

mean(replicate(10000, mean(rnorm(5,1,1))))

## [1] 1.003684

It can be useful to repeat this a few times to see whether it seems to be consistently overestimating or underestimating the mean. In this case, it is not.

Variance

Let \(X_1,\ldots,X_5\) be a random sample from a normal rv with mean 1 and variance 4. Estimate the variance using \(S^2\).

sd(rnorm(5,1,2))^2

## [1] 5.398046

We see that our estimate is not ridiculous, but not the best either. Let’s repeat this 10,000 times and take the average. (We are estimating \(E[S^2]\).)

mean(replicate(10000, sd(rnorm(5,1,2))^2))

## [1] 3.986978

Again, repeating this a few times, it seems that we are neither overestimating nor underestimating the value of the variance.

For the sake of completeness, let’s show that \(\frac 1n \sum_{i=1}^n (x_i - \overline{x})^2\) is biased.

mean(replicate(10000, {
  data = rnorm(5,1,2) 
  1/5*sum((data - mean(data))^2)
}))

## [1] 3.253624

If you run the above code several times, you will see that \(\frac 1n \sum_{i=1}^n (x_i - \overline{x})^2\) tends to significantly underestimate the value of \(\sigma^2 = 4\).

4.7.2 Variance of Unbiased Estimators

From the above, we can see that \(\overline{x}\) and \(S^2\) are unbiased estimators for \(\mu\) and \(\sigma^2\), respectively. There are other unbiased estimator for the mean and variance, however. For example, if \(X_1,\ldots,X_n\) is a random sample from a normal rv, then the median of the \(X_i\) is also an unbiased estimator for the mean. Moreover, the median seems like a perfectly reasonable thing to use to estimate \(\mu\), and in many cases is actually preferred to the mean. There is one way, however, in which the sample mean \(\overline{x}\) is definitely better than the median, and that is that it has a lower variance. So, in theory at least, \(\overline{x}\) should not deviate from the true mean as much as the median will deviate from the true mean, as measured by variance.

Let’s do a simulation to illustrate. Suppose you have a random sample of size 11 from a normal rv with mean 0 and standard deviation 1. We estimate the variance of \(\overline{x}\).

sd(replicate(10000, mean(rnorm(11,0,1))))^2

## [1] 0.08955216

Now we repeat for the median.

sd(replicate(10000, median(rnorm(11,0,1))))^2

## [1] 0.1381326

And, we see that the variance of the mean is lower than the variance of the median. This is a good reason to use the sample mean to estimate the mean of a normal rv rather than using the median, absent other considerations such as outliers.

Exercises

Five coins are tossed and the number of heads \(X\) is counted. Estimate via simulation the pmf of \(X\).
Consider an experiment where 20 balls are placed randomly into 10 urns. Let \(X\) denote the number of urns that are empty.
1. Estimate via simulation the pmf of \(X\).
2. What is the most likely outcome?
3. What is the least likely outcome that has positive probability?
(Hard) Suppose 6 people, numbered 1-6, are sitting at a round dinner table with a big plate of spaghetti, and a bag containing 5005 red marbles and 5000 blue marbles. Person 1 takes the spaghetti, serves themselves, and chooses a marble. If the marble is red, they pass the spaghetti to the left. If it is blue, they pass the spaghetti to the right. The guests continue doing this until the last person receives the plate of spaghetti. Let \(X\) denote the number of the person holding the spaghetti at the end of the experiment. Estimate the pmf of \(X\).
Recall the example in the text, where we show that the most likely number of times you have more Heads than Tails when a coin is tossed 100 times is zero. Suppose you toss a coin 100 times.
1. Let \(X\) be the number of times in the 100 tosses that you have exactly the same number of Heads as Tails. Estimate the expected value of \(X\).
2. Let \(Y\) be the number of tosses for which you have more Heads than Tails. Estimate the expected value of \(Y\).
Let \(X\) and \(Y\) be uniform random variables on the interval \([0,1]\). Plot the pdf of \(X+Y\).
Let \(X\) and \(Y\) be uniform random variables on the interval \([0,1]\). Let \(Z\) be the maximum of \(X\) and \(Y\).
1. Plot the pdf of \(Z\).
2. From your answer to (a), decide whether \(P(0 \le Z \le 1/3)\) or \(P(1/3\le Z \le 2/3)\) is larger.
Is the product of two normal rvs normal? Estimate via simulation the pdf of the product of \(X\) and \(Y\), when \(X\) and \(Y\) are normal random variables with mean 0 and standard deviation 1. How can you determine whether \(XY\) is normal? Hint: you will need to estimate the mean and standard deviation.
Consider the Log Normal distribution, whose root in R is lnorm. The log normal distribution takes two parameters, meanlog and sdlog.
1. Graph the pdf of a Log Normal random variable with meanlog = 0 and sdlog = 1. The pdf of a Log Normal rv is given by dlnorm(x, meanlog, sdlog).
2. Let \(X\) be a log normal rv with meanlog = 0 and sdlog = 1. Estimate via simulation the density of \(\log(X)\), and compare it to a standard normal random variable.
3. Estimate the mean and standard deviation of a Log Normal random variable with parameters 0 and 1/2.
4. Using your answer from (b), find an integer \(n\) such that \[ \frac{\overline{X} - \mu}{\sigma/\sqrt{n}} \] is approximately normal with mean 0 and standard deviation 1.
Let \(X_1,\ldots,X_{n}\) be uniform rv’s on the interval \((0,1)\). How large does \(n\) need to be before the pdf of \(\frac{\overline{X} - \mu}{\sigma/\sqrt{n}}\) is approximately that of a standard normal rv? (Note: there is no “right” answer, as it depends on what is meant by “approximately.” You should try various values of \(n\) until you find one where the estimate of the pdf is close to that of a standard normal.)
Let \(X_1,\ldots,X_{n}\) be chi-squared rv’s with 2 degrees of freedom. How large does \(n\) need to be before the pdf of \(\frac{\overline{X} - \mu}{\sigma/\sqrt{n}}\) is approximately that of a standard normal rv? (Hint: the wiki page on chi-squared will tell you the mean and sd of chi-squared rvs.)
The sum of two independent chi-squared rv’s with 2 degrees of freedom is either exponential or chi-squared. Which one is it? What is the parameter associated with your answer?
The minimum of two exponential rv’s with mean 2 is an exponential rv. Use simulation to determine what the rate is.
Estimate the value of \(a\) such that \(P(a \le Y \le a + 1)\) is maximized when \(Y\) is the maximum value of two exponential random variables with mean 2.
Let \(X\) and \(Y\) be independent uniform rvs on the interval \([0,1]\). Estimate via simulation the pdf of the maximum of \(X\) and \(Y\), and compare it to the pdf of a beta distribution with parameters shape1 = 2 and shape2 = 1. (Use dbeta().)
Estimate the density of the maximum of 7 uniform random variables on the interval \([0,1]\). This density is also beta; what are the parameters for the beta distribution?
Determine whether \(\frac 1n \sum_{i=1}^n (x_i - \mu)^2\) is a biased estimator for \(\sigma^2\) when \(n = 10\), \(x_1,\ldots,x_{10}\) is a random sample from a normal rv with mean 1 and variance 9.
Show through simulation that \(S^2 = \frac {1}{n-1} \sum_{i=1}^n \bigl(x_i - \overline{x}\bigr)^2\) is an unbiased estimator for \(\sigma^2\) when \(x_1,\ldots, x_{10}\) are iid normal rv’s with mean 0 and variance 4.
Show through simulation that \(S = \sqrt{S^2}\), where \(S\) is defined in the previous problem, is a biased estimator for \(\sigma\) when \(x_1,\ldots,x_{10}\) are iid normal random variables with mean 0 and variance 4, i.e. standard deviation 2.
Show through simulation that the median is an unbiased estimator for the mean of a normal rv with mean 1 and standard deviation 4. Assume a random sample of size 8.
Suppose you roll a die until the first time you obtain an even number. Let \(X_1\) be the total number of times you roll a 1, and let \(X_2\) be the total number of times that you roll a 2.
1. Is \(E[X_1] = E[X_2]\)? (Hint: Use simulation. It is extremely unlikely that you will roll 30 times before getting the first even number, so you can safely assume that the first even occurs inside of 30 rolls.)
2. Is the pmf of \(X_1\) the same as the pmf of \(X_2\)?
3. Estimate the variances of \(X_1\) and \(X_2\).
(Requires programming skills beyond what is covered in the text) Deathrolling in World of Warcraft works as follows. Player 1 tosses a 1000 sided die. Say they get \(x_1\). Then player 2 tosses a die with \(x_1\) sides on it. Say they get \(x_2\). Player 1 tosses a die with \(x_2\) sides on it. The player who loses is the player who first rolls a 1.
1. Estimate the expected total number of rolls before a player loses.
2. Estimate the probability mass function of the total number of rolls.
3. Estimate the probability that player 1 wins.

count(data.frame(x = replicate(10000, {birthdays <- sample(1:365, 50, replace = TRUE); sum(table(birthdays)[table(birthdays) > 1]) })), x) %>% mutate(prop = n/10000) %>% ggplot(aes(x, prop)) + geom_bar(stat = "identity")↩︎